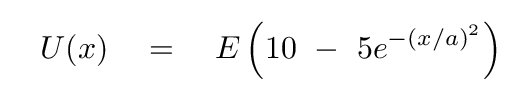
where
- E = 6 x 10-11 Joules
- a = 3.5 x 10-4 meters is the diameter of the tip of a frayed wire
- Is the position x = 0 a stable equilibrium for the dust speck?
- If the dust speck is displaced slightly from x = 0, show that it will exhibit simple harmonic motion.
- What will the frequency of this motion be?
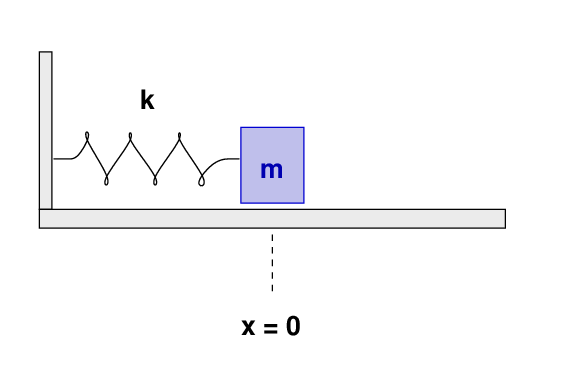
A block of mass m sits on a frictionless surface, inside a vacuum chamber. It is attached to an ideal spring of force constant k, such that it sits at rest at position x = 0.
The block is displaced a small distance x from the equilibrium point.
- Write an equation for the net force on the block in the x-direction.
- Write a differential equation governing the motion of the block in the x-direction.
- Draw a graph showing position as a function of time.
Air is now added to the chamber, which causes the block to encounter an air resistance force as it moves, Fair = -bv, where v is the velocity of the block.
Suppose that, once again, the block is moved a distance x away from its equlibrium position and released.
- Write an equation for the net force on the block in the x-direction.
- Write a differential equation governing the motion of the block in the x-direction.
- As more air is added, the value of b increases. What value of b will cause the block to come to rest in the minimum time?
- Draw a graph showing position as a function of time for this value of b
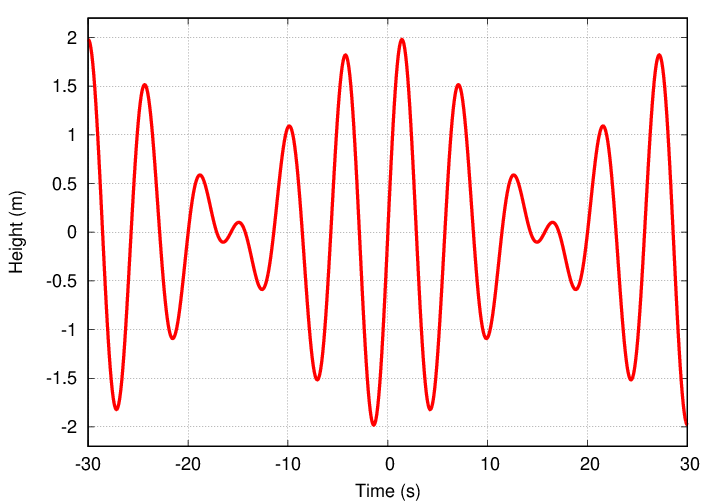
Earthquake! The ground ripples and rolls. Videos of the freeway show a change in the height of the roadway over time, recorded in the figure above.
Geologists determine that this disturbance was the sum of two pure sinusoidal waves, which had roughly equal amplitudes. Each wave travelled along the highway at a speed of v = 50 m/s.
- What were the frequencies of the two waves?
The highway's surface is made of gravel and asphalt, with a depth of 0.5 m and an average density of ρ = 4000 kg/m3. Each of the 4 lanes (2 going north, 2 going south) is about 5 m wide.
- Estimate the power transmitted to the road surface by the earthquake waves.
Fred creates a primitive musical instrument by hanging a steel cauldron of mass M = 10 kg from a wire of mass m = 0.02 kg and length L = 2 m. To play the instrument, Fred pulls the middle of the wire d = 5 mm to the left, then releases it. The wire oscillates back and forth in its fundamental mode, making a low hum.
- What is the frequency of this sound?
- How hard must Fred pull the wire horizontally?
Leopold is not impressed. He demands that Fred play a note with a frequency which is exactly 1.5 times higher. "That's not possible," explains Fred. "Then MAKE it possible!" exclaims Leopold.
Fred looks around. All he sees is a big pile of sand, and a pair of pliers.
- Explain exactly what Fred would need to do to satisfy Leopold, using ONLY the sand.
- Explain exactly what Fred would need to do to satisfy Leopold, using ONLY the pliers.
A certain type of oil has an index of refraction given by
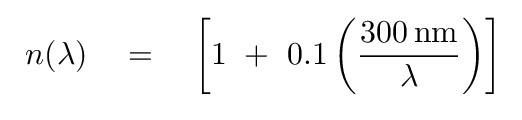
Light rays produced by distant lasers travel through a vacuum, toward a tank of this oil. The wavelengths of these waves, in a vacuum, are
- from source 1: 400 nm
- from source 2: 600 nm
- What is the angular frequency of each set of waves?
The waves enter the oil, and, for a short distance, they interfere as they travel together in the same direction.
- What is the wavelength of each set of waves, in the oil?
- What is the wave number of each set of waves, in the oil?
- What is the group velocity of the combined waves in the oil?
- What is the phase velocity of the combined waves in the oil?
I have a long, thin rod of copper, of length L. I hold it firmly between thumb and finger at a spot one-quarter of the way from left to right, and then tap a small hammer against the right end of the rod.
I hear, very faintly, a high-pitched ringing sound. Leopold exclaims, "Mon Dieu! Exactly five octaves above middle C!"
How long is the rod?