
Table 1 taken from Ferriere, K. M., Reviews of Modern Physics, 73, 1031 (2001)
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Today, we'll move from the cold atomic (HI) phase of the ISM to the cold molecular (H2) phase.

Table 1 taken from
Ferriere, K. M., Reviews of Modern Physics, 73, 1031 (2001)
As you will see shortly, clouds of gas in molecular form aren't just hydrogen; there are a number of heavier elements which play important roles in their creation. Sometimes, the trace elements can help us to study the clouds; other times, they just get in our way.
So, let's review the abundances of the elements in space. There are variations from place to place, and from long ago until recent times, but the graph below, based on observations in the Solar System, provides a useful general guide. Pay special attention to the labels on the Y-axis.
If that pattern of even-high/odd-low really bothers you,
you can learn more about
the Oddo-Harkins rule
on your own.
Clouds of cold atomic hydrogen are easy to find,
since the atoms emit radio waves at a wavelength
of 21 cm due to the hyperfine transition in the ground state.
What about cold molecular hydrogen gas?
What sort of radiation does it emit?
Alas, molecules of hydrogen do not radiate electromagnetic
energy very efficiently.
The problem is that the coupling between a molecule
and the electromagnetic field --
which determines the probability that photons will be
absorbed or emitted by the molecule --
depends in large part on the electric dipole moment
of the molecule.
The stronger the dipole moment, the more strongly
the molecule interacts with electromagnetic radiation.
Molecular hydrogen consists of two identical atoms joined together,
yielding no electric dipole moment at all.
The combination does have a quadrupole moment,
but that yields only weak coupling to photons.
In order to detect clouds of molecular gas, we need to look
for OTHER molecules,
preferably those which
Among the best options are
though radio astronomers have
found many others
(thanks to
Karen Lee-Waddell's ICRAR/CASS Radio School 2018 presentation.)
We will concentrate on the carbon monoxide molecule for
the rest of today's discussion.
Inside clouds of molecular gas,
the temperatures are very low, only 10 - 20 Kelvin.
That means that only transitions between very low energy states
are likely to produce significant amounts of radiation.
Instead of considering the
electronic energy states of these molecules,
we should instead examine the
vibrational
and
rotational
energy states.
Let's start with VIBRATIONAL modes.
You should remember the example of a block attached
to a spring, sliding along a frictionless floor.
If one pulls the block away from its rest position,
it will start to oscillate back and forth
in Simple Harmonic Motion (SHM).
The mass m of the block and the force constant k
of the spring, of course.
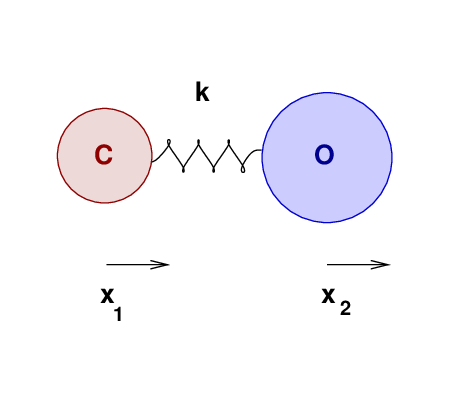
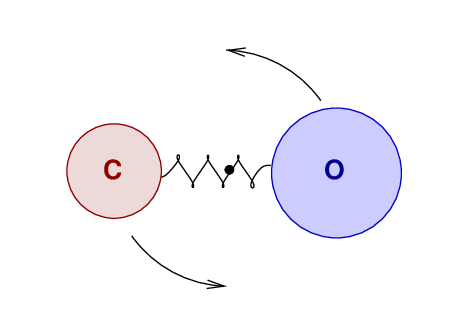
One can build a similar model of a CO molecule as two
masses attached by a spring:
Once again, the modes of vibration depend on mass
(in this case, the masses of both atoms)
and the size of the force
(between the two atoms).
However, unlike the everyday block and spring,
this molecule can oscillate at a number of different frequencies.
A quantum mechanical analysis shows that
the allowed frequencies follow a simple pattern
(at least for the lowest energy states,
which are the relevant ones inside a molecular cloud).
The corresponding vibrational energies of the molecule
are
In the case of CO,
the combination ℏω0
is equal to
0.269 eV.
One of the strongest lines emitted by the molecule
involves a transition from
the vibrational state n = 1 to the ground state n = 0.
There is a second way that molecules can produce
(or absorb) electromagnetic radiation:
by making transitions between ROTATIONAL states.
Just as the vibrational states of these molecules
are quantized,
so are their rotational states:
molecules may only have specific values of rotational angular momentum.
As a result, their rotational energies are also quantized.
One can express these rotational energy states as
where J is the rotational quantum number
and I the moment of inertia.
It is common to replace the ℏ/2I term
with a single constant B0 for convenience,
yielding
One can look up the rotational energy constant B0
for any particular molecule of interest.
In the case of CO,
it has value
B0 = 2.3825 x 10-4 eV.
In the case of rotational transitions,
quantum mechanical rules require that the rotational index J
changes by one;
in other words,
J → J ± 1.
Radio astronomers have adopted CO as a tracer
of molecular hydrogen:
if they detect CO in some region of space, they can assume safely
that molecular hydrogen is there, too.
But because both carbon and oxygen are less common in the ISM
than hydrogen,
the number of
H2 molecules
will greatly exceed that of CO.
As a rough guide,
one can expect roughly
20,000 molecules of H2 for every single CO.
One might think that since hydrogen atoms are by far the
most common denizens of space,
the creation of hydrogen molecules would be a simple matter:
whenever two H atoms bump into each other,
they stick together and *poof* an H2 molecule is formed.
Alas, no. The probability that two H atoms will actually
combine during a collision is very, very, very small.
While this can happen, and was the mechanism for creating
molecular gas in the very early universe,
it's just too slow to be important in the contemporary Milky Way.
Instead, the dominant mechanism for the creation of molecular hydrogen
involves a catalyst:
dust grains.
The basic idea is that
a grain provides a place for hydrogen atoms to meet and form pairs --
sort of like a celestial singles bar.
The sequence of events runs like so:
One of the reasons that this process is so efficient is that,
under typical conditions in a molecular cloud,
collisions between dust grains and H atoms are pretty frequent,
providing many opportunities for molecules to form.
How frequent are the collisions?
Let's do a quick estimate.
In a typical atomic cloud, the gas has
Dust grains (which we will discuss in detail shortly) have a wide range
of properties, but a representative grain might have a radius
of about a = 0.1 micron = 10-7 m.
We'll talk more about dust in a week or two,
so for now, I'll just provide a clue on the origin
of all the dust in space.
All the elements heavier than hydrogen are created by fusion
in the cores of stars --
so how do those elements end up in space, between the stars?
In the late stages of evolution,
material from the core of a star can be
dredged up
into the gaseous envelope.
Some stars, especially the blue and red supergiants,
can then shed large amounts of dust (and gas) in
stellar winds.
The picture below shows the star
HD 96548,
which
(according to
Ignace, R., et all., MNRAS 519, 3271 (2023))
has a mass 28 times larger than the Sun
and is ejecting about 6 x 10-5 solar masses of gas
each year from its outer layers.
In the dense blobs of this enriched gas,
atoms of heavy elements can run into each other and stick
together to form molecules and, eventually, dust grains.
Some stars, in the last stages of their giant phases,
eject nearly their entire gaseous outer envelopes into space;
the resulting shells of gas (and dust), energized by
photons from the very hot white-dwarf remnant of the star,
glow as beautiful planetary nebulae.
This is the famous
Ring Nebula,
in an optical image taken with the Hubble Space Telescope.
This infrared image of Ring Nebula,
taken with the
MIRI instrument on JWST,
shows locations where the ejected gas has run into
interstellar material,
creating dense filaments which facilitate the production of dust grains.
Of course, on those rare occasions when a massive star
simply explodes as a
supernova,
all of the material inside,
hydrogen, helium, plus all the heavier elements built up in the core,
are spewed out into space at very high speeds.
The image below shows an X-ray view of the
supernova remnant known as "G292.0+1.8".
The explosion of this star created quite a large amount
of "metals" which, in the future, may turn into grains
of dust.
In the table below, the second column provides the total
amount of heavy elements ejected into space,
in units of solar masses.
Now that we know where
H2
can be formed,
we need to worry about how, and where, it might be destroyed.
Interstellar space contains both
cold atomic and cold molecular gas --
the relative rates of creation and destruction
determine the fraction of hydrogen in each form.
There are two main mechanisms for breaking
a molecule of hydrogen back into two independent atoms.
In typical interstellar conditions,
the second mechanism is by far more important.
Just how much energy does a photon need in order to
dissociate
H2?
The answer is a bit tricky.
As
Ryden and Pogge (2021)
explain,
while a photon of energy
roughly 4.5 eV should be able to excite
a molecule into a vibrational state which can un-bind it,
the absorption of such a photon is very unlikely,
due to the lack of an electric dipole moment.
On the other hand,
photons with energies greater than 11.1 eV
interact more strongly with the molecule,
and they can also lead to its destruction.
That critical photon energy of
is just a bit smaller than another important
energy in the ISM:
the energy to ionize a hydrogen atom from its ground state.
That energy should be familiar to you:
What will happen if a cloud of gas
containing both atomic and molecular hydrogen is exposed
to high-energy photons?
Most radiation sources produce a larger number of low-energy photons,
so, in most cases,
the molecular hydrogen will be more affected more strongly.
In the outermost layers of gas,
molecular hydrogen will break up into two neutral atoms,
and atomic hydrogen may be ionized.
Eventually,
the atomic gas forms a "shield" that prevents high-energy
photons from reaching the inner regions of the cloud.
The end result is that cold molecular clouds exposed
to high-energy photons form a set of layers near their surfaces:
Astronomers call these interfaces between cold, molecular
gas and a source of high-energy photons
dissociation regions
One nearby example can be found in the Orion Nebula,
in the "bar" at lower-left:
It might seem a bit strange to find a cluster of hot, young stars
so close to a cloud of very cold gas ...
but, as we will see next time,
clouds of molecular hydrogen give birth to most, if not all,
of the stars in the Galaxy.
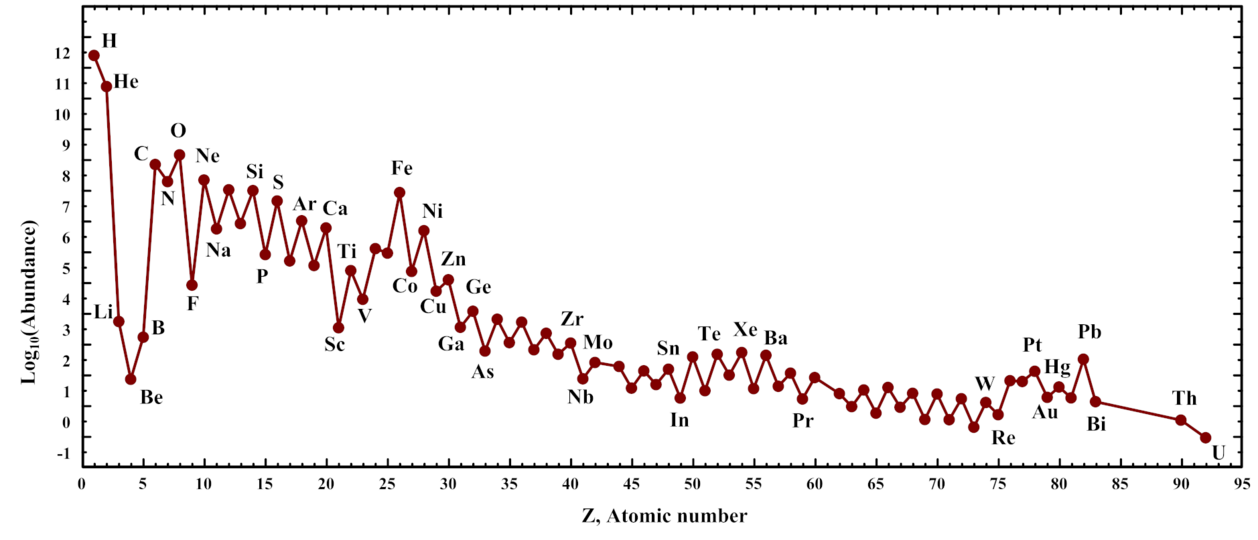
Figure courtesy of
MHz`as and Wikipedia ,
based on data in
Lodders, K., ApJ 591, 1220 (2003)
Q: How many hydrogen atoms are there for every single carbon atom?
Q: Do you notice a pattern in these abundances? Can you explain it?
Q: Why is the value for hydrogen set to 12?
My answers.
It's hard to see molecular H2, so find an alternative
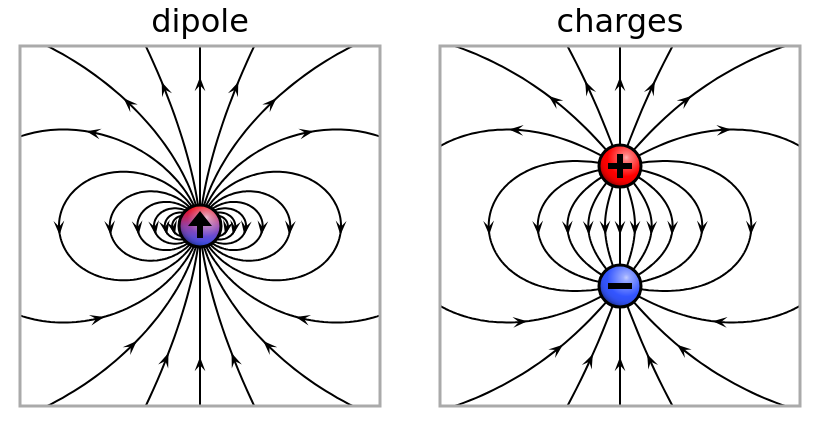
Diagram of electric dipole courtesy of
Geek3
and
Wikimedia.
Q: Can you think of any molecules which might meet these conditions?
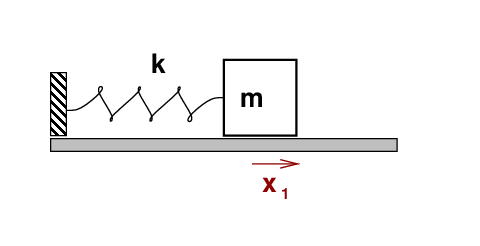
Q: What determines the frequency of this oscillation?
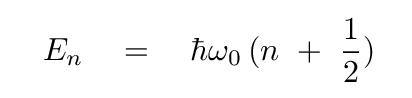
Q: What is the energy of a photon produced by this transition?
Q: What is the wavelength of the photon?
Q: In what region of the electromagnetic spectrum does this line appear?
My answers.
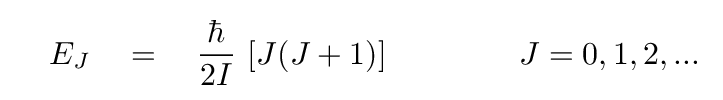
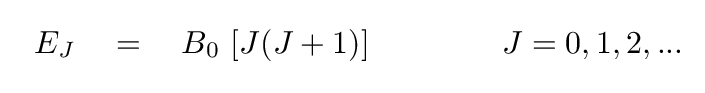
Q: Compare the constants in front of the expressions for energy
states in vibrational and rotational states for CO.
vibrational: E(n) = 0.269 eV * (n + 1/2)
rotational: E(J) = 0.00023825 eV * [ J(J+1) ]
Which type of transition requires the molecules to have
higher energies?
Q: Compute the energy of a photon emitted when a CO molecule
drops from J = 1 to J = 0.
Q: What is the wavelength of this photon?
My answers.
A group of astronomers measure CO emission from a cloud and
estimate the mass of the CO to be about 20 solar masses.
Q: What is the mass of the molecular hydrogen in the cloud?
My answer.
The role of dust in the creation of molecular hydrogen
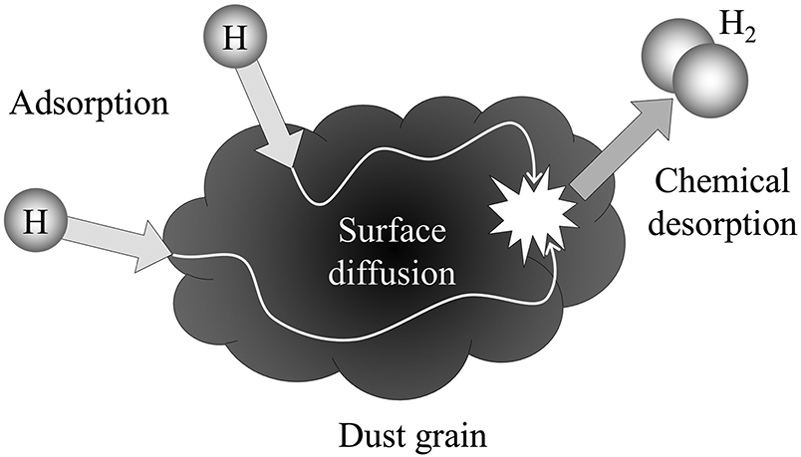
Figure 7.4 from
Ryden and Pogge, "Interstellar and Intergalactic Medium", Cambridge (2021) ,
after the original Fig 1 of
Delieu et al., Scientific Reports, 3, 1338 (2013)
Q: What is the typical speed of hydrogen atoms?
Q: What is the mean free path of a dust grain?
Q: How long between each collision of an H atom and the grain?
My answers.

Image of RCW 58 courtesy of
Mike Selby & Mark Hanson and Astronomy Picture of the Day
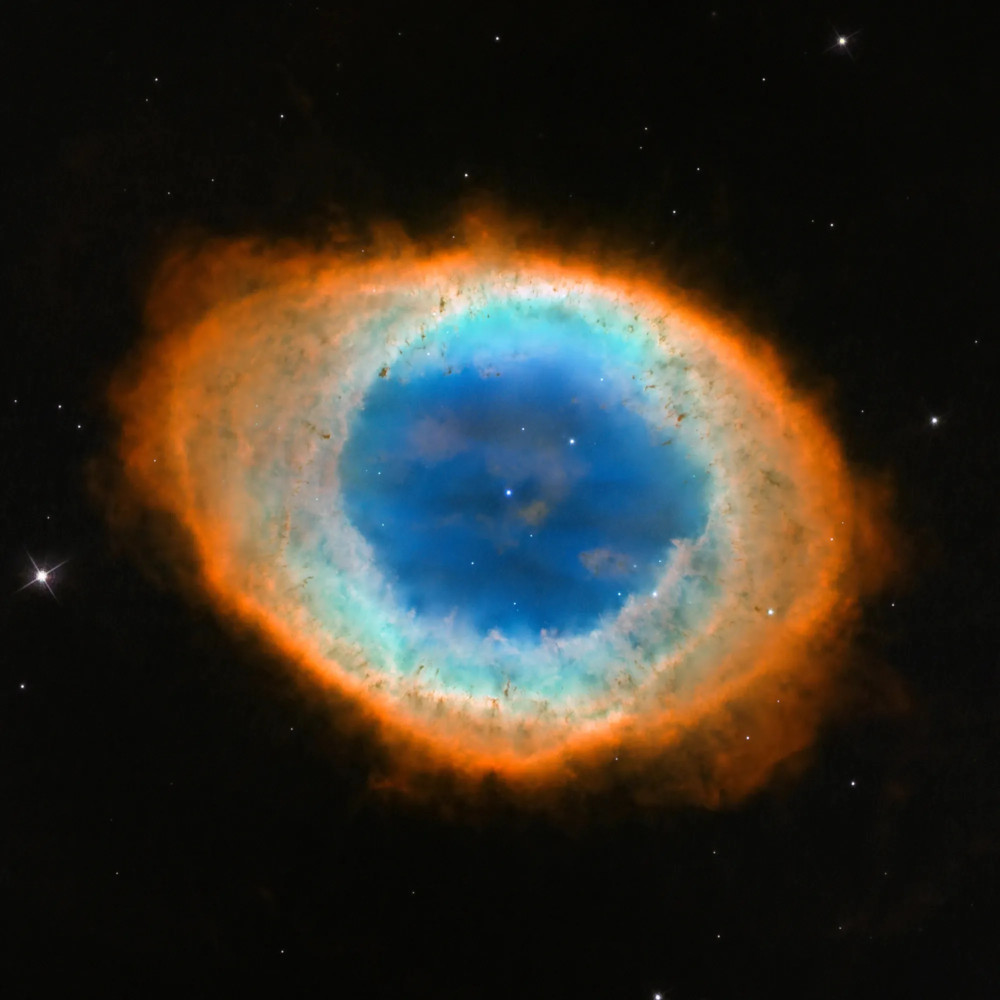
Image of M57 courtesy of
NASA, ESA and the Hubble Heritage (STScI/AURA)-ESA/Hubble Collaboration

Infrared image of M57 courtesy of
ESA/Webb, NASA, CSA, M. Barlow (UCL), N. Cox (ACRI-ST), R. Wesson (Cardiff University)

Chandra image of G292.0+1.8 courtesy of
NASA/CXC/UCSC/L. Lopez et al.
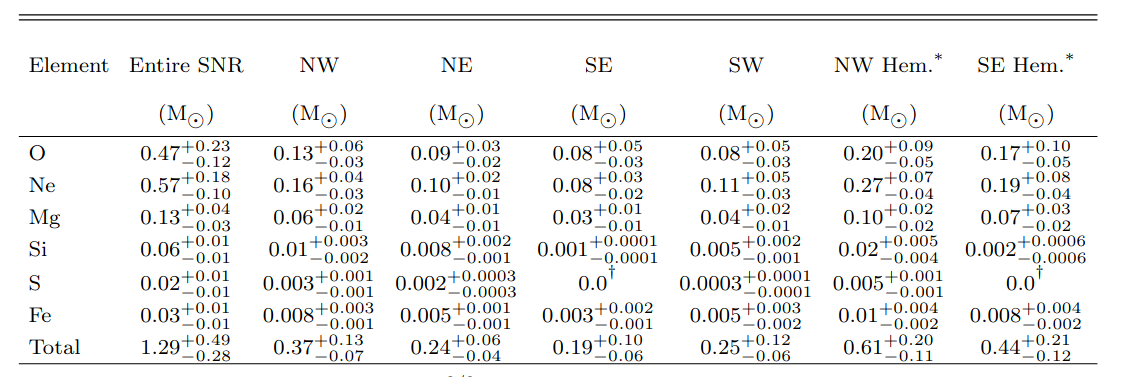
Table 4 from
Bhalerao, J., Park, S., and Schenck, A., ApJ 872, 31 (2019)
Destroying molecular hydrogen
Q: How hot must a star be in order to produce a large
fraction of its luminosity at these energies?
Q: Is the Sun hot enough?
My answers.
Dissociations regions at the edges of molecular clouds
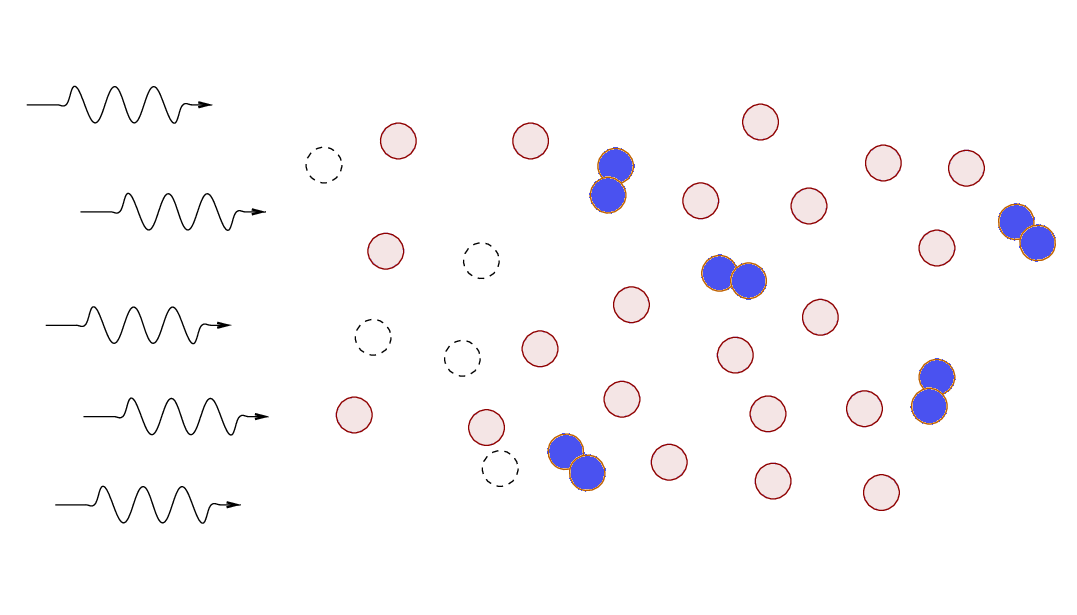
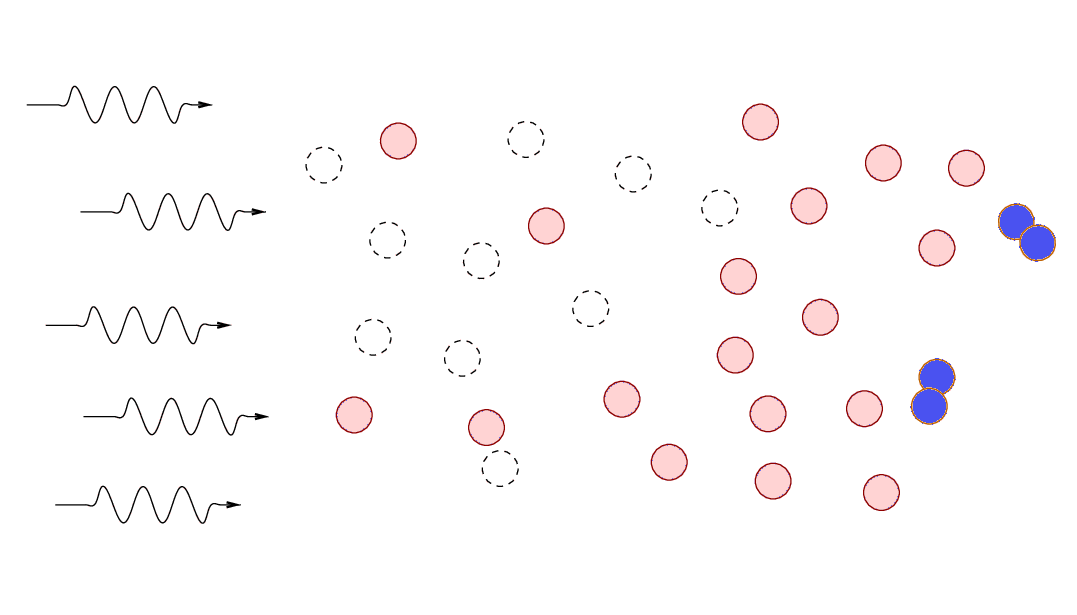

Image courtesy of
NASA, ESA, Hubble Space Telescope Orion Treasury Project Team, Massimo Robberto (STScI, ESA); Image Processing: Zoltan Levay (STScI), Joseph DePasquale (STScI)
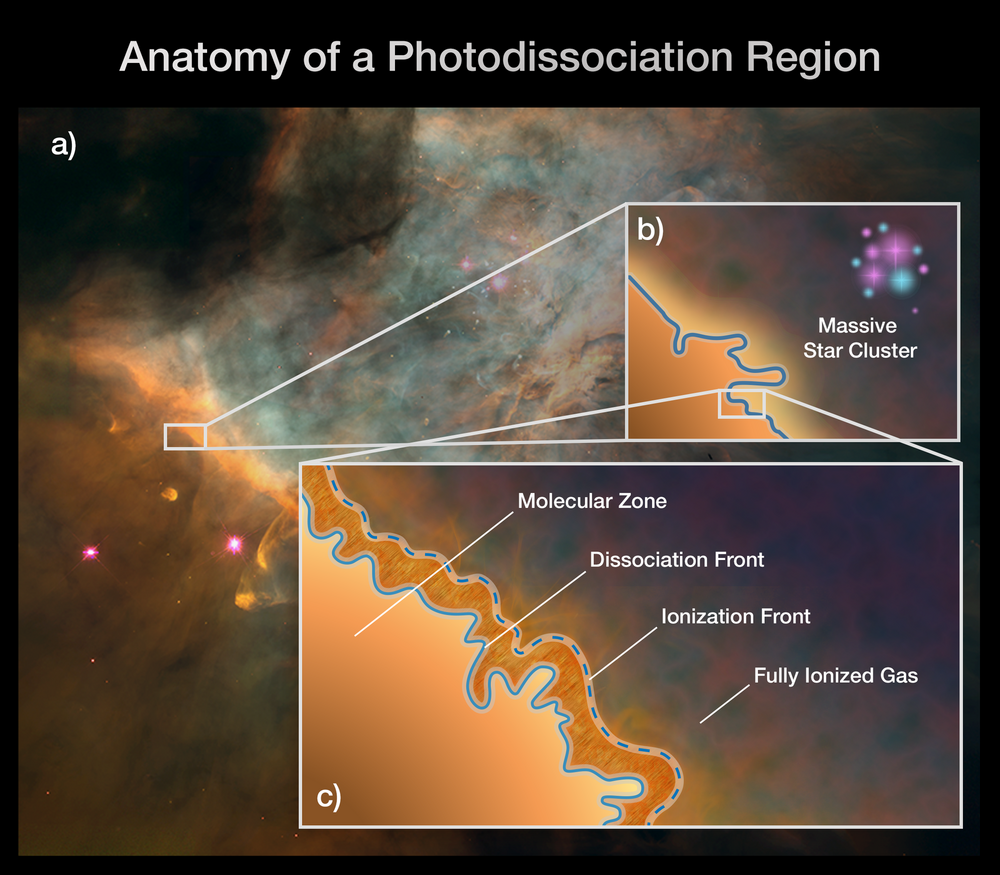
Image courtesy of
NASA, ESA, CSA, PDRs4ALL ERS Team, Jason Champion (CNRS), Pam Jeffries (STScI)
For more information
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.