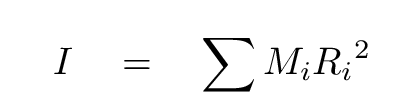
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Today, we will cover two topics.
Problems involving rotational motion often require one to know the moment of inertia of objects. Now, under certain simple circumstances, we know how to compute it:
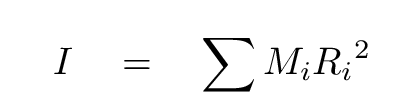
But what if the situation is not quite so simple? For example, suppose that the object IS a basic shape, but is NOT rotating around its center?
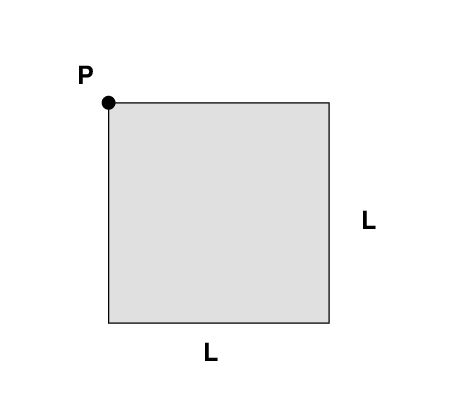
In this case, you can use the
Finally, what if the object in question is just not simple at all, but made of a material which changes in density from one location to another. In that case, we need to integrate around the rotation axis -- but take care to account for the mass of each section properly.
You've seen the rotational analog of simple 1-D kinematics, which answer questions like
But what about rotational dynamics, which addresses deeper questions, such as
Once again, we'll use your knowledge of physics in the linear world to guide us through the rotational realm.
A torque, it turns out, is a bit more complicated than a force; in order to compute the torque on an object, you need to know not only the size of the force involved, and the location at which it acts, but also the DIRECTION of the force.
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.