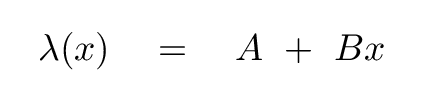
We now know how to compute the moment of inertia of a long, thin rod around one end, or around the middle. But we made one important assumption in those calculations: that the density was uniform, the same value everywhere in the rod.
But suppose that the density of the rod changes from one location to another? For example,
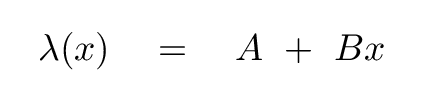
Q: What are the units of A? Q: What are the units of B?
In order to compute the moment of inertia of this variable-density rod around its left-hand end, we follow the same procedure we used for a constant-density rod. We break the rod up into teeny little pieces ...
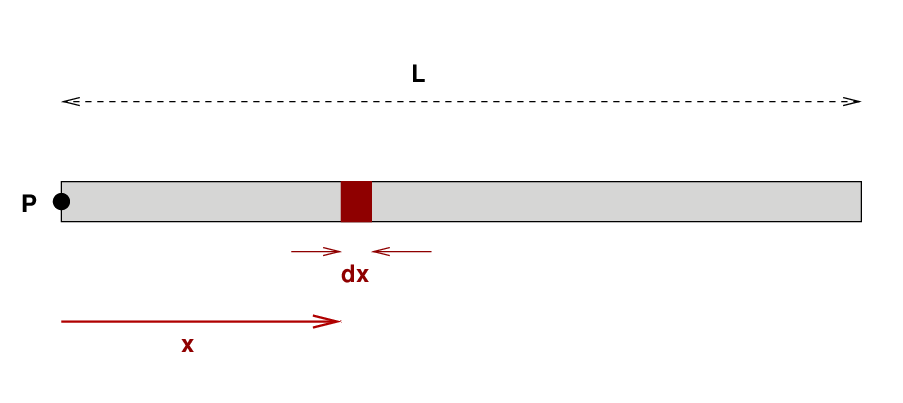
Q: What is the mass of the little section? Q: What is the moment of inertia of the little section around point P?
The little teeny mass dm of this small piece is
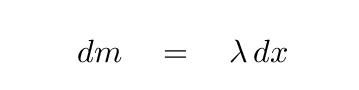
and so the little teeny moment of inertia dI is
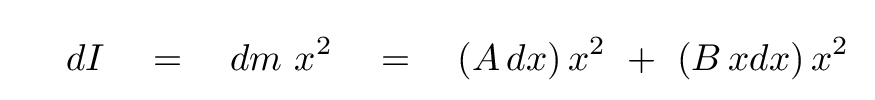
So, if we want the moment of inertia of the entire rod, we must add up the little teeny moments of inertia from all the little teeny pieces that make up the rod. In other words, we must integrate from one end of the rod to the other.
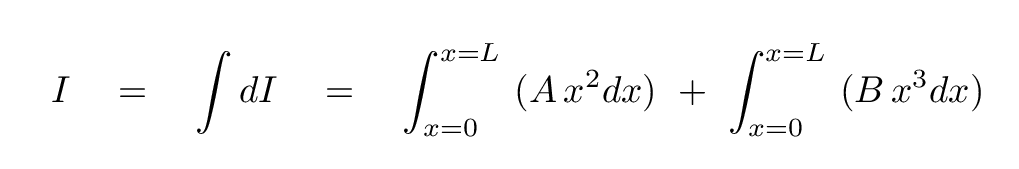
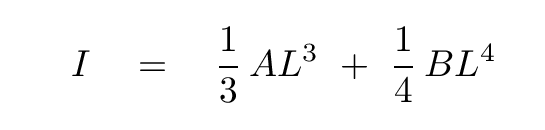
Let's check the units of the result: mass multiplied by distance-squared for the first expression, and mass multiplied by distance-squared for the second, as well. Good.
Let's try another example. Suppose that a long, thin rod of length L = 1 m has density
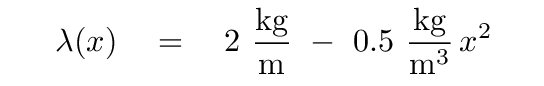
In order to compute the moment of inertia of this variable-density rod around its left-hand end, we follow the same procedure we used for a constant-density rod. We break the rod up into teeny little pieces ...

Q: What is the mass of the little section? Q: What is the moment of inertia of the little section around point P?
The little teeny mass dm of this small piece is
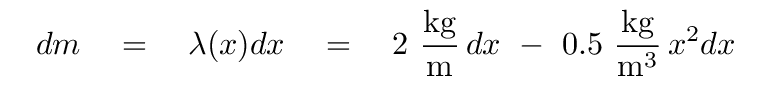
and so the little teeny moment of inertia dI is
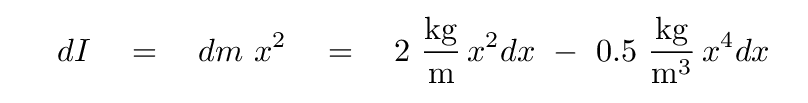
So, if we want the moment of inertia of the entire rod, we must add up the little teeny moments of inertia from all the little teeny pieces that make up the rod. In other words, we must integrate from one end of the rod to the other.
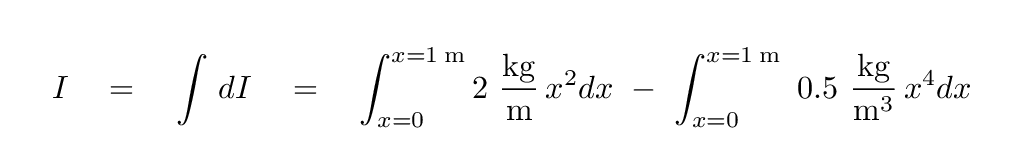
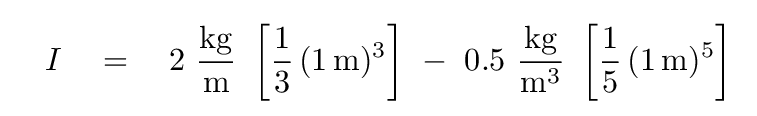
And the end result is that the moment of inertia of this variable-density rod is I = 0.57 kg*m2.
If you have some extra time, you might calculate the mass of this rod ....