Computing the moment of inertia of an extended object

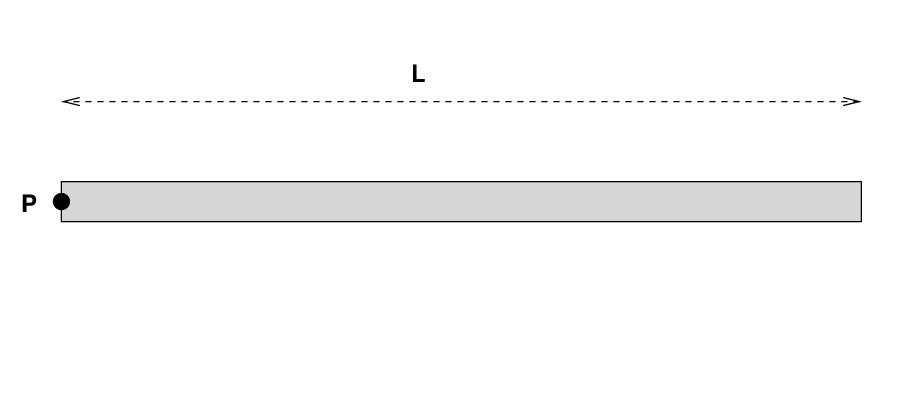
We know how to compute the moment of inertia of a collection of compact little masses. Fine. But there are plenty of objects which are more like extended, continuous distributions of matter; for example, a long, thin rod, of mass M and length L. Suppose that this rod can pivot around its left end.

How can we compute the moment of inertia of this rod around the pivot point P?

The first step is to determine the linear mass density -- that is, mass per unit length.



  Q:  What is the linear mass density λ of this rod?

Right.

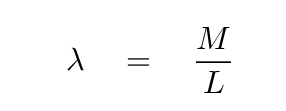
Good. Once we know the linear mass density, we can compute the mass of any little piece of the rod. Consider, for example, the little section marked below. We use the notation dx to stand for "a little teeny length."



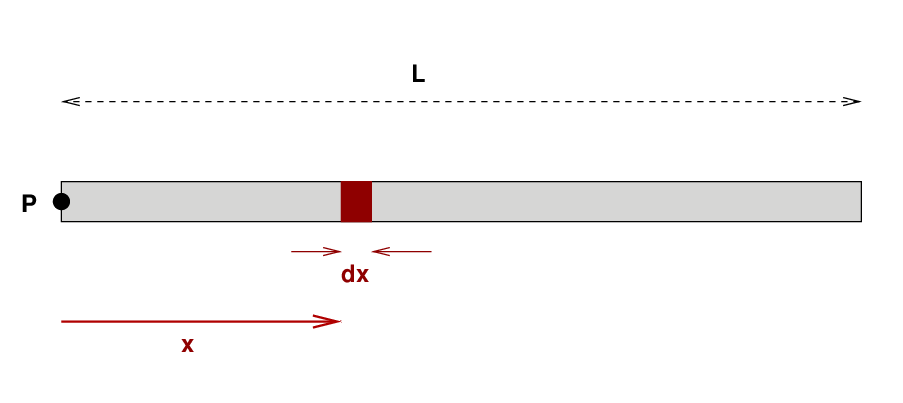
  Q:  What is the mass of the little section?


  Q:  What is the moment of inertia of the little section around point P?

The little teeny mass dm of this small piece is

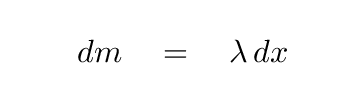
and so the little teeny moment of inertia dI is

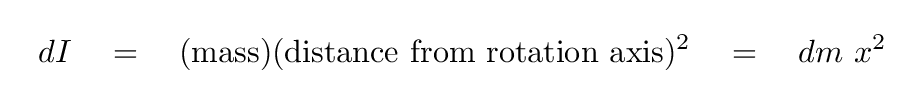
So, if we want the moment of inertia of the entire rod, we must add up the little teeny moments of inertia from all the little teeny pieces that make up the rod. In other words, we must integrate from one end of the rod to the other.

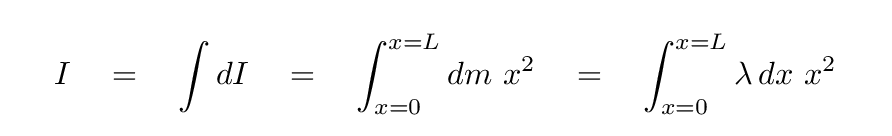
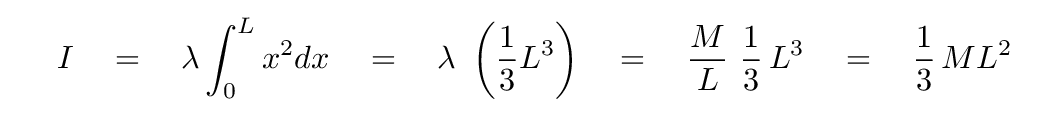
Let's check the units of the result: mass multiplied by distance-squared. Yes, that's moment of inertia, all right.

Let's try a variation. Suppose that the rod pivots around its CENTER, instead of the left-hand end. What is the moment of inertia around this central location?

(Hint: set up a coordinate system with the center of the rod at x=0)


  
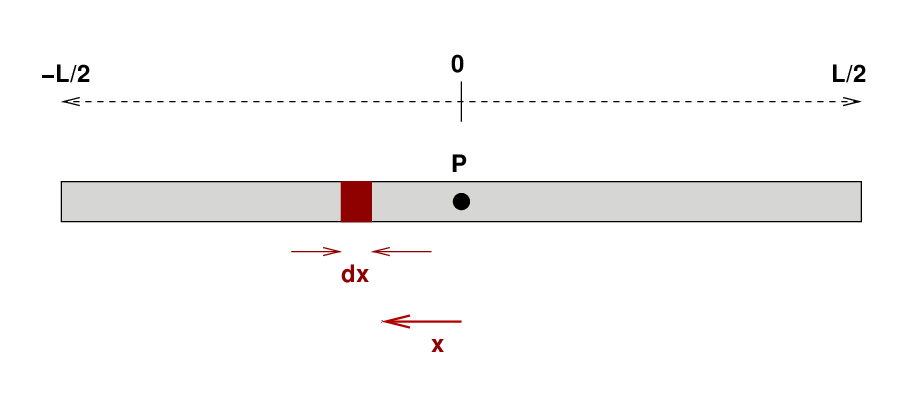
  Q:   What is the moment of inertia of the rod around its center?

The setup looks very similar to our previous integral. The only difference is in the limits.



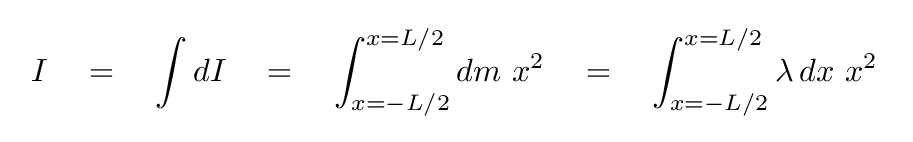
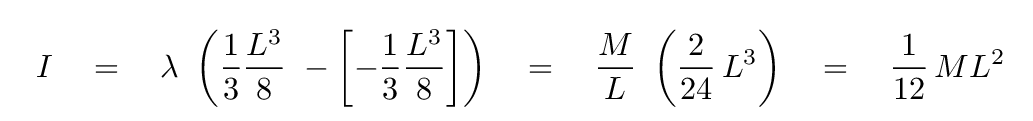
  Q:  Based on these moments of inertia, is it easier to rotate
           a rod around one end, or around the center?

 
  Q:  Does that make sense?