Practice problems for Test 2

  1. Consider the system of three identical springs, of spring constant k = 24 N, shown below. There are two blocks, one of mass m = 2 kg and the other of mass 4m = 8 kg.

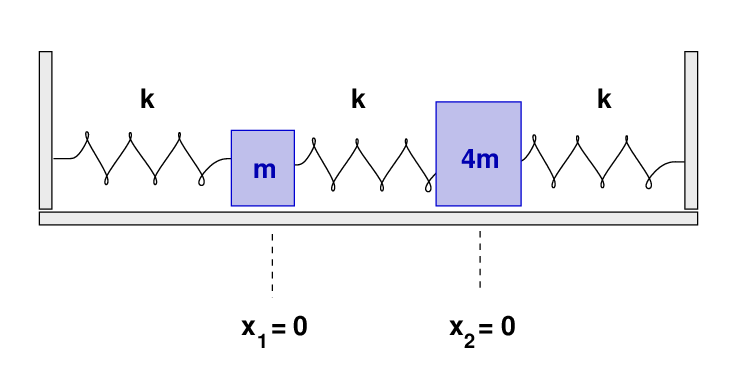
    1. What are the frequencies of the normal modes of this system? Call the lower frequency ω1 and the higher frequency ω2.
    2. What are the eigenvectors corresponding to each frequency?

      3. There will be two normal modes of oscillation, which can be described as

      Suppose that, at time t = 0, the blocks are set so that x1 = 2 m , x2 = 0 m , v1 = 0 m/s , v2 = 0 m/s .

    3. What are the values of the coefficients A1, A2, φ1, φ2, in the equations for the normal modes?
    4. Write an equation giving the position of block 1 (the 2 kg mass) as a function of time.

    Answers to problem 1:

  2. An ordinary molecule of carbon monoxide is made up of ordinary carbon and oxygen atoms: 

    
             mass of ordinary carbon   mC = 12 mH
             mass of ordinary oxygen   mO = 16 mH
    where 
    
             mass of ordinary hydrogen mH = 1.67 x 10-27 kg

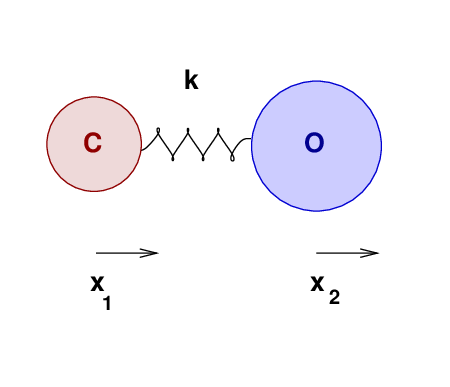
    The force constant of the bond between these atoms is k = 1860 N/m. Suppose that these two atoms vibrate in their first normal mode.

    1. What is the angular frequency ω of this oscillation?
    2. If a vibrating molecule emits all its energy as an infrared photon, what will the wavelength of that photon be?

      3. A very small fraction, about 0.2 percent, of all oxygen atoms have two extra neutrons in their nucleus. These "heavy" oxygen atoms, called 18O atoms, have a mass which is 18 times mH. Suppose that one such "heavy" oxygen atom joins with an ordinary carbon atom to create a "heavy" carbon monoxide molecule, and suppose further than the force constant of the bond remains unchanged.

    3. What is the angular frequency ω of a "heavy" CO molecule in its first normal mode?
    4. If a vibrating "heavy" CO molecule emits all its energy as an infrared photon, what will the wavelength of that photon be?

      5. Answers to problem 2: