One more boundary condition: radiative end

We've used two boundary conditions so far:

Now, let's look at the last boundary condition you'll need for the final goal of computing the technique which will create the perfect hamburger: a radiative end to a section.

If one section of an object is exposed to the outside environment, then it can radiate away heat to the environment -- or absorb heat from the environment. We'll adopt the simple assumption that the object radiates and emits like a blackbody.

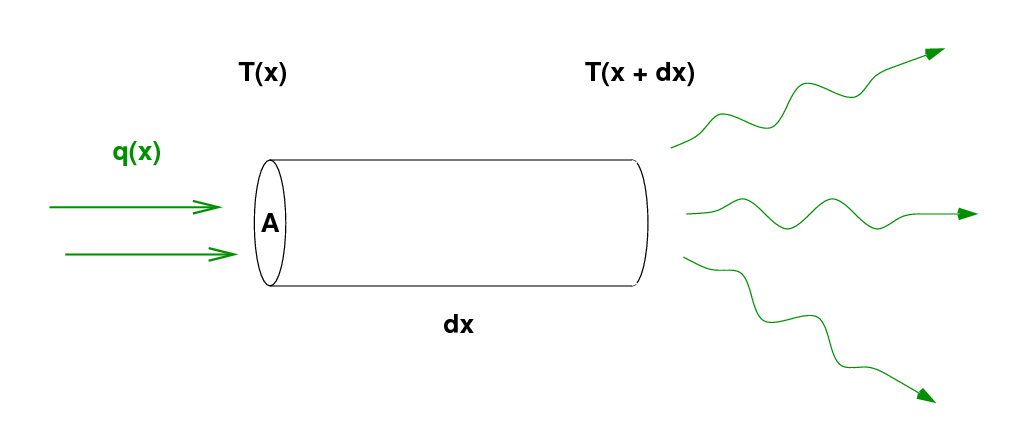
Let's look again at one small section of a metal rod. The section has a width dx and a cross-section area A. We are interested in the amount of heat flowing through this little section of the rod. We'll use the convention that rate at which energy flows through the section, q(x), is positive if the energy flows in the positive X direction. The units of q are 


                                Joules
     q   =   heat flow   =   -----------
                               s * m^2

The energy radiated away from this little section depends on the temperature of the section and the area of the end.

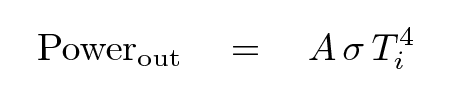
where 



    A             is area of the end of the segment
                           (m^2)

    σ             is the Stefan-Boltzmann constant
                           (J / s*m^2*degK^4)

    T             is the temperature of the material
                           (degK)

Of course, radiation from the outside world can also be absorbed by this exposed tip.

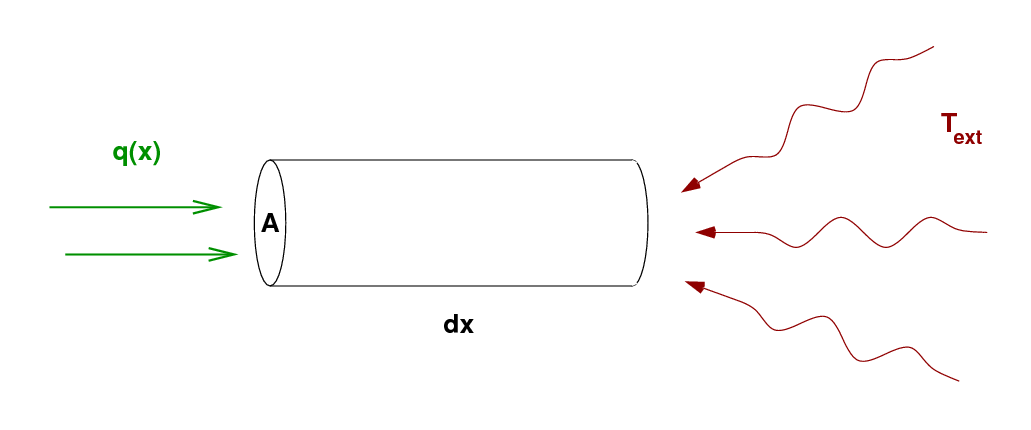
The amount of energy it absorbs is

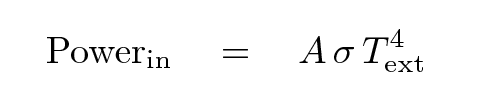
where 



    A             is area of the end of the segment
                           (m^2)

    σ             is the Stefan-Boltzmann constant
                           (J / s*m^2*degK^4)

    T             is the temperature of the outside world
     ext                   (degK)

Putting it all together inside ground beef

Eventually, you will face a challenge: compute the temperature throughout a hamburger patty as it sits on a hot grill. This is a three-dimensional situation, so it's a bit more complicated than any of the models you have run so far. You can still apply the same rules, though.

It may make sense to break up your calculations into several groups, depending on the situation of each piece of meat.

If a piece does NOT lie at a boundary ...
... then the change in temperature depends on the sum of the second derivatives in all directions:

If a piece has one boundary with fixed temperature only ...
... then the change in temperature STILL depends on the sum of the second derivatives in all directions; after all, you know the temperature in all directions, right?

If a piece has at least one boundary exposed to the outside ...
... then you are stuck with a long calculation. You need to compute the flow of heat in or out through all faces of the piece (there will be 6 faces for a 3-D cube), then use the specific heat of the material to compute the change in its temperature.

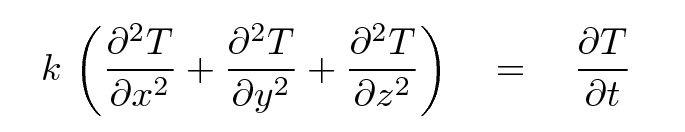
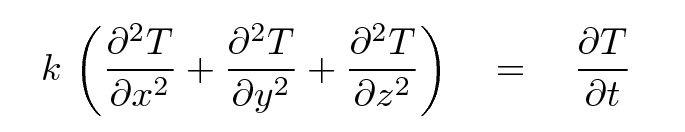
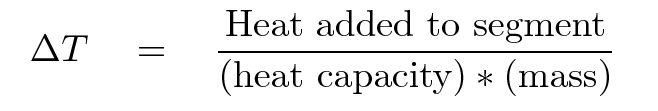
When you move to 3-D calculations, you will find that the conditions for numerical stability become more severe: you may have to use very small timesteps and/or space-steps to prevent instabilities from ruining your results.

Now, in order to make a hamburger which a person would really want to eat, it is necessary to flip it over at least once (and perhaps several times) on the grill; otherwise, one side burns while the other one remains nearly frozen. 



  Q:  How can you incorporate a "flip" into
      your simulation?