Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
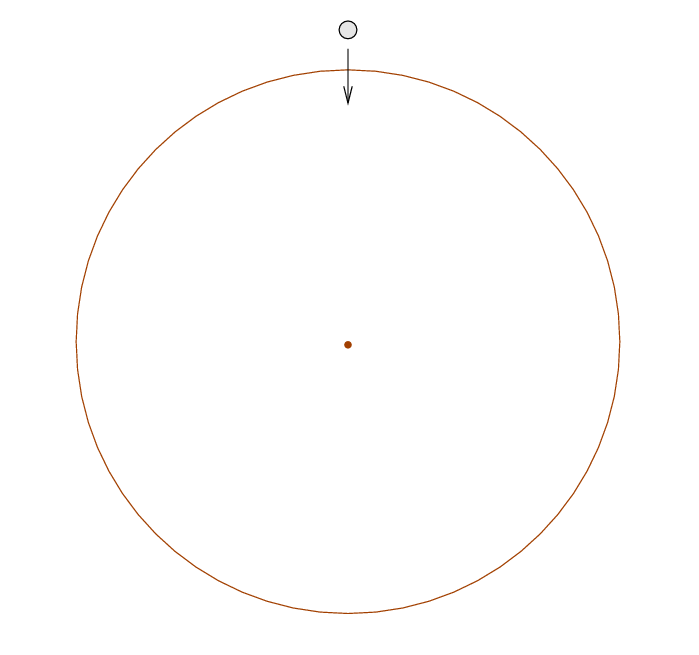
In the tiny_earth assignment , you had to simulate the motion of a ball which fell from about 6 million meters straight down toward a very compact object with the mass of the Earth.
Now, gravity is a conservative force, so it's clear what OUGHT to happen in this situation: the ball ought to fall inward, picking up speed, zoom past the central object, then gradually slow as it reaches the opposite side of the Earth. Eventually, it will fall back toward the center, and oscillate back and forth.
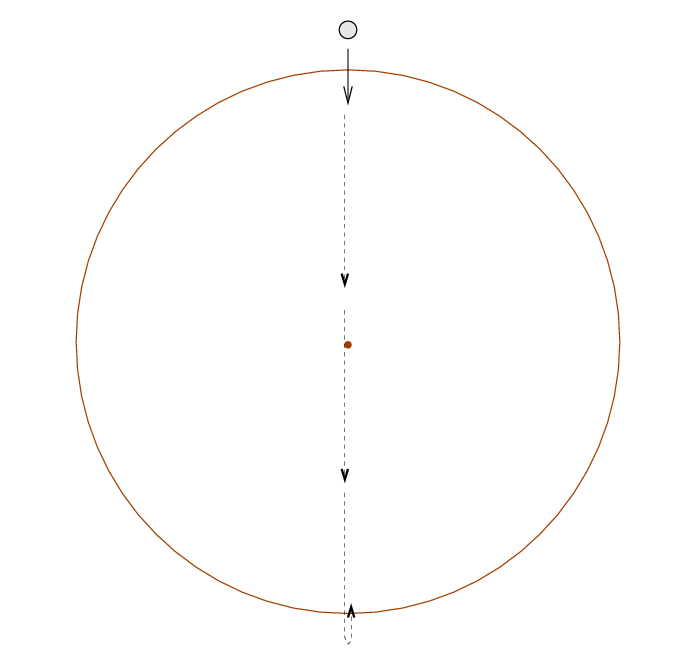
Here, for example, is the result from one of my simulations:
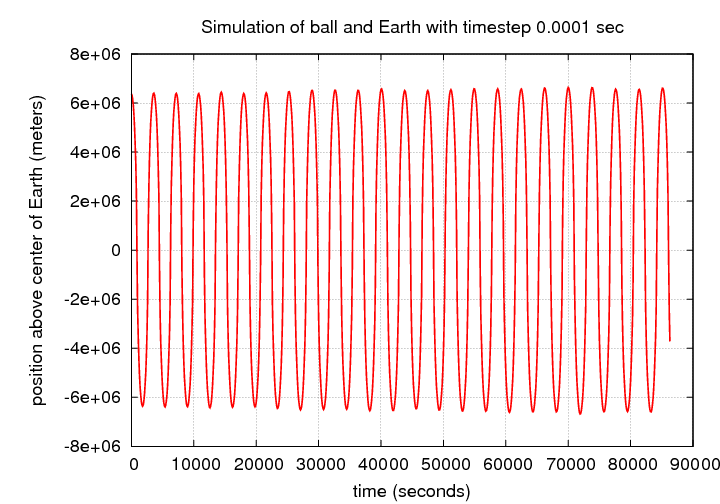
But in your simulations, I suspect that you found behavior of quite a different sort.
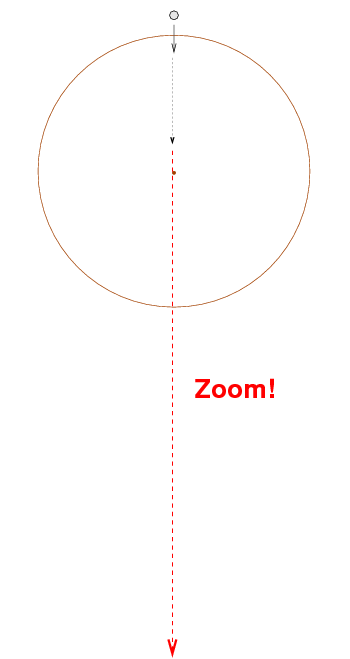
What causes the ball to fly away with a huge velocity, never to return? The problem is the nature of the gravitational force: it has a magnitude which goes like 1 / r2. When the distance r between two objects becomes small, the force becomes very large -- and it changes very rapidly.
Let's look at the process of simulating the motion of a ball under this force, as the ball approaches the central source. The parameters are:
(You can find the MATLAB code in the "examples" section on the course web page )
When the ball comes very close to the massive central object, the acceleration grows to a very large magnitude. In one step, the ball acquires an enormous velocity and that velocity takes it PAST the central object, far beyond it to the far side. At the next timestep, the acceleration at that new location will be far too small to slow the ball down again. The result: the ball flies off with a huge -- and incorrect -- velocity.
This is a common issue in simulations, since inverse-square-law forces are pretty common. People have come up with several techniques for dealing with it.
The problem is the tendency for the force between two objects (and so the acceleration of each) to grow without bound when they make a close approach. We can prevent this from happening by modifying the Law of Universal Gravitation:
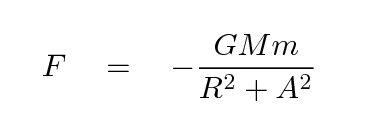
The quantity A above is the "softening parameter", so-called because it "softens" the very harsh force when the distance R becomes small. In essence, this technique places an upper limit on the maximum size of the gravitational force between two bodies.
The graph you saw earlier
was created using a softening parameter of A = 100 km .
Is this technically correct? Well, no. But it does (help to) prevent numerical integrations from going crazy if two bodies happen to come very close to each other. The motion of each object during their close approach will NOT be correct; but, after the objects separate again, and gain distances which are large compared to A, the motion once again will be computed (nearly) correctly.
If you don't really care what's happening during the close approach, this might be just fine.
If you just THINK about the motion of the ball and the compact massive object, you can figure out what _ought_ to happen. Use the conservation of energy: at the start of the simulation, the ball has some total energy
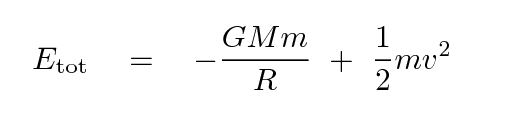
where R is the radius of the Earth, and v is the initial speed of the ball. As the ball moves, it ought to maintain its total energy, exchanging potential energy for kinetic as it falls, then going back to potential energy as it rises on the other side.
The motion ought to be symmetric, too. If the ball has velocity -v1 when it is at position R1 above the central object, it ought to have velocity -v1 when it is at position -R1 below the center, too.
We can use this fact, if we wish, to avoid all the unpleasant behavior associated with small radii. If we see the distance of the ball from the center decrease below some specific threshold, we simply "teleport" it to the other side of the center and give it exactly the same velocity.
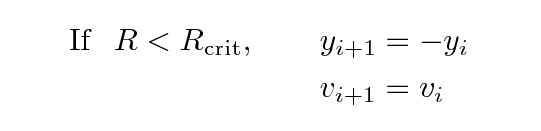
In this way, we magically items so that they jump from an approaching situation to EXACTLY the corresponding receding situation. We ignore all the possible non-gravitational interactions which might occur during that close approach.
The notion of "teleportation" is sort of wacky, I admit. But it carries the flavor of this idea. If one wants to be more rigorous, one can leave the numerical integration when two bodies approach within a critical threshold, and, using their current positions and velocities, apply analytic formulae to compute their positions and velocities at future times during the close approach. The 2-body problem CAN be solved analytically, if you are willing to ignore all the objects which might also be exerting gravitational forces on the objects.
This general idea can be described as a hybrid approach: use one technique (numerical integration) when objects are far apart, but a different technique (analytic formulae) when two objects come very close to each other. There are many types of hybrid approach; one variant is named "treecode". I'll describe this in class.
One factor which contributes to this runaway behavior of objects during a close approach is the gigantic size of the distance an object can travel in a single timestep, under the influence of a large acceleration. If we could prevent each body from jumping so far from one step to the next, we might allow the forces on the object after its close approach to slow it down properly as it recedes.
So, if we realize that one pair of objects has reached a dangerously small separation, we might change the size of the timestep. This does NOT avoid the singularity at a distance of zero -- the force and acceleration will still become infinite -- but, if the two objects are merely passing each other, and not really colliding, using a small timestep can fix the problem.
Q: How could you determine that two objects have reached that threshold at which the timestep should be decreased?
Of course, after the two have moved far apart, it would be a good idea to increase the stepsize again.
But suppose that you have a set of 10 objects -- planets in a solar system, for example -- and only 2 of them are close enough to cause a problem. If you decrease the stepsize for ALL the objects, then you'll be doing a great many unnecessary calculations. Just because an asteroid is zipping past the Earth, requiring you to check its motion every 10 seconds, does NOT mean that you should also be computing all the forces acting on Neptune every 10 seconds.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
