The RIT Telescopes

• Designs for Optical Telescopes
• The Meade 12-inch LX-200 at RIT Obs
• Using the RIT 12-inch Telescope
• Using the RIT 14-inch Telescope

Designs for Optical Telescope

There are several common designs for optical telescopes.

• Refractors use a lens to focus incoming light.
  

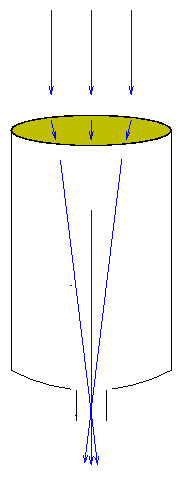
  Light passes through a lens at the front of the telescope tube and comes to a focus near the back of the tube. The design doesn't work well for large telescopes for two reasons:

  1. its is difficult to cast a large piece of glass without internal bubbles or flaws
  2. one can support the lens only around the edges; a large lens will sag under the force of gravity, distorting its shape and focus

• Newtonian reflectors use one parabolic mirror to focus incoming light, and a second flat mirror to send the light sideways to an eyepiece or camera.
  

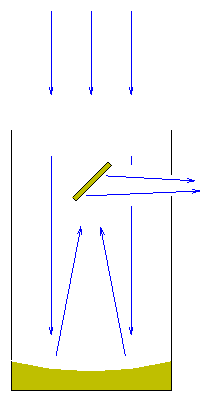
  Light never passes through a lens -- it only bounces off the surfaces of mirrors. This reduces the amount of light lost as it makes its way through the optical system. Moreover, the mirrors can be supported around their edges and along their back surfaces.

  On the other hand, the secondary mirror blocks some of the incoming light, and slightly blurs the light which does reach the focus.

• Schmidt-Cassegrain telescopes combine a weak lens at the front of the telescope with a pair of mirrors.
  

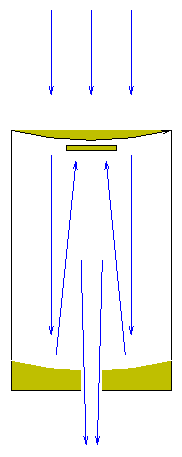
  Yes, yes, the photograph shows a Maksutov instead of a true Schmidt-Cassegrain. The two designs both fit the desciption given, which is almost always called "Schmidt-Cassegrain". If you knew that "catadioptric" would be a more technically correct term, good for you.

  This seems to combine the worst of both worlds: light must pass through a lens, and a secondary mirror blocks part of the aperture. However, since this combination of elements can yield a relatively long focal length with a wide field of view in a compact package, it is often adopted for practical reasons.

The Meade 12-inch LX200 at RIT Obs

The Meade Instruments Corporation makes many different types of telescopes. The RIT Observatory owns a 12-inch Meade LX200.

The components of the system are

• pier to hold the telescope up off the ground
• equatorial fork mount
• electronic control system
• optical tube assembly (OTA)
• finder telescope
• eyepiece (or camera)

The OTA is a 12-inch f/10; that means the clear aperture is 12 inches in diameter, and the focal ratio

                       focal length
        focal ratio =  ------------   =  10
                         aperture 

Exercise: What is the focal length of the telescope?

We can attach a focal reducer to the back of the telescope, which reduces the focal ratio to f/6.3; it provides a wider field of view, which makes finding objects much easier.

Exercise: What is the focal length of the telescope with the f/6.3 focal reducer in place?

A brief digression on Plate Scale

The effective focal length of an optical system is a very important number: it determines the plate scale of any instrument attached to it. "Plate scale" is simply the physical distance on the focal plane between two objects which subtend a given angle (usually one arcsecond) on the sky.

Imagine that the telescope and all associated optics to be a black box which focuses light and forms an image:

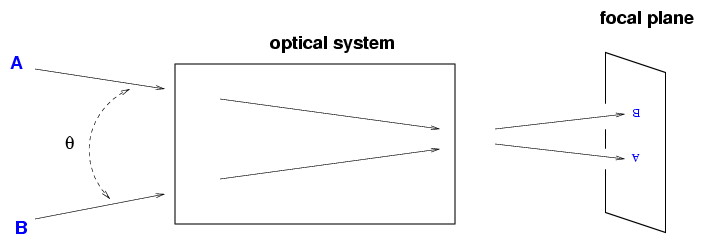
If we zoom in on the right-hand side of this diagram, we can draw this diagram:

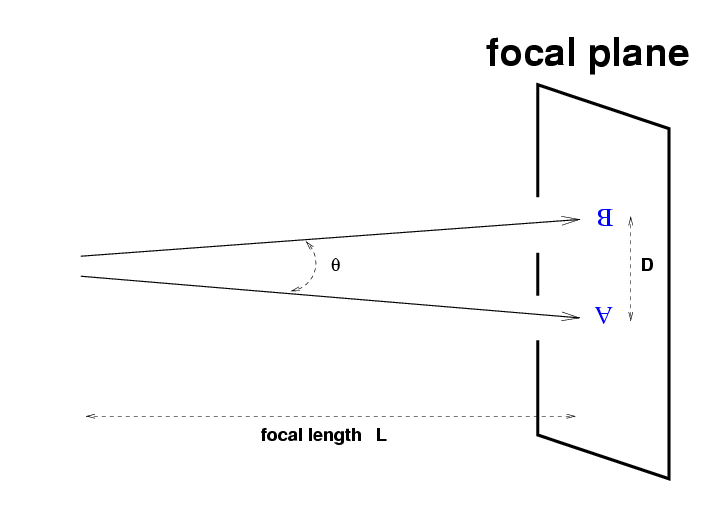
The physical distance D between two celestial objects separated by an angle theta is

             D  =  L * tan(theta)

             D  =  L * theta

Exercises:

1. What is the plate scale of the RIT 12-inch telescope without a focal reducer? Express your answer in units of arcseconds per millimeter.

2. One of our CCD cameras has square pixels which are 9 micrometers (9 microns) on a side.
   1. What is the smallest angle which can be resolved on pictures taken with this camera, using our 12-inch telescope at f/10?
   2. The planet Saturn is a nice target this spring. Right now, the rings are about 45 arcseconds in diameter. How many pixels will Saturn's ring span?

3. The CCD chip of this camera is 1536 rows high by 1024 columns wide.
   1. What is the field of view when it is mounted on our 12-inch telescope at f/10?
   2. Roughly what fraction of the full lunar disk will fit onto a single picture?

Using the RIT 12-inch Telescope

The telescope is mounted on an equatorial mount: moving a single gear causes the telescope to track the motion of celestial objects as the Earth rotates. Some telescopes are placed on alt-az mounts, which are simpler to build, but less convenient to use: one must slew around two axes to follow objects in the sky, and the field of view will slowly rotate with respect to the stars.

I have aligned the RIT telescope's mount so that it can track objects for long periods without losing them from the field of view. However, the gears which drive the RA motion have an unfortunate amount of slop; the telescope's precise position oscillates a little bit over a period of several minutes. The wobbles are large enough to give stars short trails in any exposure longer than about 20 seconds.

One can control the telescope manually, using a "hand paddle" with keys to slew it North, South, East or West. One can also connect the telescope to a computer running any one of several planetarium programs, and use the program to move the telescope. A computer in the dome has one such program installed.

In order to use the telescope, one should follow these steps:

1. open the telescope dome slit; wait for the slit to open fully, and give dust a bit of time to settle to the floor
2. remove the plastic bag which covers the telescope
3. remove the big lens cap from the front of the telescope
4. place lens cap on short white file cabinet, with plastic bag sitting in it
5. turn on telescope power: first flip a switch on a unit on the floor at the base of the pier, then flip a second switch on the telescope fork
6. after telescope's system finishes booting, it will ask you about Daylight Savings, the current date, and the current time; answer the questions using the keys on the paddle. The paddle display should now read Align -> One star
7. walk outside the dome, find a bright star in the sky (Altair is a reasonable choice in the fall, Regulus in the spring)
8. using the arrow keys on the handpaddle, slew the telescope manually so that it points at the star
9. make sure that the star is centered in the main telescope and in the little finder scope; you may need to adjust the finder's mounting screws
10. press "Mode" on the paddle to back up to the main menu
11. choose "Object" -> "Star" -> "Named" on the handpaddle, then scroll through the list of names to choose your star
12. press "Enter" on the handpaddle. The display will give the name of the star.
13. press again and hold the Enter key for about 2 seconds. When you release the key, the display should say, Press enter to synchronize.
14. press the Enter key. This tells the telescope that it is right now pointing at that star you selected.

At this point, one should be able to give the coordinates (or catalog number) of a desired target, command the telescope to slew, and expect to find the target in the field of view.

One can focus the telescope by rotating the LOWER of the two silver cylindrical knobs on the back of the tube:

The shorter, upper knob locks the mirror in place for shipping.

Turning this lower knob moves the primary mirror forward and backward in its cell, which is a stupid way to focus, for two reasons: first, the separation between the primary and secondary mirrors should be fixed at an optimum distance to yield the best images. Second, moving the primary mirror can tilt it slightly, which can cause objects to move sideways in the field of view, sometimes even leaving the field. If one switchs from the CCD camera to the eyepiece, one must turn the knob between 2 and 3 full rotations. When one is trying to focus precisely on the CCD camera, one should rotate the knob by just 5 so degrees at a time. It's annoying when focusing that one can't return exactly to a particular position -- one must simply turn the knob by an estimated amount.

To avoid these problems, we use an electric focuser on the back of the 12-inch telescope.

• moves the eyepiece/camera instead of the primary mirror
• avoids image shift during focusing
• provides finer control

The telescope's handpaddle can control the focus position: pressing the "Up" = "North" arrow moves the focuser one way, and the "Down" = "South" arrow the other way.

At the end of the night, one should shut the telescope down in the following order.

1. slew the telescope so that it points due south, roughly 45 degrees above the horizon
2. turn off the power

   Remove the CCD camera, if mounted

3. place the lens cap over the front of the tube and the small lens cap over the guider
4. place the big plastic bag over the telescope
5. close the dome slit

Using the RIT 14-inch Telescope

The 14-inch telescope is made by Celestron and has a focal ratio of f/10.

It sits on a German equatorial mount made by the Astro-Physics Corporation.

Watch out for the counterweights on the long bar as the telescope slews!

Exercise: How does the focal length of this telescope compare to the focal length of the 12-inch telescope (without any focal reducers)?

One can control the telescope via a handpaddle, though the look and feel of this one are quite different than the handpaddle on the 12-inch. In theory, one can also connect a computer to the mount and use a planetarium program like Sky Map Pro to drive it around the sky.

In order to use the 14-inch telescope, one should follow these steps:

1. go into the rolloff structure and release the 3 red hooks which hold the roof in place. You must first move the latch handle to loosen the hook, then remove the hook from its ring on the roof. Hang each hook on the nail sticking out of the joist nearby.
2. if a short wooden plank is resting on the track on the left-hand (eastern) side of the building, remove it and place it on the table nearby. This piece of wood prevents animals from crawling into the building along the track.
3. walk outside to the southwestern corner of the building. Gently but firmly turn the far crank to slide the roof along its tracks. Continue until the length of cable between roof and crank is about four or five feet
4. remove the plastic bag which covers the telescope structure
5. remove the lens caps from each of the two finders attached to the telescope. Place the plastic bag and lens caps onto the table next to the computer monitor.
6. turn on telescope power: a 12-volt power supply resting on the pier
7. after telescope's system finishes booting, press "1" for the location, and "3" to Resume from park . In this control system, the Menu key acts to jump back up through the menu system to its base.
8. point the telescope at a bright star (Altair is a nice choice in the autumn, Regulus in the spring) using the N/S/E/W arrow keys on the handpaddle. You can use the "5" key to choose the speed with which the telescope will slew; slowest is 0.1 units, fastest is 1200 units. You'll want to pick 1200 for this job.
   • first, slew the telescope so that the bright star appears in one of the finders
   • next, put an eyepiece into the main telescope and center the star in the eyepiece
9. choose "Objects" -> "Tour" -> "Constellation/Star" on the handpaddle
10. scroll through constellations to reach the one containing your star (Aquila = Aql, if you are pointing at Altair)
11. choose the Greek letter designating your star (alf = alpha, if you are pointing at Altair)
12. select the "Sync on star" option via the ">" key on the paddle; confirm by pressing "1" to synchronize the telescope on your star

And now you should be able to select a star or galaxy in the paddle's database and slew directly to it.

One tricky thing about German equatorial mounts is that they divide the sky into two halves: east of the meridian, and west of the meridian. As a mount is tracking an object, if the object drifts from the eastern to western side of the meridian, the telescope will suddenly make a big slew to rotate around from one side of the pier to the other. This will also happen whenever you choose a new target on the other side of the sky. Note that the "North" and "South" buttons on the handpaddle will switch roles when you go from one side of the sky to the other, too; and, if you are taking pictures with a camera, the orientation of the pictures on the computer monitor will also rotate by 180 degrees. This can be very confusing late at night!

Exercises:

1. Once again consider our CCD camera which has square pixels which are 9 micrometers (9 microns) on a side.
   1. What is the smallest angle which can be resolved on pictures taken with this camera, using our 14-inch telescope at f/10?
   2. The planet Saturn is a nice target this spring. Right now, the rings are about 45 arcseconds in diameter. How many pixels will Saturn's ring span?

2. The CCD chip of this camera is 1536 rows high by 1024 columns wide. What is the field of view of the camera when mounted on the 14-inch?
3. What is the ratio of area covered by the camera on the 14-inch to area covered by the camera on the 12-inch?
4. Which telescope do you think is easier to point to some obscure, faint little target?

Copyright © Michael Richmond. This work is licensed under a Creative Commons License.