 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
There are a number of phenomena in astronomy which give rise to periodic signals:
If you suspect that your target is varying in a regular way, how can you find its period? Today, I'll give some general background on the analysis of a periodic signal, and then explain in detail one of the many different methods for finding the period: the string-length technique.
Consider a very simple periodic signal:

A sine wave described by
y = 3 * sin( x )
We can describe this signal with two parameters:
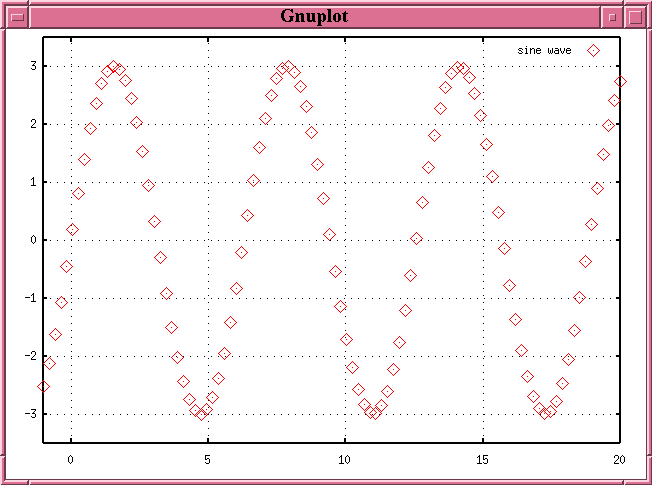
If we have a very long stretch of data, and we plot the signal versus time, we end up with a very long graph:
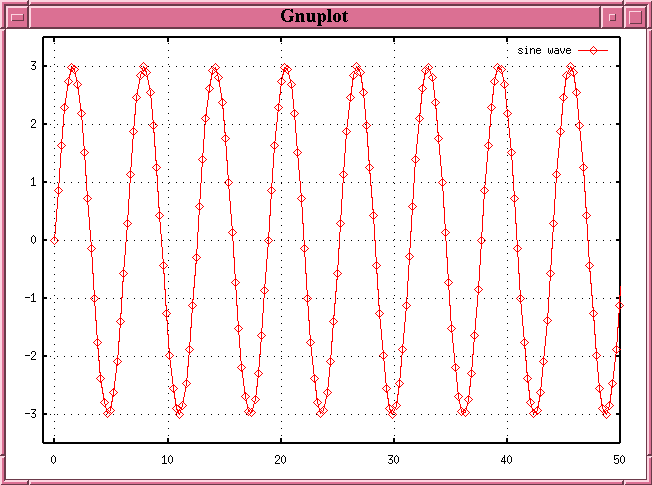
It is possible to squish a very long stretch of data onto a small graph if one converts the time variable to a related quantity: phase. Phase is defined as the fractional portion of the number of periods which have elapsed at a given time:
t
phase at time t = fractional portion of ( --------- )
period
t t
= -------- - int ( ---------- )
period period
The phase ranges over a fixed, small range: from 0.0 (start of a period) to 1.0 (end of a period). If we take that same sine curve as before, with data running from time t=0 to t=50, and this time plot its value versus phase, we get a very simple graph:
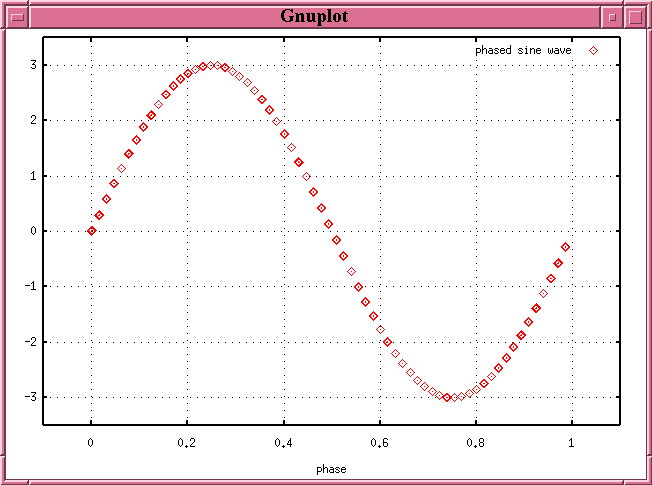
This has nice features:
As you will see below, we can use phase diagrams to figure out the period of an unknown signal.
What happens if we try to calculate the phase of a signal, but do so with the wrong period? Once again, we'll use a simple sine curve to illustrate. But this time, we'll calculate the phase with a period slightly different from the true value. When we plot the points in a phase diagram, we see this:
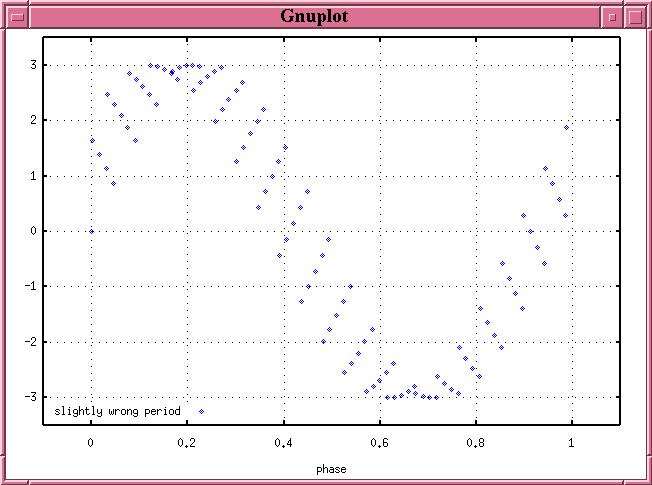
Hey! The phased data no longer lie along a single, smooth locus in the diagram. Instead, they form a wide band. This is a signal that the period used to calculate the phase was incorrect.
If we use a period which is far from the true value, the phased data scatter all over the diagram:
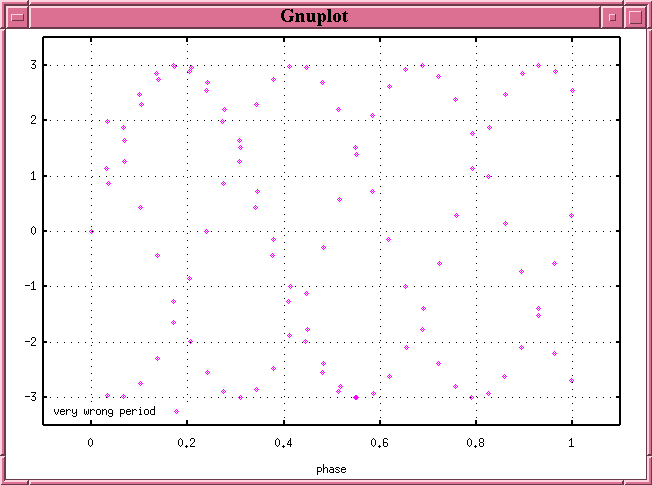
Only if the proper period is used to calculate the phase will the data fall along a single, narrow path in the phase diagram. We can use this fact to determine the period: pick a period, calculate the phase, and plot the resulting phase diagram. Modify the period and repeat until the points fall along a narrow locus.
The method ought to work, but it sounds pretty subjective; is there any way to make it quantitative? Yes! The string-length method provides a numeric metric for assessing the "narrowness" of the locus of points in a phase diagram. A good reference is the paper A period-finding method for sparse randomly spaced observations of 'How long is a piece of string?' by Mike Dworetsky, MNRAS, 203, 917 (1983); you can find it on-line at
http://adsabs.harvard.edu/cgi-bin/nph-bib_query?
bibcode=1983MNRAS.203..917D&db_key=AST&high=3c321cbf8321100
The idea is simple:
LOOP:
The period which yields the smallest sum of lengths ("shortest piece of string") is the best estimate of the true period.
Give it a try! Here are some measurements of a variable star on several nights during the course of week:
Time (truncated Julian Date) Magnitude
---------------------------- -----------
12.46 8.417
12.55 8.500
12.64 8.835
12.73 9.167
12.79 9.261
13.45 9.267
13.54 9.078
13.63 8.707
13.69 8.499
15.52 8.836
15.61 8.503
15.70 8.415
15.79 8.632
17.68 8.530
17.77 8.880
A light curve of the star looks like this:
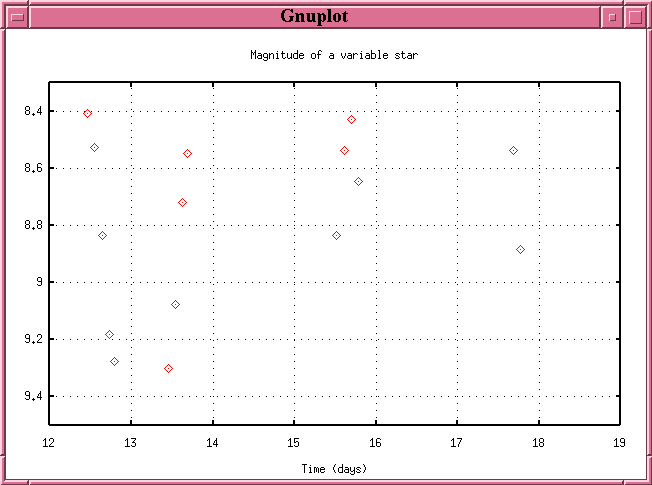
Make a guess at a reasonable range for the period -- it's some fraction of a day. Then, divide the interval into a number of pieces, and for each candidate period, make a phase diagram and calculate the string length. It takes time ... but one can easily program a computer to perform the calculations.
Jeff Robertson of Indiana University gave a very nice list of references for period-finding techniques in an E-mail to VSNET (vsnet-chat 131), which I reproduce below:
-----------------
An old but nice introduction and review to the four or five most popular period
finding methods can be found in [1] by Fullerton. This includes the various
"string-length" methods made popular by Lafler and Kinman [2]. This method has
been expanded upon by Stellingwerf [3] with the PDM method which is now a part
of IRAF. Most of the people I am associated with use FFT methods as prescibed
by Horne and Baliunas [4] and can now be found in the Numerical Recipes [5]
book. There is also a DFT method [6] which I am not to familiar with.
I am also interested in anyone else's methods and ideas...
References:
1. The Study of Variable Stars Using Small Telescopes, Fullerton, A.W. 1986,
ed. J.R. Percy, Cambridge University Press, p 201-218.
2. An RR Lyrae Survey With The Lick 20-inch Astrograph II. The Calculation
An RR Lyrae Survey With The Lick 20-inch Astrograph II. The Calculation
of RR Lyrae Periods By Electronic Computer, Lafler, J. and Kinman, T.D.
ApJS 11, p 216-222.
3. Period Determination Using Phase Dispersion Minimization (PDM),
Stellingwerf, R.F. 1978, ApJ 224, 953-960.
4. A Prescription for Period Analysis of Unevenly Sampled Time Series,
Horne, J. and Baliunas, S. 1986, ApJ 302, 757-763.
5. Search Algorithm For Weak Periodic Signals In Unevenly Spaced Time-Series,
Press, W.H. and Teukolsky, S.A., Numerical Recipes, Cambridge Univ. Press.
6. Time Series Analysis with Clean - Part One - Derivation of a Spectrum,
Roberts, D. H., Lehar, J., Dreher, J. W.,
1987, AJ, 93, 968.
which is illustrated in practice here ...
Discovery of a possible X-ray triple - 4U 1915-05,
Grindlay, J. E., Bailyn, C. D., Cohn, H., Lugger, P. M., Thorstensen, J. R.,
Wegner, G., 1988, ApJ, 34L, 25
-------------------
You can find a set of programs to do the job in various ways at the VSNET "Tools and Programs" site:
http://vsnet.kusastro.kyoto-u.ac.jp/vsnet/etc/prog.html
One of the best tools is the "AVE" program written by the Grup d'Estudis Astronomics in Spain.
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.