 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
When discussing the physics of Charge-Coupled Devices (CCDs), I described how photons knocked electrons free, and how one could move electrons via electrodes placed on the silicon surface. On the other hand, when discussing the properties of CCD images, I used the word "counts" to describe the value of each pixel. What's the relationship between electrons and pixel values?
The answer is ... it depends on the chip and the software used to read it out. The steps involved in reading the value of a pixel are something like this:
In both steps 3 and 4, one can scale the result by any arbitrary factor and the relative pixel values will remain the same. Some software allows the user to modify the scaling factor dynamically; others have a fixed setting.
The end result is that there is some "fudge factor" which relates the initial number of electrons in a pixel to the final number of counts reported by camera software. The ratio of these two numbers is the gain of the camera:
# of electrons per pixel
gain = --------------------------
# of counts per pixel
How should one choose the gain factor? There are several criteria.
It is logical to arrange the gain so that very roughly, the number of electrons in the full-well depth corresponds to the maximum pixel value.
The smallest difference one can represent in an integer image is 1 count. To some extent, it makes sense to arrange the gain so that 1 count corresponds to roughly the readout noise. Any finer measurement of the pixel values would yield differences which would be essentially random.
The SBIG CCD camera at the RIT Observatory has a gain factor which is pre-set and fixed. You can look in the FITS header for the GAIN keyword.
Exercise:
- What is the gain factor written into the header of our CCD images?
It is possible for you to check the value provided by a manufacturer. The basic idea is that if you look at a constant source of a LOT of photons (either a star, the twilight sky or a bright piece of cardboard), then the number of photons which strike the CCD in a series of exposures won't be exactly the same. Instead, the number of photons will have some scatter around an average value. The standard deviation of the number of photons should be
stdev (photons) = sqrt(number of photons)
So, if you were to take a series of pictures of a bright light source which averaged 16,000 electrons in each pixel, and calculate the mean and standard deviation of the number of ELECTRONS, you'd find
mean (electrons) = 16,000 per pixel
stdev (electrons) = 126 per pixel
However, when you measure pixel values from an image, you are actually measuring counts, not electrons. If the gain were exactly 1 electron per count then
mean (electrons) 16,000
mean (counts) = --------------- = ------------ = 16,000
electrons/count 1
stdev (electrons) 126
stdev (counts) = ----------------- = ------------ = 126
electrons/count 1
Note that
stdev (counts) = sqrt( mean counts )
But suppose that the gain was set to 4 electrons per count. Then the conversion from electrons to counts changes things:
mean (electrons) 16,000
mean (counts) = --------------- = ------------ = 4,000
electrons/count 4
stdev (electrons) 126
stdev (counts) = ----------------- = ------------ = 32
electrons/count 4
Now, because of the gain factor, the standard deviation of the number of counts per pixel is NOT the same as the sqrt of the number of counts:
stdev (counts) = 32
sqrt (mean counts) = sqrt(4,000) = 64
In fact, you can see that we can figure out the gain by looking at the statistics of the counts:
2
[ sqrt(mean counts) ]
gain = [ ----------------- ]
[ stdev (counts) ]
However, this simple method only works if there are no sources of noise in the CCD, so that the number of electrons is given exactly by photon statistics. Any real CCD has several sources of noise, so this technique won't yield precise results (though it ought to get in the ballpark).
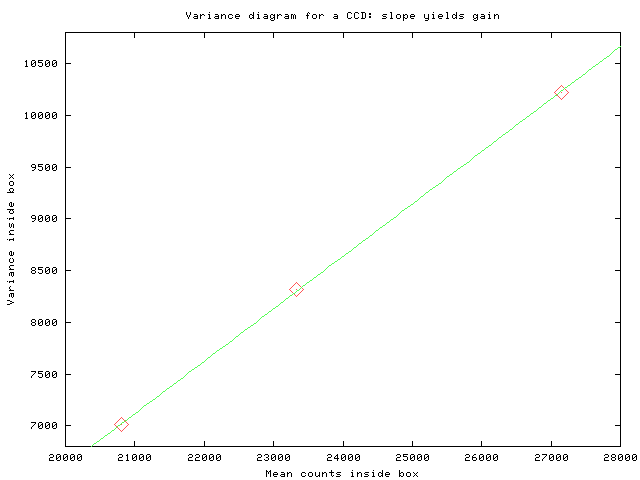
A better way to measure the gain is to use pairs of flatfield exposures at different signal levels. The idea is to measure the signal and variance of counts in several pairs of images, at different light levels, and then make a plot of variance vs. signal. In brief, here's how to do it. There's a detailed, step-by-step guide available showing how to use the XVista commands to carry out the operations.

Exercise:
- Using several pairs of flatfield frames from Apr 11, 2002, and a small box of about 50 x 50 pixels, determine the gain of the RIT CCD camera.
- How close is it to the value stated in the FITS header?
For more details on measuring the gain of a CCD camera, see
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.