 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Analyzing dark frames from Sep 25, 2003
On UT Sep 25, 2003, we placed the SBIG ST-9 CCD camera onto the
16-inch telescope and acquired a set of "dark" images -- that is,
images taken with the shutter closed. In theory, these images
should show nothing. But in practice, dark frames do contain
something: noise, due to thermal motions of silicon with the
chip's lattice. In order to remove this noise from a real
image, one must first understand its properties.
Today, you will
- display the dark images with the tv command
- define a subsection of the image with the box command
- compute the mean and stdev of pixel values within the
box via the mn and abx commands
- create histograms of pixel values via hist
- look at the histograms via xplot
- figure out the mean dark current for a "warm" and "cold" camera
Getting ready
First, make sure you have a copy of all the images in your
own sub-directory. Be sure to go to that sub-directory
as soon as you log in to iceberg, and do all your work there.
If you accidently delete or overwrite some images, let me know,
and I'll help you to get new copies.
Use the tv command to display images in the "warm" series:
dark1-001d.fit dark10-001d.fit dark20-001d.fit dark30-001.fit
- What can you tell about this series of images by just
looking at them, and moving the cursor around on the images?
Define a box
Display the 1-second dark image. Then type the command
box 1 int
You will be told to define a box by clicking and dragging ...

Make a box in the center of the image, roughly one-quarter of
the image width by one-quarter of the image high.
If you screw up or don't like the box you get, just repeat the
command. When done, you should be told exactly where your
box is:
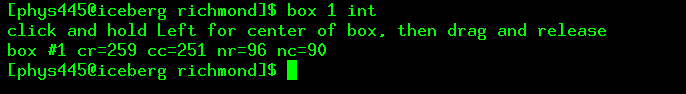
If you now type the command
box 1 show
the box you have just defined should appear on all open image windows.
It may disappear if the window is closed and reopened, or covered
and uncovered.
Boxes are useful to define subsections of images. It's often a good
idea to isolate a small section of an image for statistical purposes.
Computing image statistics
There are several commands for calculating statistics of
entire images, or subsections of images.
The mn and abx commands produce similar information


but the abx command is a bit more verbose.
- Use the mn command to calculate the mean and stdev
of pixel values within your box in the 1-second warm image
dark1-001d.fit. Write down the result.
- Repeat the measurements on other warm images: a 10-second image,
a 20-second image, a 30-second image. Again, write down
the results, making a small, neat table.
- Plot your data on the graph paper provided.
Place exposure time (in seconds) on the horizontal axis,
and mean pixel value (in counts) on the vertical axis.
- Determine the slope and y-intercept of the
line defined by your measurements.
Explain the units and meaning of the slope,
and the units and meaning of the y-intercept.
Making histograms of pixel values
The mean and stdev are nice, but they don't always tell
the whole story.
You can learn more about the properties of an image
by making a histogram of pixel values;
that is, finding out exactly how many pixels have a value
of 100 counts, how many with 101 counts, how many with 102
counts, etc.
You can use the command hist to do the job for you, like so:
hist dark1-001d.fit box=1
By running this command on an image, you will create a data file
which has the same name as the image, but with an extension of ".his"
instead of ".fit".
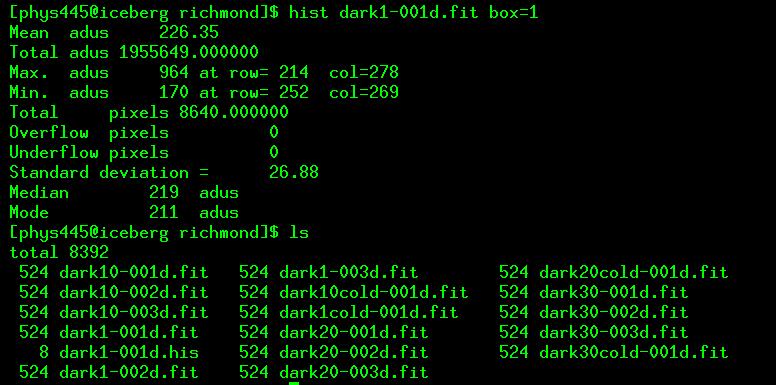
What does this ".his" file contain? A simple 2-column list of data,
in which the first column represents a pixel value, and the
second column the number of pixels in the image (or sub-image)
which have that value. You can look at the values
with the Unix command more:
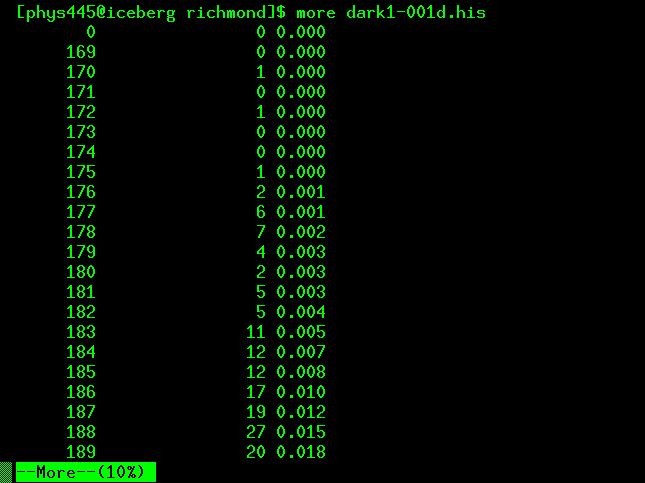
But you can understand this more simply by making a graph.
The
XVista
package contains a quick-n-dirty plotting program called xplot.
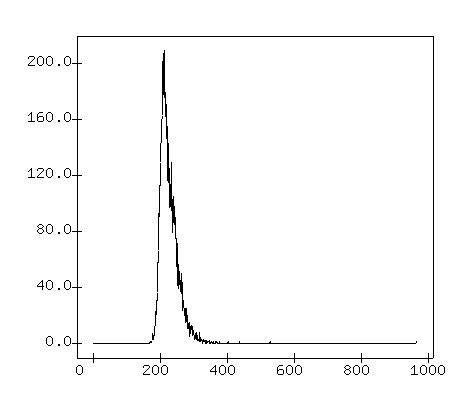
You can use it like so:

When you run the program, it should pop up a new window, inside
which it should draw a graph like this:
You can quit the xplot program by typing "quit" to its
command prompt.
- Run the hist program on one each of the
1, 10, 20, 30 second warm images
- Use the xplot program to make a graph of the distribution
- Describe each graph. Do you see any common features?
- Do the statistics "mean" and "stdev" describe this
distribution accurately? Explain.
The importance of temperature
Okay, you should know quite a bit about the
warm images now. The camera had a temperature
of around 23 degrees Celsius during these exposures.
But we also took a set of images at a temperature
of around -20 degrees C.
Do the images look any different?
- Display side-by-side one of the 30-second warm images,
and the 30-second cold image.
- Aside from the mean level of each image,
do you see any obvious differences in the appearance of the
two images?
Is the "dark current" any different in the cold images?
- Using the same box as before,
measure the mean and stdev of pixel values
in the 1, 10, 20, 30 second exposures of the "cold" series.
- Graph these data on a second piece of graph paper
- Determine the slope and y-intercept of these data
- Compare the slopes and y-intercepts of the "warm" and "cold" series
Now use the hist program to examine the distribution of pixel
values for the "cold" images.
- What features do you see in these distributions?
- Do the "warm" and "cold" distributions look similar or different?
Explain.
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.

 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.

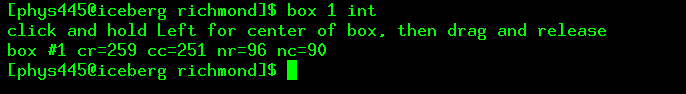
![]()





 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.