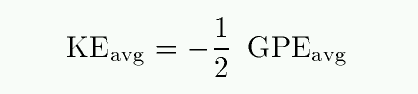
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
The two-body problem is solved: given a reasonable amount of information, we can determine exactly the mass of each component. But what about systems with more than two bodies? The three-body problem has analytic solutions in a very few restricted cases; but the N-body problem resists all exact solutions. Rats.
Nonetheless, even for groups of hundreds or thousands of stars, there are a few overall properties which yield to a bit of cleverness. For example, if we make some reasonable assumptions, we can find the total mass of the system with the help of the virial theorem.
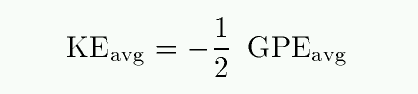
In order to use the virial theorem, we need to make some assumptions. The following must be true, or our results will incur systematic errors.
- The system is in equilibrium
- In order for the simple relationship between kinetic and gravitational potential energy to hold, the system must be -- on average -- in a stable state. Individual bodies may be falling inwards, or flying outwards, or circling around the center of mass; but a roughly equal number must be moving inwards and outwards. If a majority of the stars were to move outwards together, in sync, or if the cluster were gravitationally unbound, then we could not apply the virial theorem.
In addition, if the following conditions are true, the calculations become even simpler.
- All bodies have the same mass
- The (few) bodies which you measure are truly representative of the (many) in the system
- The system is not rotating
- If it were rotating, one would have to include terms for centrifugal energy.
A globular cluster is a collection of tens of thousands to hundreds of thousands of stars, all orbiting around their common center of mass, packed within a region several parsecs in radius.
Globular clusters orbit our Milky Way Galaxy (and other galaxies) like moons going around a planet. There are over one hundred globular clusters known to circle the Milky Way. Some really giant galaxies are surrounded by thousands of these fuzzy balls of stars. For example, look at all the little spots of light around the giant elliptical galaxy M87:
Most of those spots are globular clusters. We can pick out even more by zooming into the center of the galaxy and subtracting a smooth model of the galaxy:
One of the clusters in our own galaxy was first noticed by French comet hunter Charles Messier. He made it the object number 71 in his list of comet-like celestial sources; hence its common name, M71.
Image courtesy of
T. Credner, S. Kohle, University of Bonn
Astronomers Ruth Peterson and David Latham picked out several of the brightest stars in this cluster. They sent the light from each star, one at a time, through a spectrograph, measured their radial velocities. Consider this list of measurements from their Table 1.
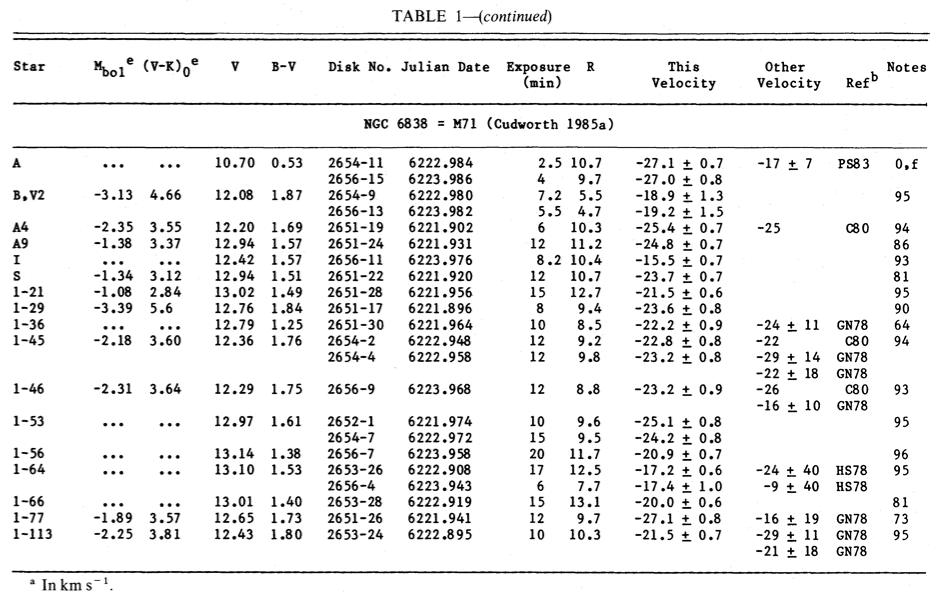
Exercise:
- What is the average radial velocity of these stars?
- What is the standard deviation from the mean?
The average velocity is -- if these are representative of the cluster as a whole -- the speed of the center of mass of the entire cluster, relative to the Sun. We call this the systemic velocity.
The second value is usually called the velocity dispersion, and denoted by the symbol sigma (σ). We can use the velocity dispersion of a cluster to estimate its mass via the virial theorem. The average value of the 1-D velocity squared -- in the radial direction -- is
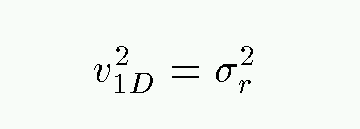
Now, if the motions of the stars in the cluster are isotropic, then there is nothing special about the direction towards Earth; that means that the true, 3-D velocities of the stars in the cluster have an average squared value
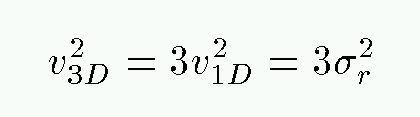
If the cluster were rotating, then the velocities would not be isotropic: there would be a preferred direction, perpendicular to the axis of rotation. In that case, the average 3-D velocity squared would not be exactly 3 times the square of the measured velocity dispersion, but some other factor; maybe 1.2, maybe 2.5. The order of magnitude would be the same, but the exact value would not.
Returning to the virial theorem,
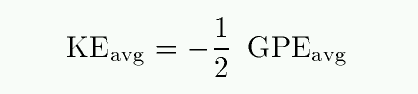
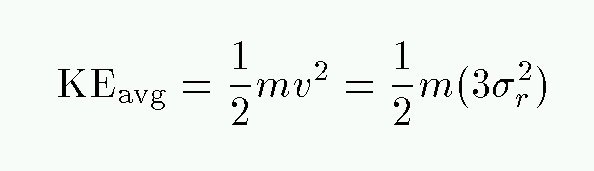
Can we find an expression for the average gravitational potential energy of a typical star? Well, if we assume that the entire cluster has mass M, then the GPE will be something like
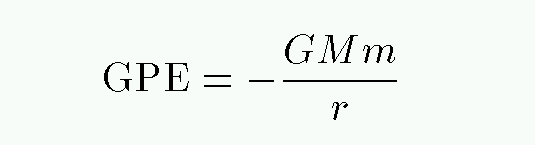
But what is the typical distance between the center of mass and an average star? It's probably something like half the radius of the cluster R. In that case,
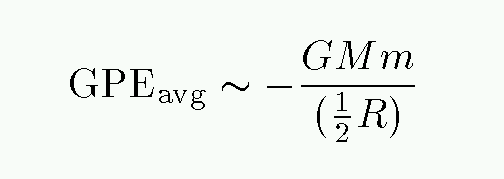
So, putting it all together, we have
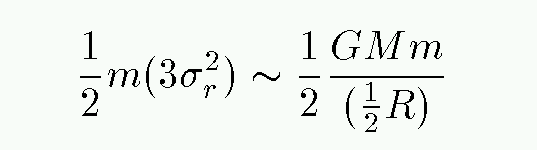
Exercise:
- Solve for the mass of the cluster M in terms of the other variables.
In the case of M71, what is the radius of the cluster R? The distance to M71 is roughly D = 3.8 kpc, and you can use this portion of the DSS provided by Aladin to estimate the angular radius of the cluster:
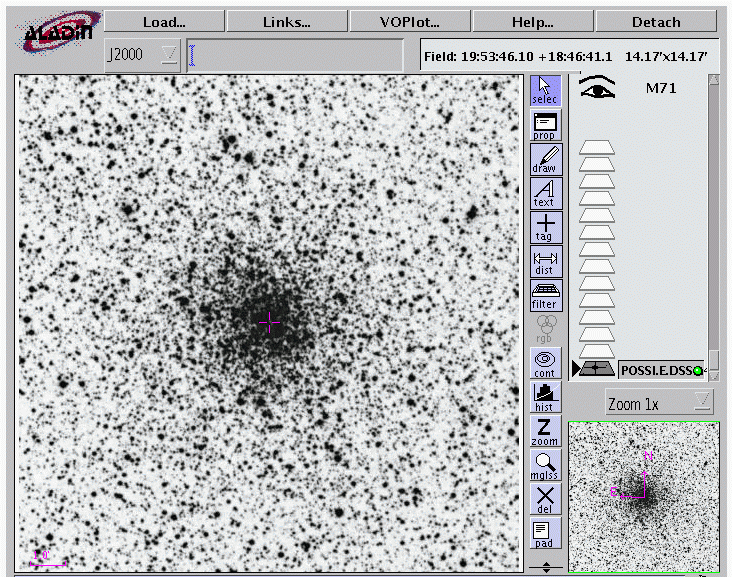
Exercise:
- Estimate the radius of M71, in pc.
- Use the virial theorem to estimate the mass of the cluster, in solar masses.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
