Cleaning Target Images and Determining their Properties

Today, you will

apply the master dark and flatfield frames to a raw target image (to make a "clean" image)
determine the orientation and plate scale of a target image
determine the FWHM of a target image

Cleaning a target image

In order to turn a raw image into one which accurately reflects the amount of light which struck each pixel, you need to "clean" it. There are two steps involved in cleaning our images of asteroid Lictoria:

subtract the master dark
divide by the master flatfield

First, copy a raw target frame into your directory:

      cd
      cp mar30_2002/1107a.001 richmond
      cd richmond

Next, do the dark subtraction

make a copy of the raw image
```
      cp 1107a.001 copya.001
```
display the raw image, using parameters z=750 l=300 xo=500. Leave the window alive and open.
subtract the master 15-second dark frame from the image
```
      sub 1107a.001 dark15.fts
```
display the dark-subtracted image, using parameters z=570 l=300
compare the two images, which should be sitting side-by-side.

Now, do the flatfielding

kill the raw image window, but leave the dark-subtracted image window alive
We need to know the mean value of the master V-band flatfield frame in order to place the target frame back to its original mean level after we divide by the master flatfield. So, calculate the mean value of the master V-band flatfield frame
```
      mn flatv.fts 
```
divide the dark-subtracted frame by the master V-band flatfield. Note the flat keyword at the end of the command -- it uses the mean of the flatfield frame (which you just calculated) to rescale the frame to its original mean level.
```
      div 1107a.001 flatv.fts flat
```
display the flatfielded image beside the dark-subtracted image
compare the flatfielded and un-flatfielded image. Do you see any difference?

Congratulations! The file 1107a.001 should be at this point nice and clean. The pixel values in the image should now represent fairly the amount of light which struck the CCD.

Determine the plate scale and orientation

Your clean image isn't very meaningful unless you know which way is North, which way is East, how big the field of view is, and so forth. You need to determine the plate scale (arcsec per pixel) and orientation. Once you know these parameters for one image, you'll know them for all the images taken during a night (and, usually, all the images taken with the same telescope and camera).

The image 1107a.001 was taken on the night of March 30, 2002. The time of the exposure is recorded in Eastern Standard Time in the FITS header. Use the buffers command to look it up. Then convert to Universal Time.

Look up the location of the asteroid 1107 Lictoria at the time and date of the exposure, using the JPL Ephemeris site. Make a finding chart using the Aladin tool.

Match the finding chart to the displayed image. Which way is North? Which way is East?

Exercise:

Make a picture of the image window with the directions labelled, something like this:

                    -----------------
                    |     North     |
                    |               |
                    |West      East |
                    |               |
                    |     South     |
                    -----------------

Next, you must figure out how many arcseconds per pixel in the image. Use the Aladin tool's Vizier option to display an overlay for stars in the USNO catalog. The Dist button will show you the distance between any two stars. Pick two reasonably bright stars which appear both in the finding chart and in the image.

Find the distance between the stars in the finding chart. Convert from arcminutes to arcseconds.
Find the distance between the stars in the image, in the row and col directions. Use the Pythagorean equation to calculate the total distance in pixels.
Calculate the number of arcseconds per pixel.

Compare your answer to that of other students. You should all get the same answer...

You can check your result: if you know the focal length of a telescope and the physical size of each pixel in a detector, you can calculate the pixel scale via

                                             -1  ( pixel size D  )
      angle subtended by each pixel   =   sin    (---------------)
                                                 ( focal length L)

Exercises:

Look up the size of pixels in a Kodak KAF-1600 CCD chip
Calculate the focal length of the Meade 10-inch telescope with an f/6.3 focal reducer
Calculate the expected pixel scale
How does this compare to the actual pixel scale?

Determine the FWHM of the PSF

One measure of an image is the shape and size of the Point Spread Function (PSF). If the telescope is focused properly and the atmosphere is stable, stars will appear to be tiny little round points of light. But if the telescope isn't focused, or the air is turbulent, stars will appear as fuzzy blobs. The more area over which a star's light is spread, the harder it is to measure precisely.

The conventional way to measure the size of a PSF is by its diameter at a level of half the maximum pixel value:

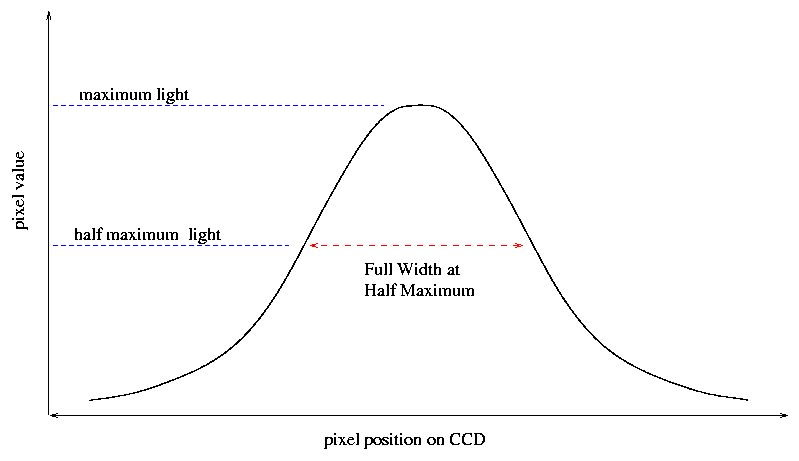
This FWHM is roughly the same for all the stars in an image, bright and faint alike. The smaller the PSF, in general, the better one can measure stellar properties.

Yes, yes, if the FWHM is much less than two pixels, then the sources aren't properly sampled.

Good astronomical sites, located high on mountaintops where the airflow is laminar, routinely record FWHM values of less than one arcsecond. Telescopes in space have a FWHM set by diffraction.

You can use XVista's tv window to find the FWHM of stellar sources in an image, in two ways:

Method one:

display an image
determine the background level in the image
move the cursor to a star, placing it just to the left of the visible extent of the star
using the arrow keys, march the cursor one pixel at a time to the right, across the stellar image

make a table which shows the pixel values as you go:

        row     col       pixel value       pixel - background
       --------------------------------------------------------

find the location of the peak pixel value, and the value of (peak pixel - background)
how many pixels must you go away from the peak for the (pixel - background) to fall to half its peak level?
write down the FWHM, in pixels

Method two:

display an image
move the cursor to a star of interest
press the "r" key -- a new window should pop up showing the radial profile of the star under the cursor (if the new window is all black, press the "r" key again)

This radial profile shows the (pixel - background) values on the Y-axis, and the distance of each pixel from the center of the star on the X-axis. The program fits a gaussian curve to the data, and plots the fit as a solid line. It prints the parameters of the fitted gaussian at the top of the window: central row, central column, FWHM, eccentricity.

Repeat both methods to find the FWHM of two bright stars and two faint stars.

Exercises:

How does your values compare to the values found by XVista?
Convert XVista's average value of FWHM from units of pixels to units of arcseconds.
Is the RIT Observatory at a good site?