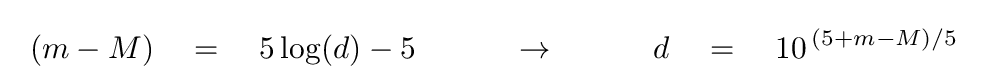Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Using supernovae as distance indicators: Type Ia version
This time, we examine supernovae which involve the accretion of
material onto a white dwarf star until it explodes;
these are called "Type Ia" events.
To first order, these supernovae appear to be a very
homogeneous group,
and so for years it was hoped that they might serve as
standard candles.
Recent developments have shown that it may take a bit
more work to choose a proper subset of them,
but that the idea is still a good one.
Let's review the nature of Type Ia supernovae.
We believe there are two ways that a white dwarf
might be induced to explode.
- Single degenerate
-
The most common explanation starts with
binary-star systems in which an ordinary
main sequence star orbits close to a carbon-oxygen white dwarf.

Image and animation courtesy of
ESO/M. Kornmesser
Material from the main-sequence star can -- under the right
circumstances -- escape from the outer atmosphere
and form an accretion disk around the white dwarf.
If the rate of mass accretion onto the white dwarf falls
into the proper range,
then the white dwarf's mass may eventually reach
the Chandrasekhar limit, about 1.4 solar masses.
At that point, little regions of thermonuclear reactions near the
center of the white dwarf may enter a runaway
instability,
turning most of the white dwarf from C-O to Fe-group
elements and producing enough energy to blow the entire
white dwarf into smithereens, which fly out into space at
very high speeds.
The main sequence star, on the other hand, survives the explosion,
though it takes a lot of damage.
- Double degenerate
-
Well, that's one possibility. Another is that TWO white dwarfs
in a close orbit may eventually merge
(the double degenerate scenario).
The merger creates a single object which again exceeds
the Chandrasekhar limit, and, once again,
Ka-Boom.

Image courtesy of
NASA/CXC/M.Weiss
In this case,
both of the merging white dwarfs are completely destroyed,
so there is no surviving star.
-
In both of these scenarios,
the result is pretty similar:
the body of one (or two) white dwarf(s)
blows apart into a cloud of gas,
which is heated to temperatures of around 100,000 Kelvin
and sent flying outward at speeds
of 5,000 to 10,000 km/s.
The hot cloud radiates light at all wavelengths,
growing brighter as it increases in size
over the first few days or weeks.
But wait -- there's a bit more to it than
just a hot cloud of expanding gas.
The nuclear reactions which caused this
explosion converted a good portion of the white dwarf's
material into a few isotopes of iron (Fe) and nickel (Ni).
Most of these isotopes are unstable and decay
over the next few days or weeks,
injecting energy into the cloud.
In particular, the decay chain
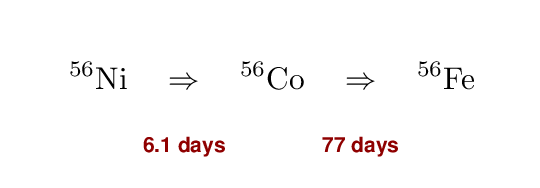
produces a significant portion of the energy
which eventually turns into (mostly) visible light.
This energy, released over a relatively prolonged period of time,
is responsible in large part for the characteristic
shape of a Type Ia light curve.
Based in part on data taken at the RIT Observatory,
figure taken from
Richmond and Smith, JAVSO, 40, 872 (2012)
If all Type Ia supernovae were identical,
producing the same luminosity and decaying over the same period,
then we could treat them as
standard candles.
In that case,
we could
- measure the absolute magnitude M of a few nearby examples
(using other techniques such as Tully-Fisher or
TRGB to determine the distance to their host galaxies)
- measure the apparent magnitude m of many other events
- compute the distance to each Type Ia using the distance modulus
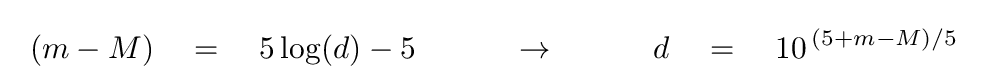
In the Old Days (1970s and 1980s),
the collection of measurements was relatively small
and inhomogeneous. At that time,
it seemed possible -- within the uncertainties --
that all Type Ia SNe did indeed have the same absolute luminosity;
in other words, it seemed possible that they
might be standard candles.

Abstract from
Branch and Bettis, AJ 83, 224 (1978)
However, as astronomers accumulated better
measurements and larger samples, it became clear
that SNe Ia are not all identical.
These supernovae
appear to vary in a systematic way.
For example, if we measure the amount by which
supernovae decline in brightness 15 days
after maximum light in the B-band,
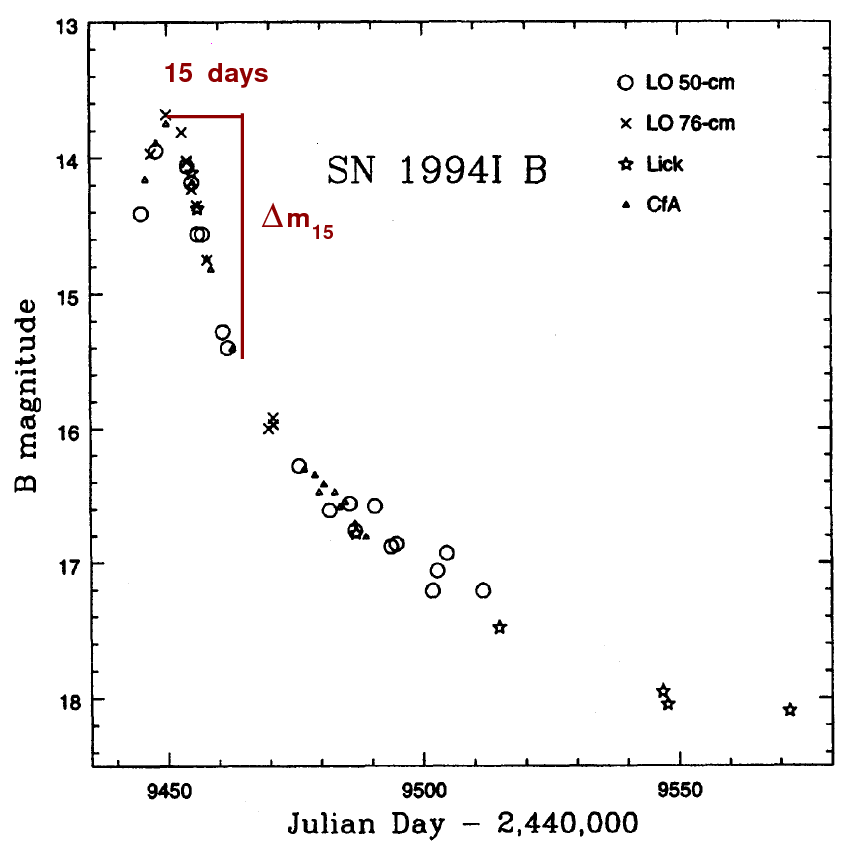
Figure taken from
Richmond et al., AJ 111, 327 (1996)
and compare it to the absolute magnitude of the
event,
we find a clear correlation.
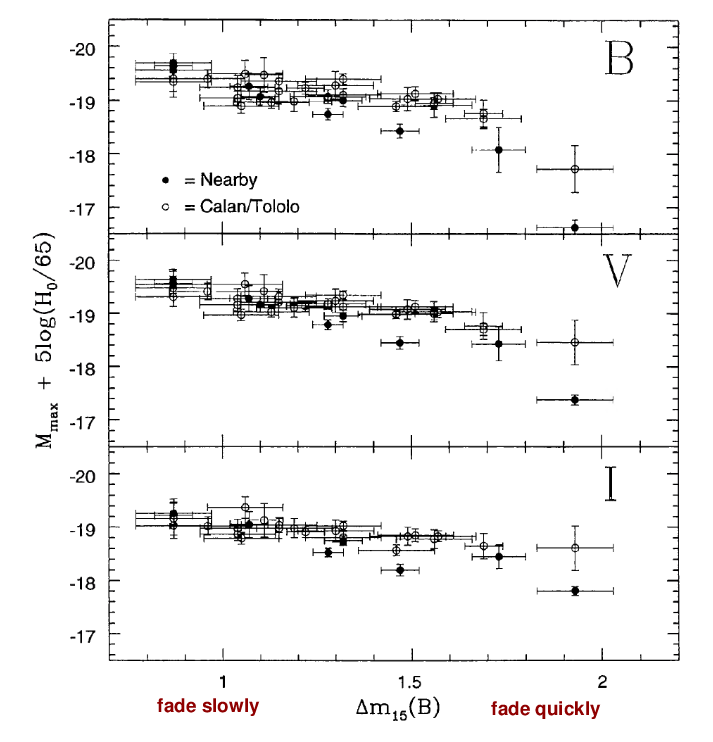
Figure 2 modified from from
Hamuy et al., AJ 112, 2391 (1996)
Extraluminous Normal Subluminous
-----------------------------------------------------
decline slowly decline quickly
bluer redder
faster ejecta slower ejecta
-----------------------------------------------------
If we can measure enough SNe Ia to pin down these
relationships between absolute magnitude
and other observable quantities,
we can perhaps turn SNe Ia into
standard-izable candles;
not as nice as truly standard candles,
but still useful.
There are several groups working on this problem,
with slightly different techniques,
and both have found some success.
The SALT procedure involves choosing one of
a set of templates which best fits the light curve
of some particular observed SN Ia.
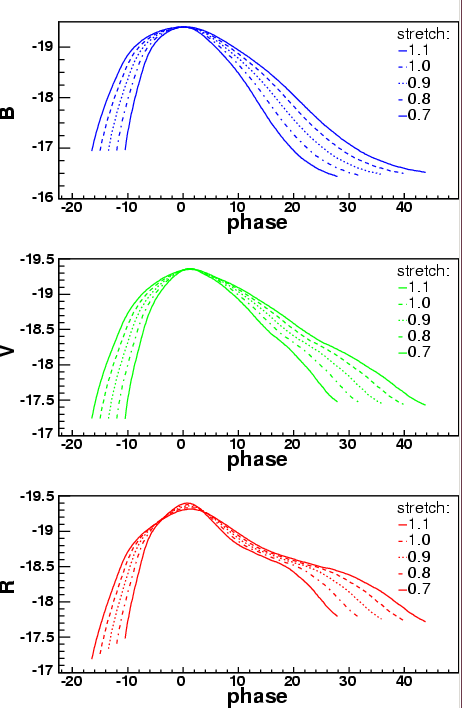
Figure taken from
Guy et al., A&A 443, 781 (2005)
Using these methods to correct for the
relationship between decline rate and
luminosity,
one can reduce the uncertainty in
distance modulus measurements for SNe Ia
to perhaps
0.15 magnitudes.
Q: If the uncertainty in absolute magnitude
is +/- 0.15 magnitudes, what is the
uncertainty in distance?
Express as a percentage.
If one looks at SNe in the near-infrared H-band,
they may indeed be nearly identical;
the Hubble diagram below uses measurements
which have NOT been corrected for the
decline-rate effect.
To be fair, much less work has been done in the
near-IR than in the optical.
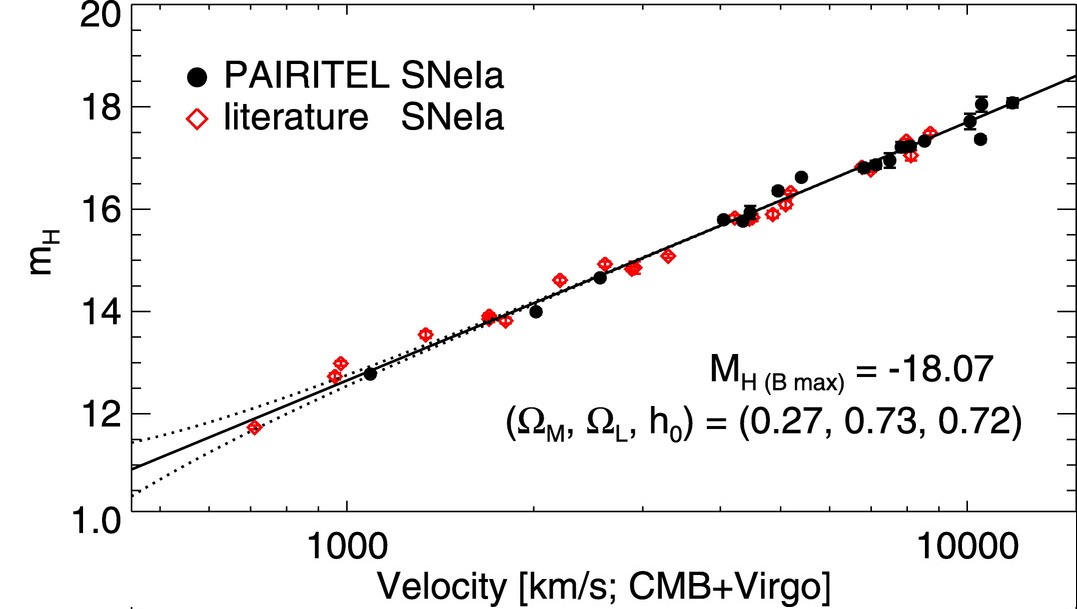
Figure taken from
Wood-Vasey et al., ApJ 689, 377 (2008)
One of the reasons
astronomers spend so much time trying to understand
Type Ia SNe is that they are really, really
luminous: their absolute magnitudes
are around -19 or -20!
That means that they can be seen at VERY large
distances,
which means that they may be able to test
different cosmological models.
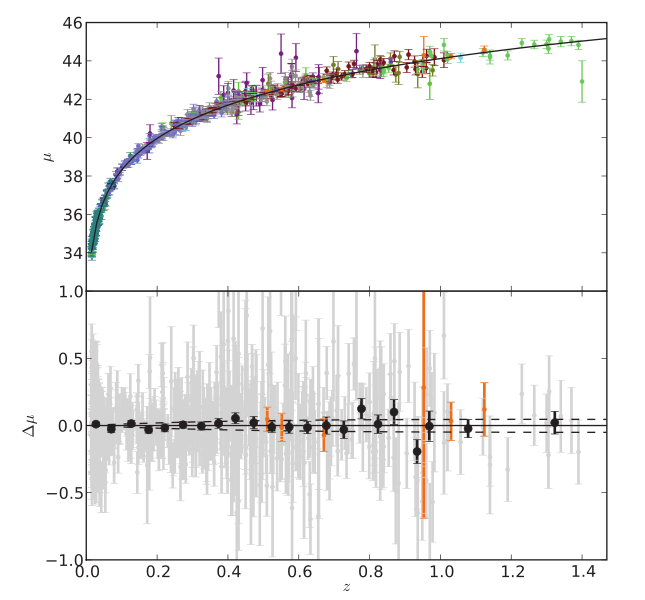
Figure taken from
Amanullah et al., ApJ 716, 712 (2010)
Q: What is the largest redshift out to which
SNe Ia have been detected, as shown in
the figure above?
What is the distance modulus to that
location? Just look at vertical axis.
To what (luminosity) distance, in Mpc, does that
correspond?
If you have a network device,
go to Ned Wright's Cosmology Calculator
and look it up.
If you don't, use the definition
of distance modulus.
Let's give it a try!
Our target will be SN 2011fe in M101,
which is one of the "good" Type Ia supernovae
for distance measurements:
- it suffered little extinction by interstellar material in its host galaxy
or in the Milky Way
- it showed the
"typical" or "normal" spectral features
- it was discovered very soon after the explosion
and measured frequently in several optical passbands
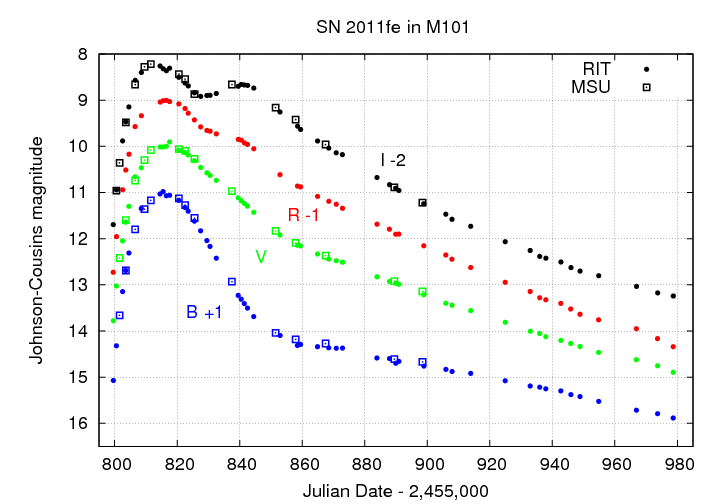
A portion of the B-band light curve measured by
Richmond and Smith, JAVSO 40, 872 (2012)
is shown in the figure below.
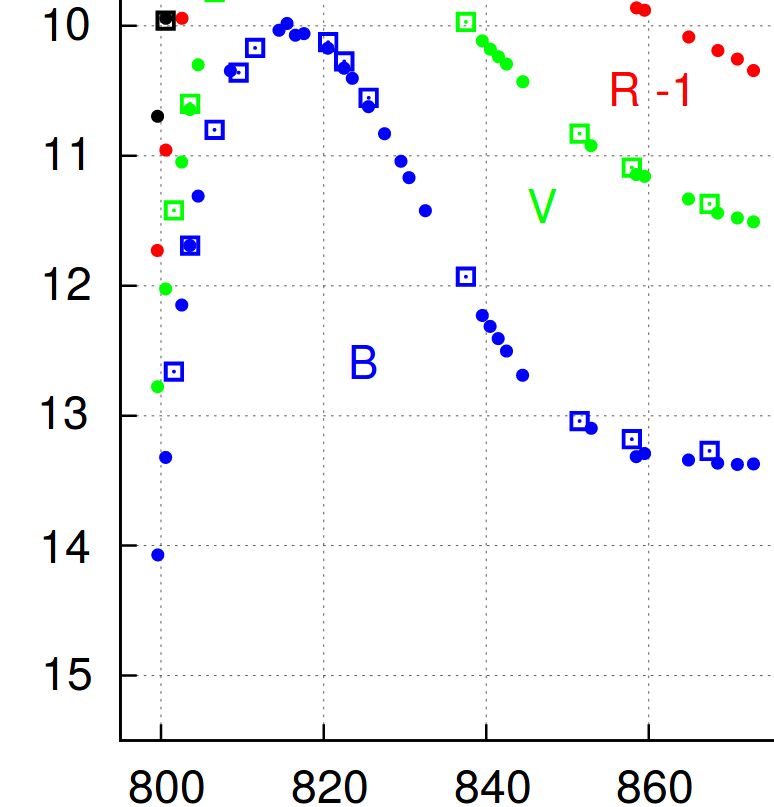
Modified slightly from Figure 3 of
Richmond and Smith, JAVSO 40, 872 (2012)
Q: What is the apparent B-band magnitude at peak?
Q: What is the Δm15 value in the B-band?
(how much does the magnitude fade in the 15 days after peak?)
Q: Use the relationship between decline rate and absolute magnitude
as quantified by Prieto, Rest and Suntzeff, ApJ 647 (2006)
MB = -19.325 + 0.636 ( Δm15 - 1.1)
to compute the absolute B-band magnitude of this event.
Q: Compute the distance to this galaxy.
You can compare your distance to those derived
using other techniques:
Now, one last word on Type Ia SNe:
even the "good" events only provide
relative distances.
If we account for the relationship between decline rate
and luminosity,
we can determine the distance of one SN to another ---
but we need to know the absolute
distance to the first SN to turn these ratios of distance
into Mpc.
This makes Type Ia SNe one of the "secondary" distance
indicators;
or, more accurately,
a "tertiary" indicator.
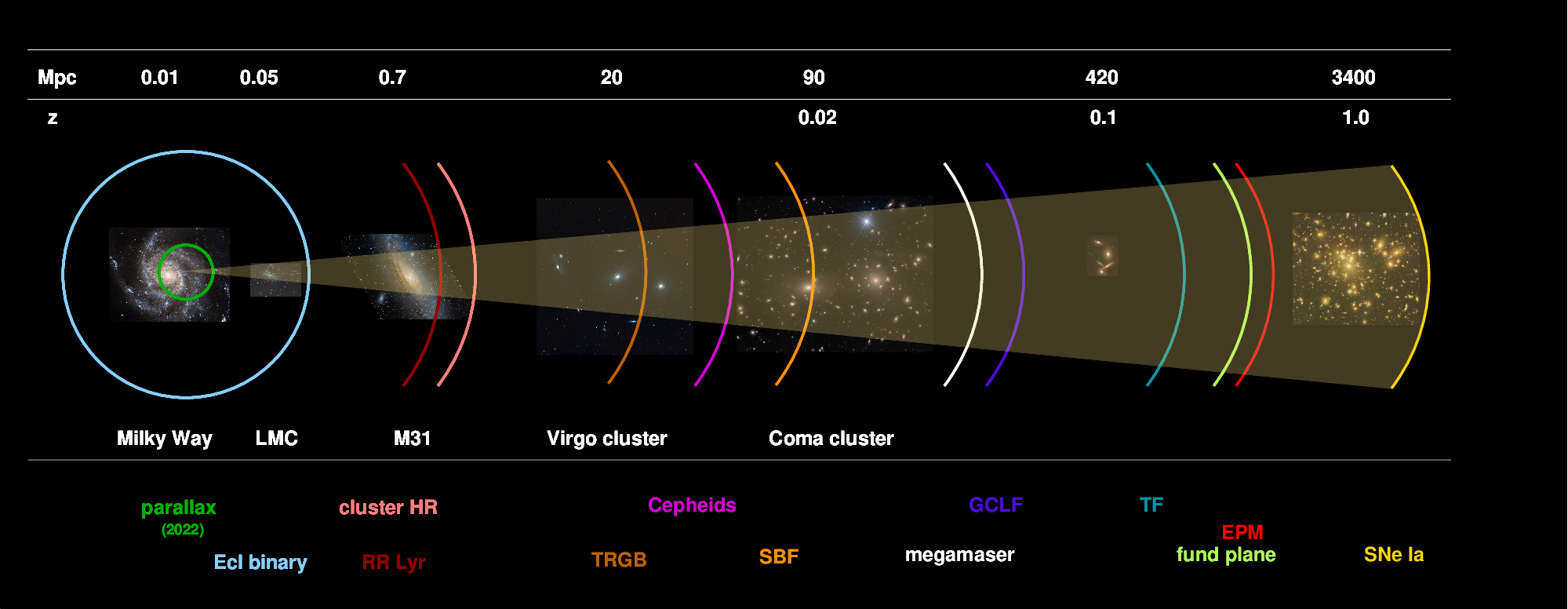
The problem is these explosions
are so uncommon that we haven't seen
many (or any) in regions of space close enough
to be reached with parallax,
or even with some other methods.
So we need at least 3 steps:
- parallax, with which we can reach ...
- RR Lyr or TRGB or Cepheids, with which we can reach ...
- Type Ia SNe
Still, even with this caveat,
type Ia supernovae provide a powerful tool,
because we can see them (and measure their properties)
SO FAR AWAY!
- A good recent review article describing supernovae and their
use as distance indicators is
- Would you like to help find supernovae? You could join the
-
Short video explaining Type Ia SNe
from NASA's Nancy Roman Grace Space Telescope site
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.


 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.