Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
How can we measure the mass of a galaxy? Although there are a myriad of different techniques, one can divide them into two broad categories:
Q: Which of these two approaches is more reliable? Q: Why?
In my mind, the second approach is the better one, simply because we might fail to detect some important component of a galaxy's mass budget. For example, before X-ray telescopes were devised, astronomers could not detect the very hot gas which fills the space within galaxy clusters; and that gas turns out to contain more mass, in many cases, then the visible stars in all the galaxies combined.
Just how can one figure out the amount of mass in a galaxy from the motions of objects within it? That sounds pretty complicated. Let's start with a simple situation in order to see the basic idea.
Our Solar System consists of
In this case, almost all the mass resides in one object, the Sun, which sits at the center of the system.
Graph courtesy of
Das steinerne Herz and Wikimedia
For our purposes, we can ignore all the gravitational interactions which don't involve the Sun. That means that the motion of every planet is very simple, due only to the gravitational force of the Sun.
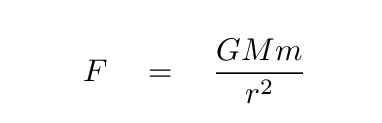
For objects in circular orbits, we can equate the centripetal force on the object to the gravitational force from the Sun.
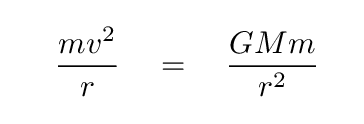
Q: Can you solve this equation for the velocity as a function
of radius?
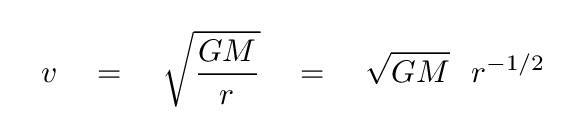
When we measure the speeds of planets and asteroids in our Solar System, we find exactly this sort of relationship. It is often called "Keplerian motion", as it is consistent with the rules Johannes Kepler described in his work.
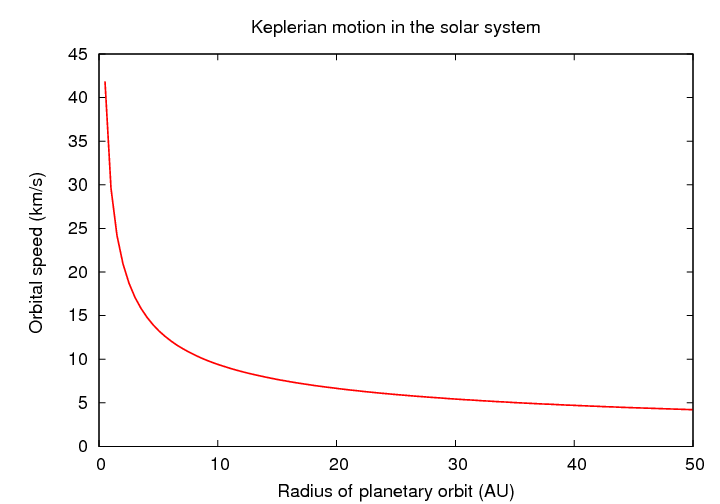
Notice how quickly the orbital speeds decrease with radius.
In order to apply this method to determine the mass of the Milky Way Galaxy, we need measure the motions of objects within it. There are quite a few possible types of objects we might use as tracers of the gravitational force (or gravitational potential).
If we ASSUME that some particular object is moving in a circular orbit, then all we need is its location in the Galaxy (position on the sky and distance), and its radial velocity. That's not too hard. But if the orbit is not circular, we need to measure all three components of its motion: not only the radial velocity, but also the transverse velocity. The latter is very hard to measure accurately, because even relatively nearby stars move by tiny amounts over human timescales. Fortunately, Gaia has come to the rescue: its instruments can provide precise values for the transverse motions of stars and clusters, as well as their distances.
Many astronomers have contributed to the effort over the past century. Let's look at at a recent example.
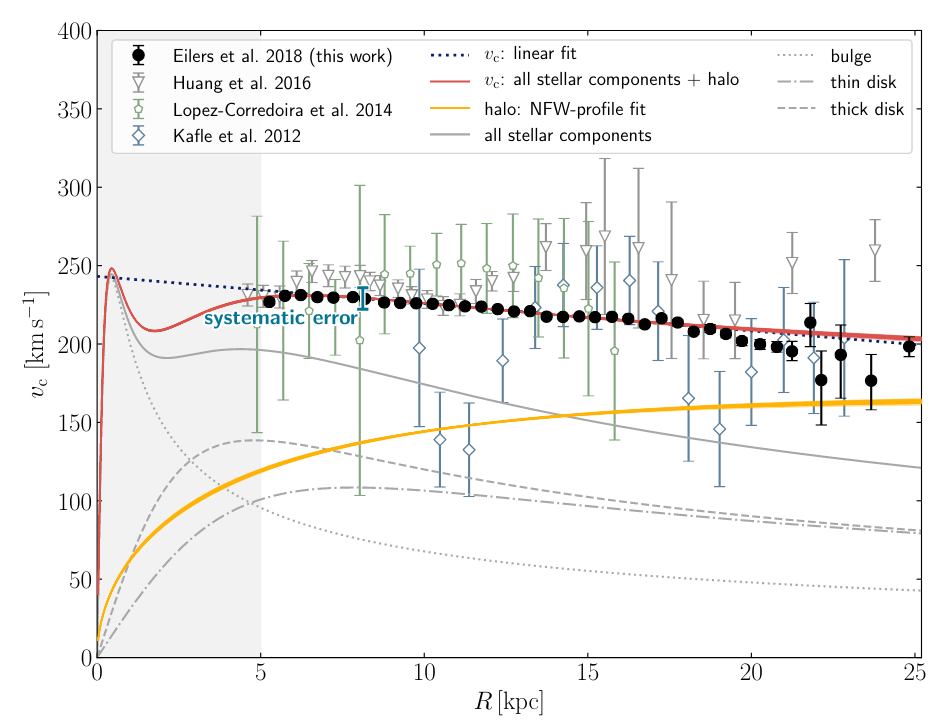
Figure 3 taken from
Eilers et al., ApJ 871, 120 (2019)
Q: Do the measurements decrease with a Keplerian pattern?
Q: If not, what does this mean about the distribution of mass
in the Milky Way
The rotation curve of the Milky Way does not decline quickly with radius, but is instead almost flat.
What does that mean? It means that the bulk of the mass CANNOT be concentrated at the center, but instead must be spread out more evenly throughout the galaxy.
Okay. We see evidence that a considerable amount of mass must be spread throughout the entire Milky Way. Can we be more specific? Is it possible to figure out how that mass is arranged?
The answer is "yes." The details are complicated, but we'll adopt a simple approximation for illustrative purposes. As Isaac Newton showed long ago,
The gravitational force at radius R due to a spherically symmetric distribution of matter is identical to that of the mass enclosed within R, all concentrated at a point at the center.
In other words, an object in a circular orbit of radius R will have a velocity given by
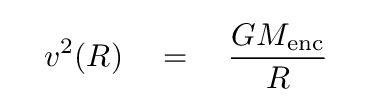
where the mass enclosed within radius R can be computed by the integral of the density over a series of spherical shells.
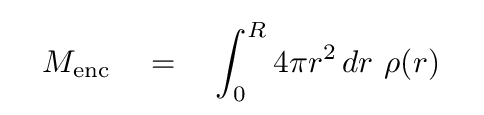
Using this approach, astronomers can estimate the mass of our Milky Way contained with a range of radii, and the derive the speed with which objects would move in circular orbits. Dealing with eccentric orbits is more complicated, so we'll leave that to the experts.
Let's practice with an example:
Q: Suppose that the density of a galaxy is constant --
the same at all radii. What sort of relationship
will we find for velocity as a function of radius?
Hmm. In that case, the circular velocity is proportional to the radius.
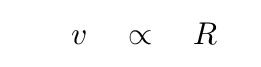
Hmmm. That doesn't sound right. That would mean that the velocity would rise and rise with greater distances from the center of the Milky Way; but that's NOT what we observe.
Figure 3 taken from
Eilers et al., ApJ 871, 120 (2019)
Just what sort of distribution of mass WOULD give rise to a flat-ish rotation curve? Let's assume that the density can be described as a power law of the radial distance:
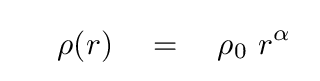
The mass enclosed within some radius R would then be
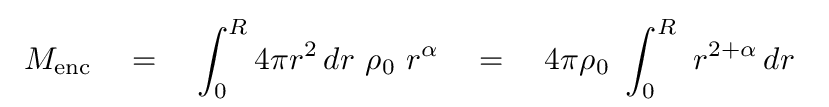
Q: How does the mass enclosed within radius R depend on R?
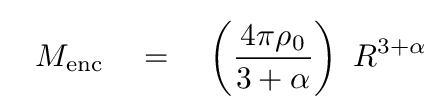
So, since this enclosed mass determines the circular velocity
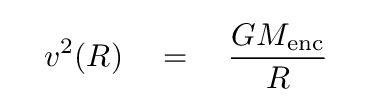
Q: What value of the density parameter α will lead
to a flat rotation curve?
Now, the rotation curve of our Milky Way is not _quite_ flat. If we want to make a more accurate estimate of the density, we can use velocities at various radii to estimate the mass enclosed at different locations. A recent review article combines results from many different studies and finds this relationship:
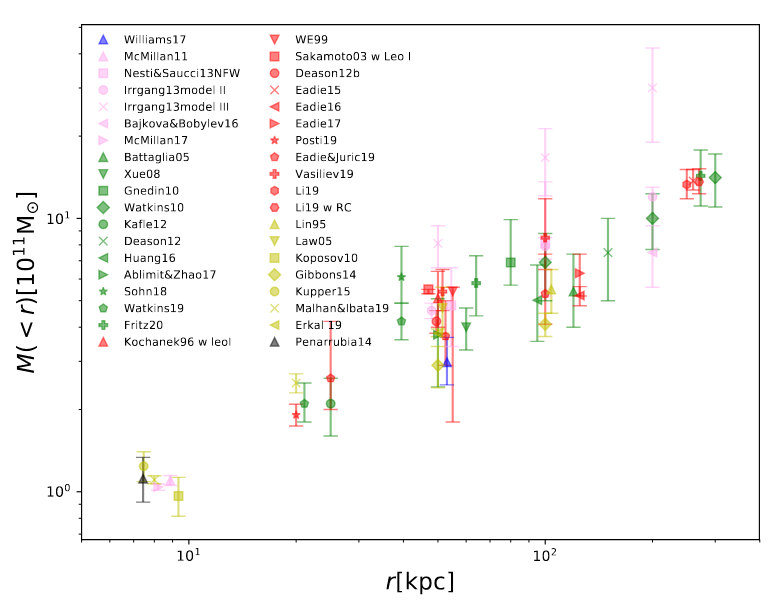
Taken from Figure 2 of
The mass of our Milky Way
by Wang et al., Science China Physics, 63, 0981 (2020)
Q: What is the logarithmic slope on this graph?
The logarithmic slope is equal to the exponent of the power law connecting two quantities, so measurements of the Milky Way indicate that the density of mass goes like
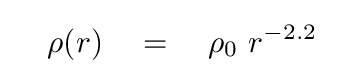
Well, good. That's not too far from the value of α = -2 which would produce a perfectly flat rotation curve.
We've been trying to figure out how MASS is distributed in our galaxy. But what about the LIGHT? Most galaxies are brighest at the center and fainter near the edges ... but exactly how does the light decrease with radius? If stars were the source of all light in a galaxy, and also the source of all mass, then we'd expect the distributions of light and mass to be very similar.
We can't really measure the luminosity of our own Galaxy as a function of radius, since we live inside it; but we can perform this measurement for other galaxies. The Andromeda Galaxy, for example, is thought to resemble our own Milky Way in many respects.
GALEX image of M31 courtesy of
NASA/JPL-Caltech
A graph of intensity of LIGHT as a function of radius shows a clear decrease ... but is it the same as the decline in density in our Milky Way?
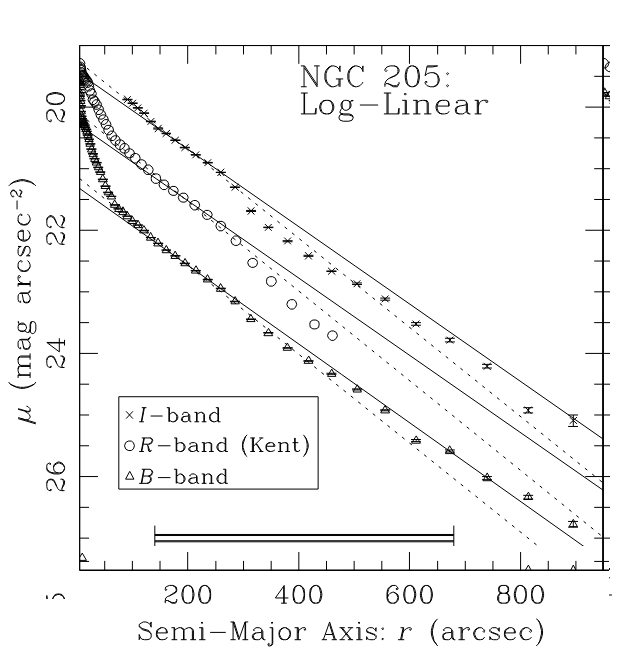
Image slightly modified from Fig 12 of
Tidal Interaction of M32 and NGC 205 with M31: Surface Photometry and Numerical Simulations
by Choi, Guhathakurta, and Johnston, AJ, 124, 310 (2002)
The data above clearly show that the surface brightness μ declines linearly with radius:
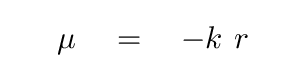
But surface brightness is measured in magnitudes per square arcsecond; and, as you may recall, magnitudes are a logarithmic function of the intensity of light.
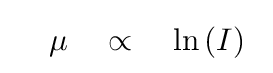
We therefore find that the INTENSITY of light decreases with radius, not as a power law, but as an exponential function.
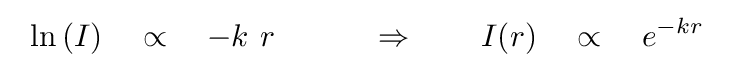
Q: Which falls off more rapidly: a negative power law, or
a negative exponential function?
Yes, exponential functions will eventually decrease more rapidly than power laws. This points to a very interesting, and non-intuitive, consequence:
In the outer regions of our Milky Way (and other galaxies), light decreases much more rapidly than mass; the light does not trace the mass. In other words, there is a lot of mass which does not emit light.
Hmmm. I wonder what we might call this mysterious substance which produces strong gravitational forces without emitting any light ....
Okay, fine. A recent review of many different methods finds pretty good agreement in the mass (measured in solar masses) interior to a certain very large radius called r200.
where r200 is defined as the radius at which the average density of a galaxy has fallen to 200 times the critical closure density of the universe.
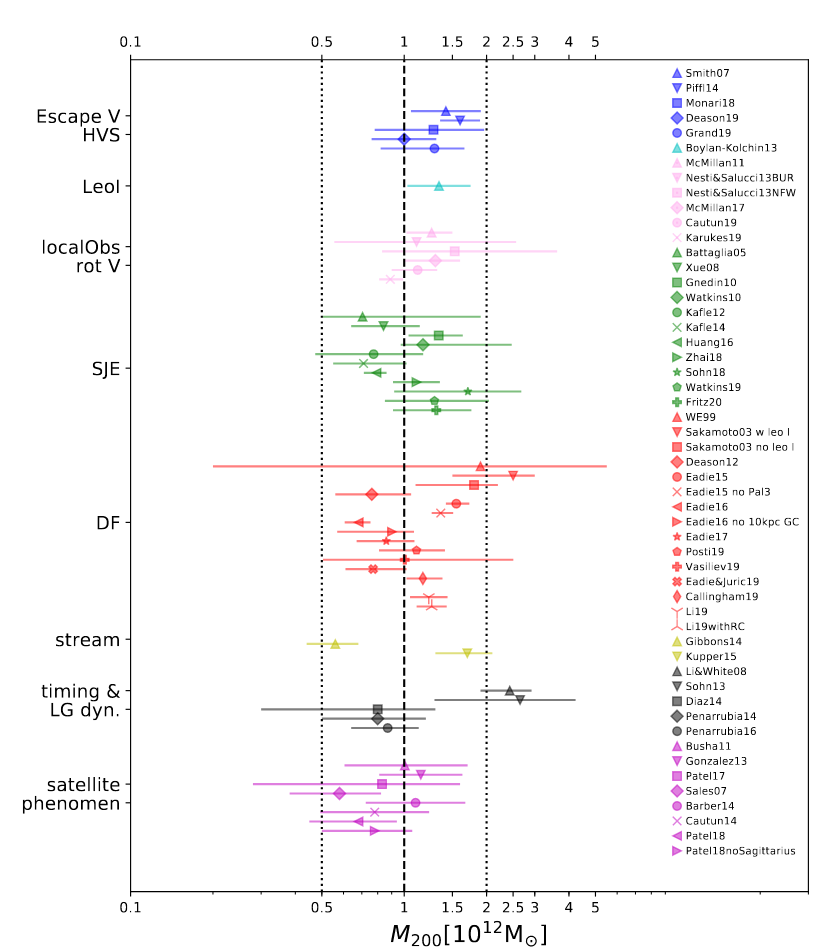
Taken from Figure 1 of
Cautun, M. et al., MNRAS 494, 4291 (2020)
Basically, out to this fiducial radius, the Milky Way contains roughly 1012 solar masses of material.
Notice that most of this mass lies in the far outer reaches, well beyond most of the light of stars.
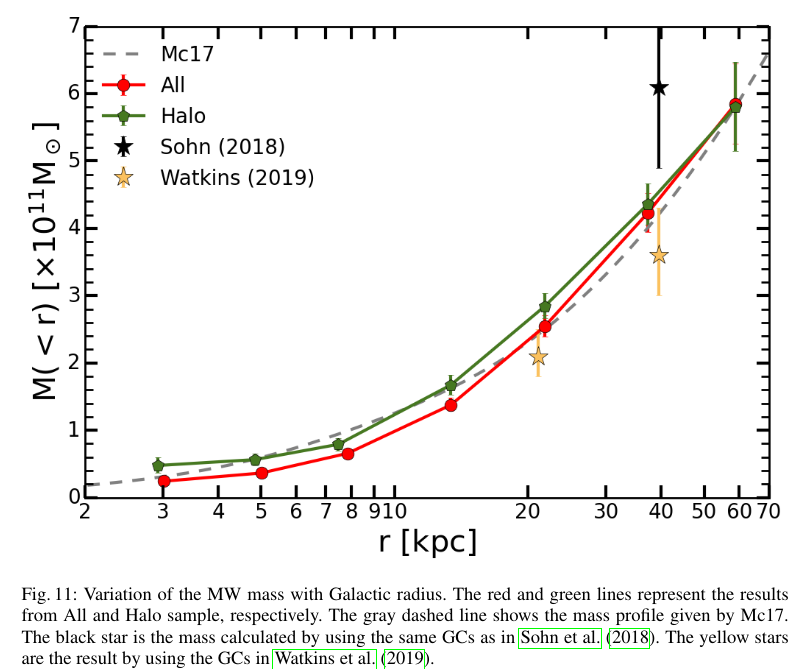
Image taken from Figure 11 of
Guangchen et al., Research in Astronomy and Astrophysics, 23, 5013 (2023)
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.