 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Imagine that you need to climb to the roof of your house. You don't have a ladder, but you do have a set of small pieces which could be used to make one.
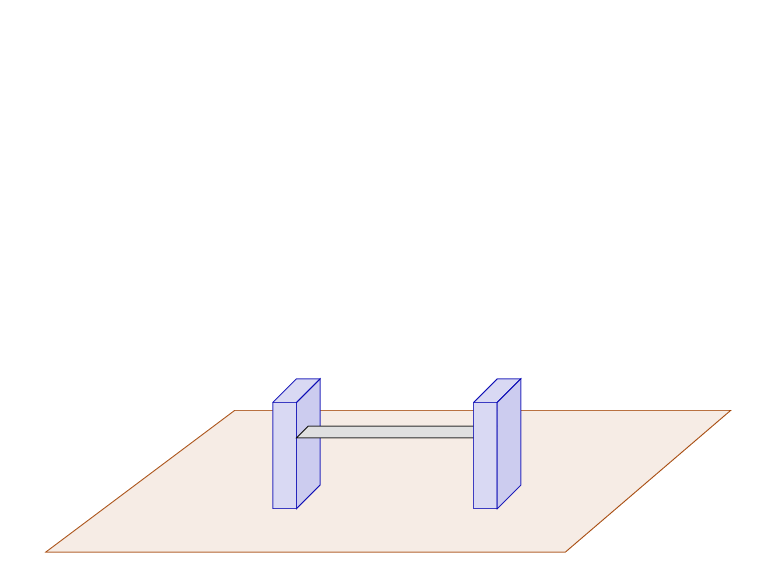
So, you place the first piece on the ground.

This first piece is solid and sturdy. It won't fall over. You can stand on this tiny ladder and be confident that you are safe. However, it's not high enough for you to reach the roof.
So, you get a second piece and stack it on top of the first. If you could place it PERFECTLY on the first one, with no error, then your new, taller, ladder would still be firm and safe.
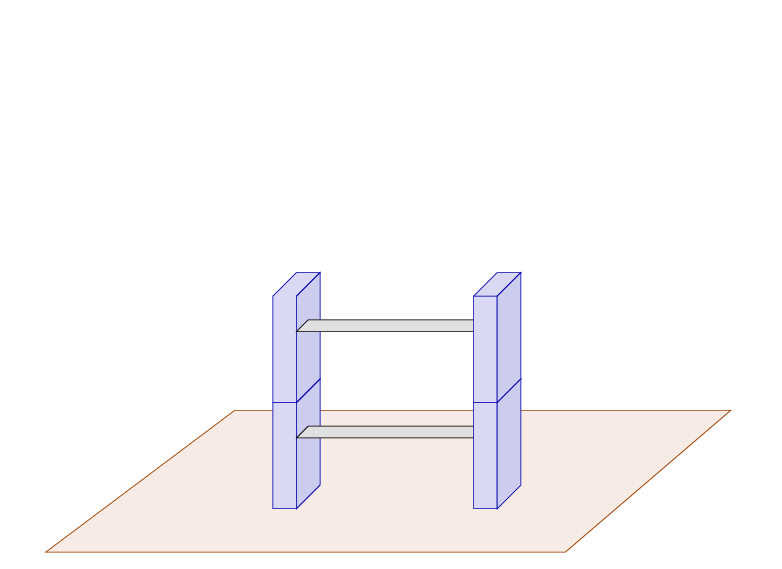
Unfortunately, when you place the second piece on top of the first, you can't avoid making a small error. It's not too bad, and the second piece is still quite strong.
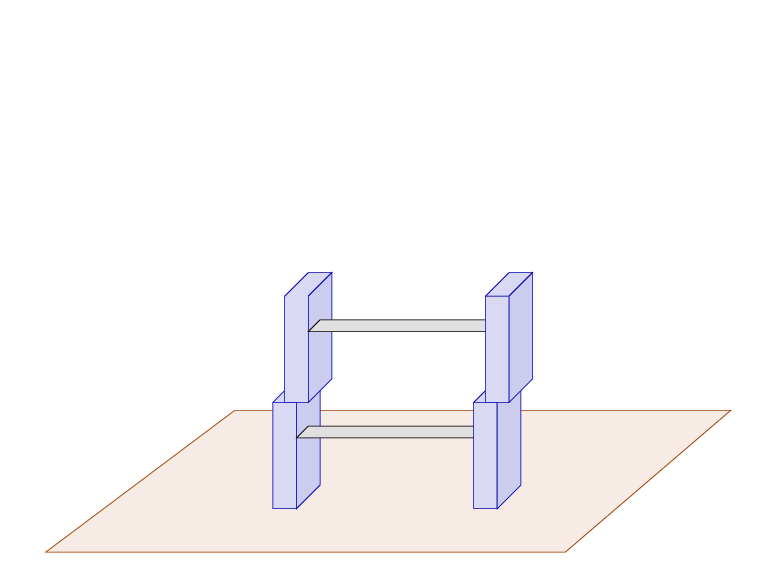
But -- it is still not tall enough for you to reach the roof of your house. So, you get a third piece. When you stack it on the second piece, you make another small error in a somewhat different direction.
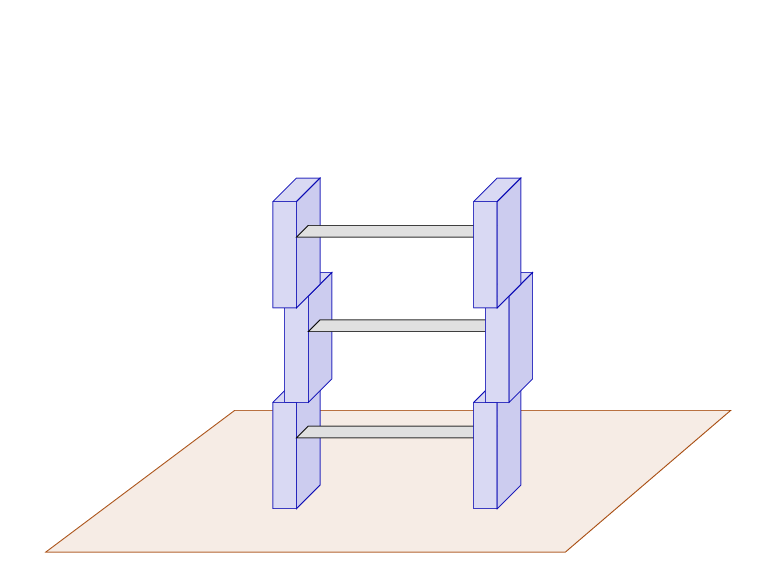
When you try to climb up onto the third step, you can feel the structure starting to shake a little.
But it's STILL not high enough!
So, you add a fourth section. There is no way to avoid it if you must reach the roof. But this step involves yet another error in the stacking.
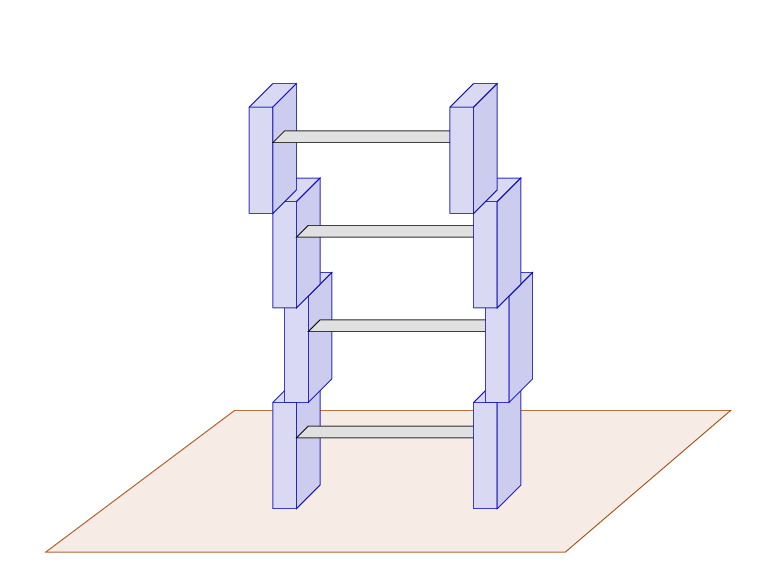
Now, at least, the ladder is tall enough to reach the roof of your house. But -- is it safe? Probably not. As you add more and more sections to the ladder, each one
and
By the time you CAN reach the roof, it's probably NOT SAFE to try.
Astronomers face a similar set of problems when they try to measure the distance to objects in the sky.
the ladder real astronomy
-------------------------------------------------------
first step close to ground close to Earth
very secure very well determined
second step sits on top of first step relies on smaller distances
has small instability has small uncertainty
third step sits on top of steps 1, 2 relies on previous measurements
more unstable has more uncertainty
fourth step sits on top of all steps relies on all other measurements
very unstable very large uncertainty
unsafe to stand unsafe to publish
-------------------------------------------------------
Of course, a ladder isn't the only structure which sits on firm foundations, but grows shaky as one moves to its upper reaches. The famous French astronomer Gerard de Vaucouleurs (who will appear later in this course) preferred to use the Eiffel Tower to illustrate this idea.
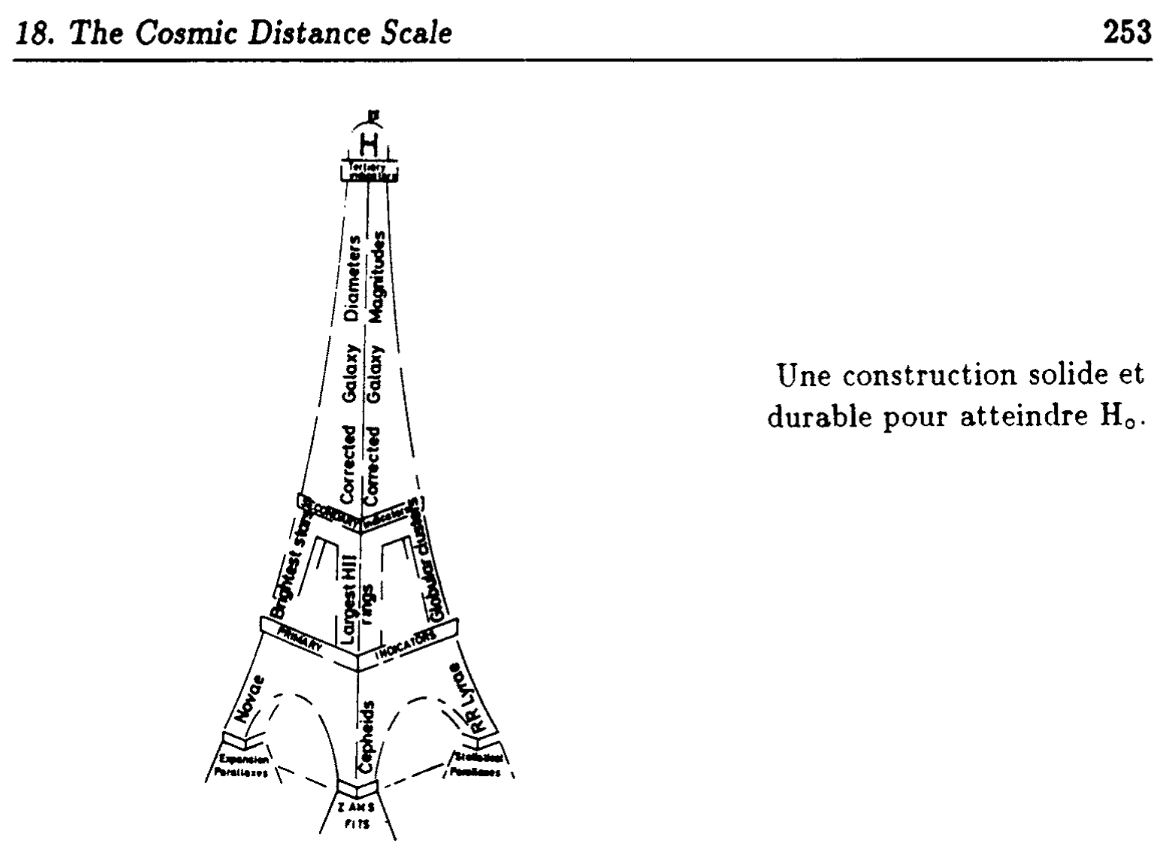
Figure probably created by de Vaucouleurs.
I haven't been able to track down the source of this image,
although one reference mentions the year 1976.
If you know the real source, please let me know!
A good way to gain a feeling for the manner in which results derived from a long sequence of operations can grow more and more uncertain is to perform such a sequence yourself. So, let's give it a try! Break up into groups, and prepare your calculators, pencils, and several sheets of paper.
The goal is to answer the following questions:
How many ordinary sheets of paper could be
transported on a single container ship?
What would the overall mass of those sheets be?
I will hand out to each group the following items:


Image of penny courtesy of
the US Mint .
Image of sheet of paper courtesy of
Shutterstock .
Your job is to answer the following questions. Write your answers neatly on the exercise worksheets, together with the names of everyone in your group.

Image of the Providence Bay courtesy of
Biberbaer
and
Wikimedia
When did astronomers start to use these terms? Searching through the literature for uses of these terms, I found the following candidates -- listed in inverse chronological order.
The distance estimate obtained in this manner does not depend upon a lengthy "cosmological ladder" ....
The establishment of a celestial reference frame and a cosmic distance ladder has been a major concern of astronomers throughout this century.
The modern "cosmic distance ladder" by means of which we estimate the distances of galaxies has been summarized by Weinberg (1971).
(MWR: this is a misprint in the original -- it should refer to Weinberg (1972), which is the book listed below)
(footnote 12) ... Changing mass will affect luminosities and thus "the cosmological ladder."
"The Cosmic Distance Ladder" is the title of section 14.5.
I can't find any instances earlier than 1972, which leads me to believe that Steven Weinberg may have coined the term. If you know of an earlier appearance, please let me know!
This course is too short to describe all the methods astronomers have adopted over the years to measure distances to celestial objects --- let alone to discuss each one in detail. I've chosen just a few of the methods which are perhaps most relevant to the current state of the field. We'll cover these topics in future lectures:
Traditionally, most parallax measurements have been made in the optical; with the launches of Hipparcos in 1989, and Gaia in 2013, that is certainly true. However, certain radio telescopes have also made contributions to this field, including Japan's VERA interferometer (see also one example of VERA's parallax work).
Examples of such special systems are
Some people might place the Baade-Wesselink technique of analyzing pulsing stars in this category, but I think that there are too many approximations for it to be listed in this group.
In a somewhat more dangerous manner, if we believe that we have accurate theoretical models of stellar evolution (which are properly calibrated), then we can compare the HR diagram of a real cluster to that of a simulated one and determine the absolute distance to the cluster. Warning: this can fail for many reasons ...
In the early days of observational cosmology, scientists such as Edwin Hubble and Allan Sandage chose individual stars for this method; that didn't work out very well, but at least it was a start. These days, astronomers rely on planetary nebulae and globular clusters, which can yield more reliable results.
One can even apply this method to the luminosities of entire galaxies within a cluster of galaxies, but the assumption that we understand the formation and evolution of galaxies well enough to compare them fairly across different clusters is (in my opinion) not a very good one.
Stars in elliptical galaxies do not all orbit in the same plane, or in the same direction; yet there appears to be a connection betweeen the motions of its stars and the luminosity of an elliptical galaxy. The connection is a bit more complicated in this case, going by the name of the fundamental plane.
These are both empirical relationships, although each has some theoretical explanation(s). Since we don't understand galaxies as well as we understand stars (in general), one should be careful not to apply these rules too far.
The bad news is that supernovae come in many varieties, some of which look very much like others. Even the generally well-behaved Type Ia events have a considerable number of outliers and oddballs. Perhaps worst of all, supernovae appear unpredictably and remain visible only for a few months, making it very difficult to find them and schedule enough follow-up observations to determine their properties accurately.
Supernovae are some of my favorite denizens of the sky, and I've been studying them since I was a grad student. I'll try not to let my enthusiasm take over when we discuss them; but if you'd like to talk about them outside of class, please visit my office!
In a few, very very rare instances, motions of bodies within the lensing object can lead to variations in the brightness of lensed images of a background source. In the best cases, the brightness of one image may change some days, or weeks, or months, before that of another image. If we can measure the positions of the background sources, the time delay between their variations, and properties of the lensing object, we can calculate the distances of the objects in a geometric manner.
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.