
Headline from Phys.org for Feb 25, 2023
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
You may have seen headlines like the following in newspapers or magazines or science-leaning website:

Headline from
Phys.org for Feb 25, 2023
What does this mean? What are "giant baby galaxies?" And why are they "impossible?"
Let's work our way through the real science behind these hyperbolic claims. There is a kernel of truth in them, but not much more than that.
As we've seen in the previous lecture, the universe is expanding on large scales. Our solar system isn't expanding, nor is our own Milky Way Galaxy; the gravitational (or electric) forces between objects in these "small-scale" systems are strong enough to prevent space from expanding. But on large scales -- distances between groups of galaxies, of order 10 or 20 Mpc -- space IS expanding, carrying galaxies along with it.
On large scales, there is a simple (initially) relationship between the distance d to a galaxy and its radial velocity v away from us:
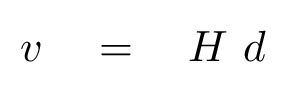
So, the farther away a galaxy is, the faster it recedes from us.
Of course, when an object moving away from us emits light, the wavelength of that light will be changed by the Doppler Effect. In the case of an object moving AWAY from us at speed v, the observed wavelength will be
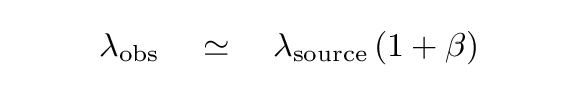
where β = v/c is a convenient shorthand. This equation becomes more complicated when the recession velocity approaches the speed of light:
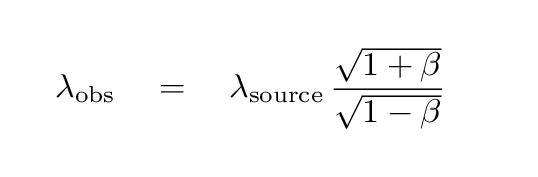
In either case, however, the bottom line is that light is REDSHIFTED so that the observer measures a longer wavelength. Astronomers are always comparing the observed wavelength of a spectral feature in their observations to the rest or source wavelength in order to measure these shifts. We use the following equation to quantify changes in wavelength due to radial motion; the quantity z is called redshift.
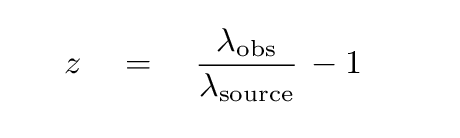
So, in short, galaxies which are very far away from the Milky Way will have large radial velocities -- which will create large redshifts in their spectra. We can turn this relationship around and use "large redshifts" to identify galaxies which must be very distant.
For ordinary stars in our own galaxy, moving at speeds much less than the speed of light -- just 10 to 50 or 100 km/sec -- these shifts are tiny: just a few Angstroms at most. Will that cause any appreciable change in the COLOR of the star?
Well, let's find out. Consider a star like Vega: a little hotter than the Sun, but nothing special. Most of its light appears in the optical part of the spectrum, with a small amount in the UV ...
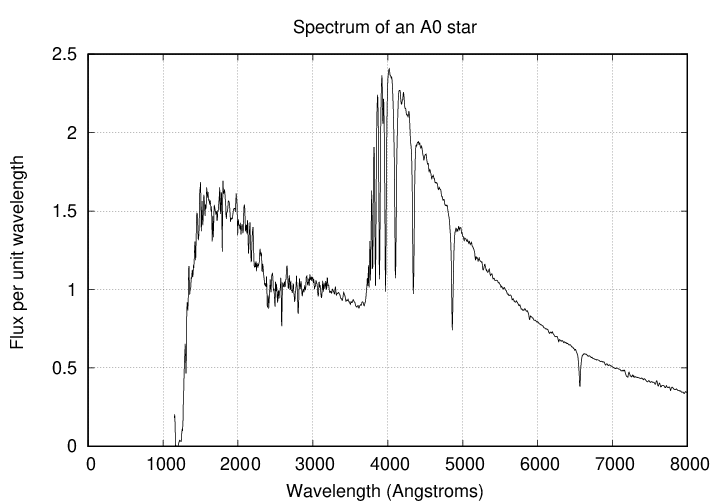
.. and very little light in the infrared.
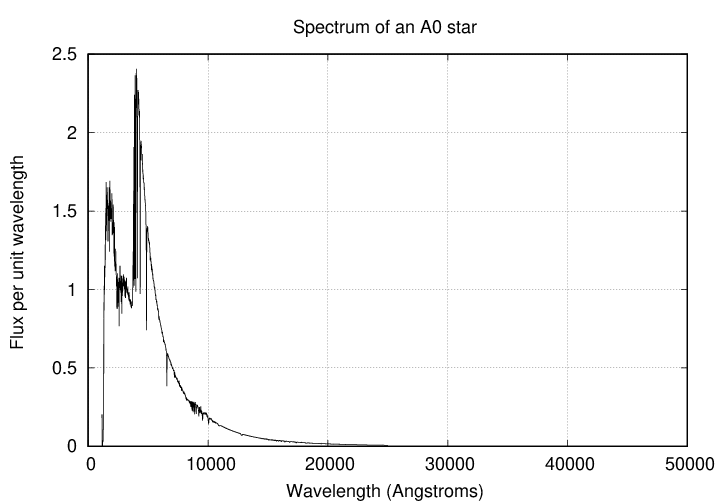
A simple way to express the color of a star like this is to measure its magnitude through a pair of filters, such as B and V, and then subtract one magnitude from the other.
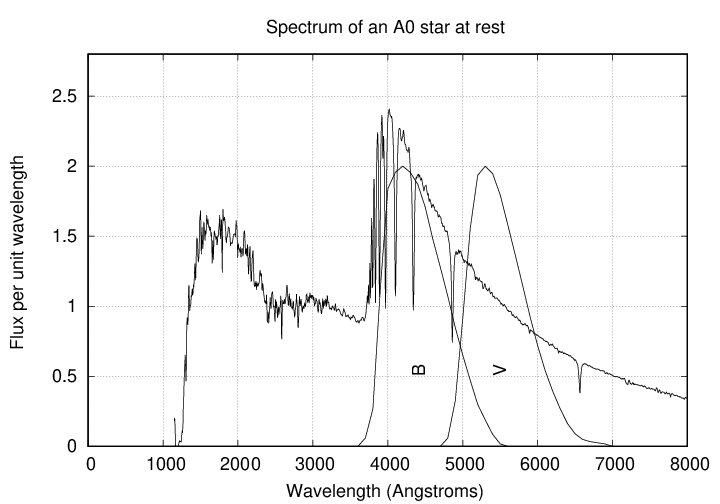
Q: Will the (B-V) color be a large positive number,
or a smaller number -- maybe even negative?
Yes, that's right: hot stars like Vega have (B-V) values which are small, close to zero, or even negative. They are hot and blue-ish.
Suppose that a star like this happens to be moving away from us. Its light will be shifted to longer wavelengths -- but will its properties change by a significant amount? A very few stars in our Milky Way are moving with speeds approaching 1,000 km/sec; we think they suffered a close encounter with a massive compact object, and the strong gravitational forces at that time gave them a violent "kick". Even these "hypervelocity stars" have redshifts which are much smaller than z = 0.01, but let's use that value as an upper-upper limit to the motion of ordinary stars.
What would such a redshift do to the measured (B-V) color of a star?
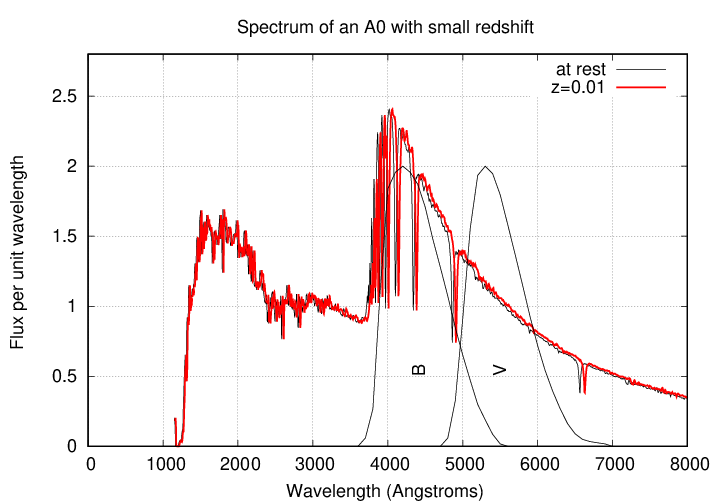
Q: How much would the (B-V) color of a star change if it
had a redshift of z = 0.01?
Answer: not much at all, even at this ridiculous velocity.
Now, suppose that a star happens to be located very, very far away from the Milky Way, so far away that the expansion of the universe is carrying it away from us at an extremely high speed v; so fast, in fact, that the light from the star is redshifted to z = 7.
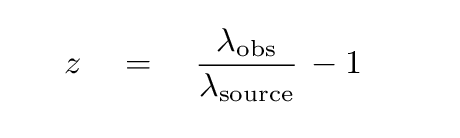
Q: At rest, the star's spectrum has a peak around
λsource = 4200 Angstroms. What is the observed wavelength at z=7?
That's right: now, the peak appears in the near-infrared, around 32,000 Angstroms = 3.2 microns.
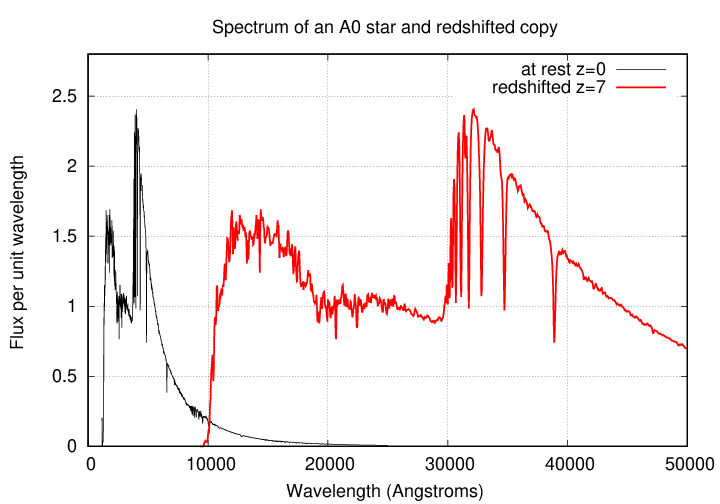
At this redshift, none of the star's light appears in the visible region of the spectrum at all! If we looked with an ordinary optical telescope, we'd see nothing.
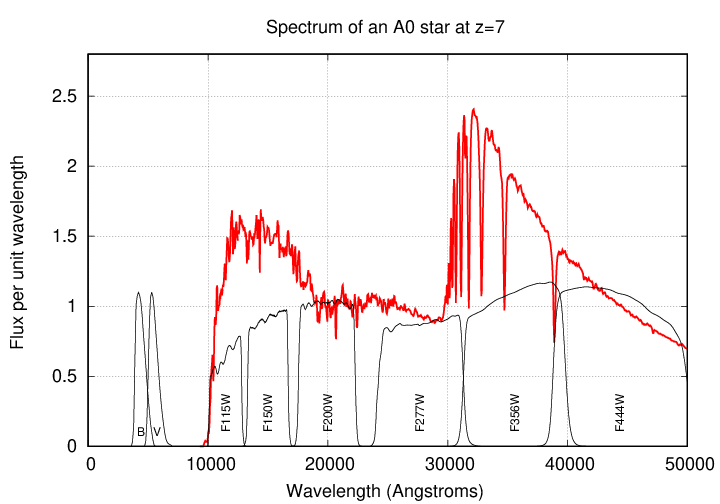
On the other hand, if we observed this star with an infrared telescope, we'd see a small amount of light through filters between 11,000 and 27,000 Angstroms (labelled as F115W through F277W below)

Closeup from Figure 2 of
Labbe, I., et al., Nature 22 Feb 2023
and a jump in apparent brightness in filters around 30,000 and 40,000 Angstroms (labelled as F356W through F444W below):

Closeup from Figure 2 of
Labbe, I., et al., Nature 22 Feb 2023
Ordinary stars and galaxies at rest do not emit light with a spectrum like this. If we see an object which is invisible in the optical, but produces a small amount of near-infrared light and then shows a big jump in the mid-infrared, we might conclude that we are looking at a collection of ordinary stars at high redshift -- which means a galaxy which is very distant.
In the last few decades, some astronomers have used the shift in colors caused by the very large recession velocities to search efficiently for very distant galaxies. The basic idea is pretty simple: take deep pictures of some region of the sky with a set of filters which cover a wide range of wavelengths, from the optical to the mid-infrared. Measure the brightness of each object through each filter. Look for objects which show a pattern like this:
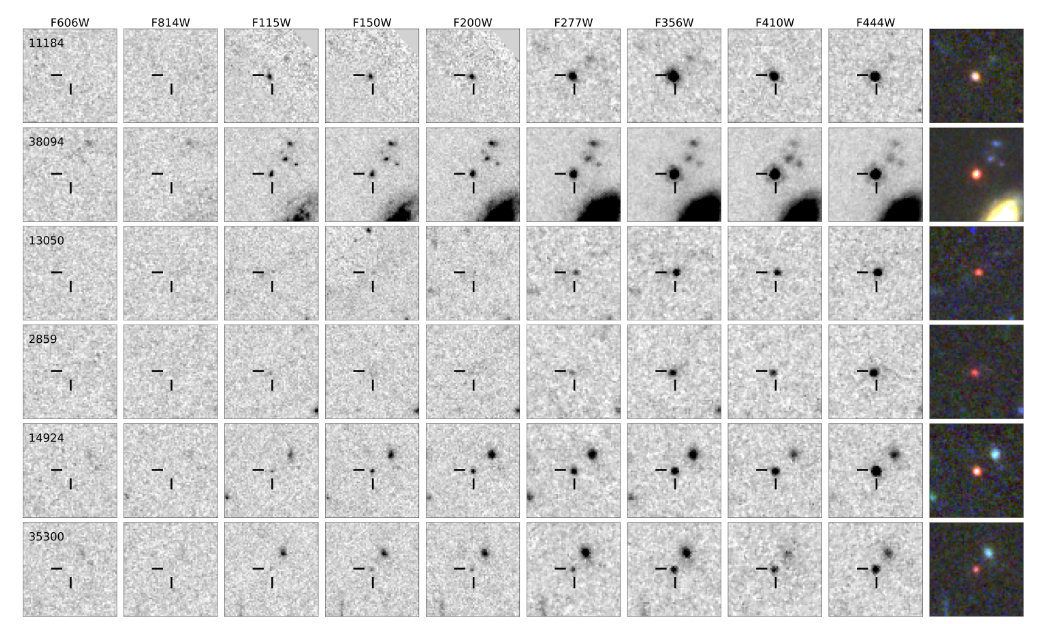
Figure 2 of
Labbe, I., et al., Nature 22 Feb 2023
One of many such searches is described in Labbe, I., et al., Nature 616, 266 (2023). The group used some of the early images acquired by JWST to look for objects with these unusual colors which might indicate a high redshift and great distance. The figure below shows a few of their candidates.

Figure taken from Labbe's press release on
Phys.org for Feb 25, 2023
Notice that all these candidates appear as small, red dots.
Light rays travel fast: c = 3 x 108 m/s. On Earth, in our ordinary lives, that means no appreciable delay between some event -- say, a firework's explosion on July 4 -- and our perception of the event.
But when light rays have to travel interstellar distances, even they take quite a bit of time to make the journey. Light from our nearest neighbor, the Alpha Centauri system, takes roughly 4 years to reach the Earth. That means that when we see Alpha Cen in our telescopes, we are actually observing it as it was 4 years ago.
Galaxies are much farther away, of course, and so we see them as they were much farther into the past.
Q: The Andromeda Galaxy, M31, is roughly 750 kpc from the Earth.
What is the "lookback time" to this galaxy?
For relatively nearby galaxies, we can compute their "lookback time" in a simple manner:
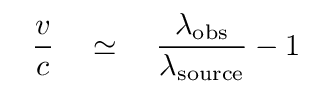
D = (velocity) * H0
Let's do a simple little example.
Q: The galaxy M87 has a radial velocity of v = 1280 km/s
away from the solar system.
Estimate the time it takes for light to travel from M87 to Earth.
However, when the recession velocity is large enough to approach the speed of light, our simple approximations for the redshift stop working. Even more important, on these large distance scales, the geometry of the universe itself begins to deviate from a simple "flat" Euclidean space. When this happens, the simple relationships between velocity and redshift and distance break down ... and therefore the simple relationship between redshift and light-travel time also breaks down.
Is there any way to find the light-travel time for a high-redshift galaxy, without doing a lot of really gnarly math? Yes, thank goodness. A number of kind scientists have created "cosmology calculators," which will perform all the complex calculations at the touch of a button. I like to use Ned Wright's Cosmology Calculator.

Ned Wright's Cosmology Calculator
Give it a try! Using the default parameters and the "General" model,
Q: What is the light-travel time for a galaxy at redshift z = 1? Q: What is the light-travel time for a galaxy at redshift z = 8?
The last step we need to carry out is a simple one. If we measure the redshift z of an object, can we figure out how long AFTER THE BIG BANG it must have emitted the light which are currently observing? In other words, can we figure out the AGE of an object based on its redshift?
For example, our best current estimates of the age of the universe is about 13.8 billion years. If it takes light 5 billion years to travel from some galaxy to us, then the light from we now measure must have left the galaxy about (13.8 billion - 5 billion = 8.8 billion) years after the Big Bang. If that galaxy formed immediately after the Big Bang, then it would be 8.8 billion years old when it emitted that light.
So, if we determine that some particular galaxy has redshift z, we can
Okay, we're almost ready to address those headlines mentioned at the start of today's lecture. Our current model of the universe -- which we will discuss in detail later -- postulates a beginning, the Big Bang, roughly 13.7 billion years ago. We think that at that time, all the material in the universe was a soup of very hot gases, almost entirely hydrogen and helium. There were no stars and no galaxies at that time -- just hot gas.
Over time, the gas cooled off, and some clouds of gas collapsed to form dense clumps which became stars. In some regions of space, gigantic collections of clouds became collections of stars, which eventually turned into galaxies. Astronomers are currently struggling to answer a number of questions associated with these processes in the early universe.
I think that the current idea is that the first galaxies were rather small compared to the Milky Way, or other big, pretty galaxies in our current corner of the universe. Over time, some of the initial mini-galaxies merged and collided and eventually turned into bigger objects. But I'm definitely NOT an expert in this area.
As a rough estimate, suppose that models of structure formation after the Big Bang suggest that galaxies of the size and mass found in these JWST images ought to take 1 billion years to form.
In the figure below are some of the high-redshift galaxies identified by Labbe, I., et al., Nature 22 Feb 2023 in their JWST images.
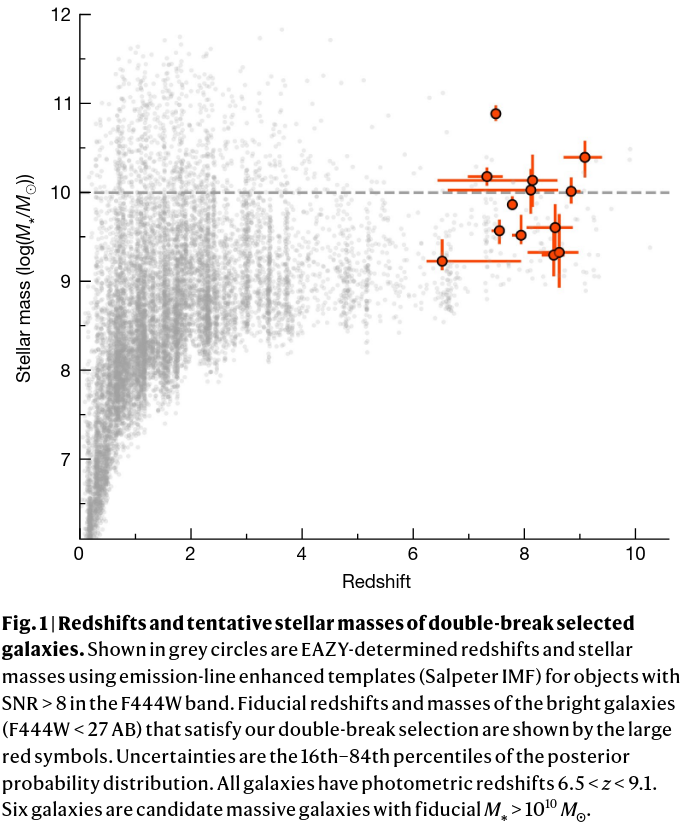
Figure 1 taken from
Labbe, I., et al., Nature 22 Feb 2023
Q: What is the maximum redshift in this set of objects?
Q: What is the light-travel time for a galaxy at that redshift?
Q: If the universe is 13.8 billion years old, what is the maximum
possible age for a galaxy at that redshift?
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.