
Table 1 taken from Ferriere, K. M., Reviews of Modern Physics, 73, 1031 (2001)
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
The space between the stars in the Milky Way may look empty in some ways, but it's actually a complex stew with many different ingredients. The table below shows a very rough breakdown of the various types of gaseous and particulate matter can collect into larger, recognizable units. We will go over some (but not all) of these structures in detail over the next few weeks.

Table 1 taken from
Ferriere, K. M., Reviews of Modern Physics, 73, 1031 (2001)
The categories in the table above have labels which describe the physical properties of the different phases of the ISM using words -- good ol' words that make sense. For example, "molecular" gas is composed mostly of molecules. Sensible, right?
Astronomers, of course, have devised a set of labels of their own which are more compact, but which can be confusing to those new to the field. Here are some synonyms for the entries in the table. Please do try to memorize these, as both I and the literature quoted in these lectures will be using them frequenty.
Some clouds of this cold, dense, material are very large, up to tens or hundreds of parsecs in size. For that reason, these large collections are sometimes called giant molecular clouds or "GMC" for short.
So, for example, "HI" means "hydrogen, from which zero electrons have been removed" or "neutral hydrogen". The label "OIII" means "oxygen atoms from which two electrons have been removed."
But the most common variety of this phase are clouds of hydrogen (and small amounts of other elements) close to hot, young stars. The high-energy radiation from those stars strips most of the electrons away from their atoms, leaving a soup of electrons and protons. Since singly-ionized hydrogen is the most common ingredient in such clouds, they are usually referred to as HII regions. The pronunciation of this phrase is "aitch two regions".
Do you recall the Ideal Gas Law from chemistry and physics classes? In a number of common situations, there is a simple relationship between the pressure, temperature, and density of a gas:
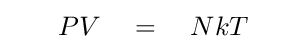
Here,
One can divide both sides by the volume to find another way to express the gas law.
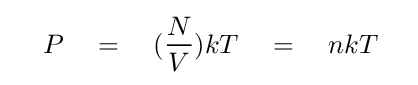
In this version, the pressure depends on just two quantities on the right-hand side: density and temperature. Look again at the table of typical values for interstellar material:

Table 1 taken from
Ferriere, K. M., Reviews of Modern Physics, 73, 1031 (2001)
Q: What is the pressure of each of these phases?
Multiply the density (in cm-3) by the temperature (Kelvin)
and just pay attention to the magnitude of the result.
You should find that all the combinations of density and temperature yield a pressure which is roughly the same, to within an order of magnitude. In other words, the various phases of the ISM appear to be in rough pressure equilibrium.
Of course, these values are simply representative ones; real clouds vary in their properties. Still, the near-equality of these pressure values means that, on average, clouds of one type are not usually compressing those of another type, or expanding into their space, at least on the largest scales.
As gas particles -- ions, atoms, molecules -- fly through space, they will occasionally bump into each other. Collisions can cause significant physical changes to the material, so it's important to be able to figure out
The first of these is called the mean free path, or "mfp" for short. Let's find a way to calculate an approximate value.
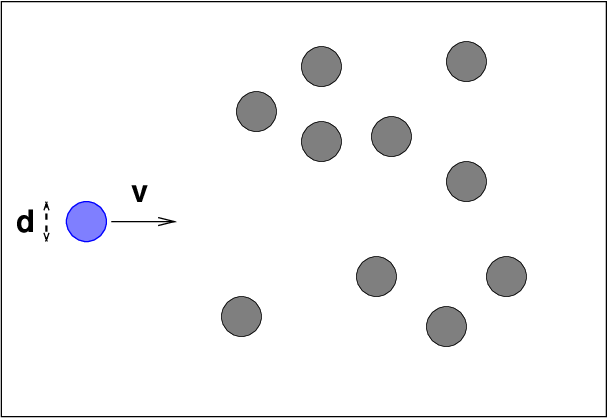
If we have a gas of atoms with typical diameter d and radius r = d/2, with density n atoms per unit volume, the question is -- how far will the blue particle typically travel before it strikes an atom? We can simplify the calculations by imagining an equivalent situation, in which the blue particle becomes twice as big and all the other particles shrink down to perfect little points:
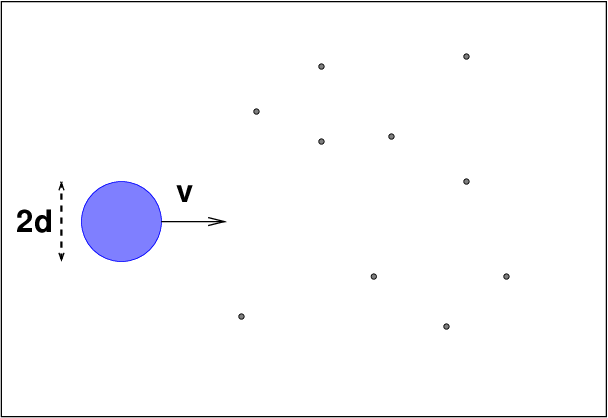
Collisions between the blue particle and others will occur just as frequently now as in real life, but we don't have to worry about the mathematics of intersecting circles anymore.
Now, as the blue particle moves through the sea of other particles, it will sweep out a cylindrical path ...
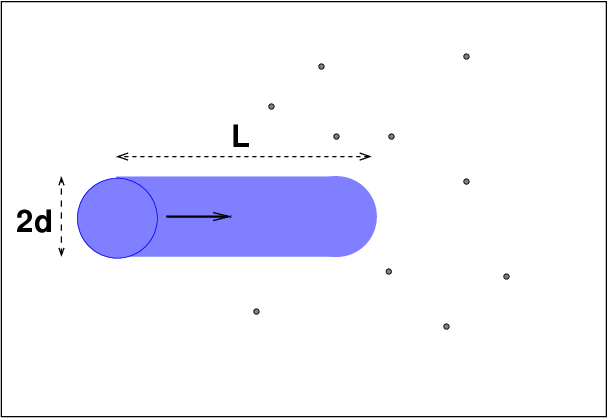
Q: What is the volume of this cylindrical path?
The mean free path is the average distance the blue particle must move until another particle falls within the volume it sweeps out. That's just another way of describing the distance between collisions.
We can compute the mean free path by setting the volume swept out by the blue particle to the typical volume occupied by each particle in the gas. In other words, if each particle typically has a volume V to itself, then when the cylinder grows to have volume V, it will typically contain at least one other particle.
Suppose the density of the gas is n particles per cubic meter. Q: What is the typical volume per particle? Q: Write an expression for the mean free path L.
There is quite a wide range of conditions in gas clouds in the Milky Way, but the values listed back in the overview are pretty typical for HI clouds.
density n ~ 25 atoms per cubic cm = 25,000,000 per cubic meter
diameter d ~ 1 Angstrom = 10-10 meters
Q: What is the mean free path of a hydrogen atom in an HI cloud?
That's ... quite a distance between collisions. Is there a chance that each atom simply flies off into space and leaves the cloud, causing it to evaporate?
Yes, there is a chance -- but it turns out to be small one. Even the tinest HI clouds are much, much larger than the mean free path; for example, the clouds described by Stanimirovic, Heiles and Kanekar (2007) are between 800 and 4000 AU in diameter. If the mean free path of atoms is about 2 AU, then only a miniscule fraction of atoms at the outermost skin of a cloud has a chance to escape into space.
Now that we know the mean free path -- the DISTANCE between collisions -- we can estimate the TIME between the collisions. After all, the distance L is simply the product of a particle's speed and the time between collisions. So, if we know the typical speed of a hydrogen atom in space, we can figure out that time.
The speed of gas particles depends on the temperature of the gas in the following way,
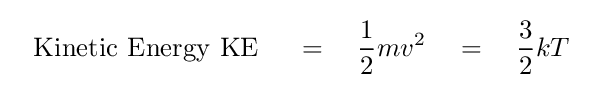
where
One can then derive
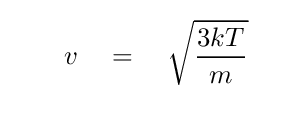
Temperatures in clouds of neutral hydrogen vary quite a bit, depending on the local environment, but a typical value is around T ~ 50 K.
Q: What is the speed of hydrogen atoms in a cloud of HI?
Q: What is the typical time between collisions?
Express your answer in seconds and years.
You may recall that the time required for an isolated hydrogen atom in the excited hyperfine state to de-excite and emit a 21-cm photon was around 10 million years(!). In a typical HI cloud, many of these atoms will bump into others long before that critical time, often moving the atom into a different energy state. Apparently, only a very small fraction of the neutral hydrogen atoms will survive long enough to emit 21-cm radiation -- but that tiny fraction is enough for our radio telescopes to detect and measure.
We discussed previously how the strong 21-cm emission of neutral hydrogen gas can be used to map out the structure of the Milky Way's disk. That radiation can also be used to estimate the amount of gas in HI clouds. How does the mass of the gas in the ISM compare to the mass in the form of stars?
It's not too hard to calculate a rough estimate of the mass of gas. The graph below shows the "surface density" of both neutral hydrogen (HI) and molecular hydrogen (H2) in the plane of our Galaxy, as a function of distance away from the center. What does "surface density" mean in this context?
The amount of material within this region is equivalent to the surface density of gas in the disk of the Milky Way, in units of solar masses per square parsec.
So, for example, if we wished to calculate the mass of all the interstellar gas within the rectangular box in the figure below, we would first compute the area of the box: (L x W) square parsecs. Next, we'd multiply by the surface density of gas, (solar masses per square parsec), to end up with the mass of the gas within the region.

Image of M101 courtesy of
Subaru Telescope (NAOJ), Hubble Space Telescope;
Processing & Copyright: Robert Gendler
The surface density values shown below are based on measurements made by radio telescopes at several observatories. The dotted black and solid blue lines show the surface densities of HI gas determined by telescopes looking at the northern and southern galactic hemispheres, respectively.
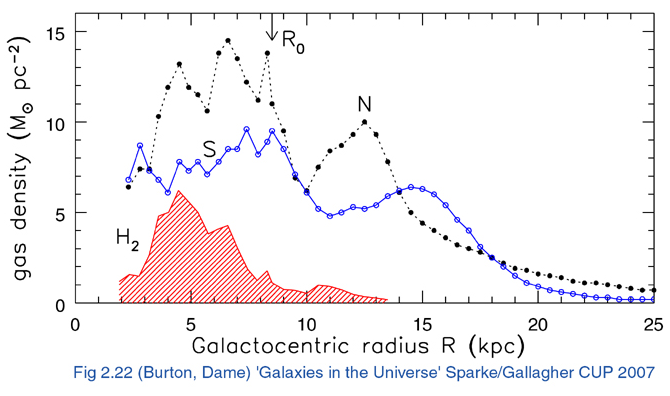
Figure 2.22 taken from
Galaxies in the Universe: an Introduction
by L. S. Sparke and J. S. Gallagher, III (2007).
This figure based on data provided by W. Burton and T. Dame.
Q: What is the average value of the surface density of HI
between radii of 2 and 20 kiloparsecs?
Q: Compute the area of a circular disk of radius 20 kpc.
Q: What is the total mass of the HI gas within 20 kpc
of the galactic center?
For comparison, the mass in the form of stars within the same region is roughly 5 - 10 x 1010 solar masses. It's clear that gas makes up only a minor component of the Milky Way's mass, at least in these inner portions of the Galaxy.
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.