Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
We now have ways to measure several properties of stars:
But what good does it do? We can make up tables containing hundreds or thousands of stars, with columns for apparent magnitude, temperature, etc. -- okay. It would help, though, if we could discover just a few simple relationships between these variables; humans are very good at remembering and pondering a few, simple rules, but very bad at remembering thousands and thousands of numbers.
Are there any simple relationships hidden in this wealth of data? The answer, of course (why else would I ask the question?) is YES. Let's set the Wayback Machine for the early 1900s, when astronomers first compiled the raw numbers for hundreds of stars ....
One of the astronomers who gathered together in one place measurements of many stars was the Danish scientist Ejnar Hertzsprung. He wrote several papers in which he identified correlations between different variables. However, since he presented his work in tabular form, it wasn't easy to grasp the signficance of any particular relationship. Moreover, he published in rather obscure journals. As a result, when his work was first published around 1905, it did not make big waves.
Several years later, another astronomer dug into the data independently. Henry Norris Russell was a famous scientist at a prestigious institution, Princeton University, so people tended to pay attention to his work. Moreover, he singled out one particular relationship between stellar properties and presented it in a graphical form. In 1913, he described his findings at a meeting of the Royal Astronomical Society.
His discussion centered on a diagram which showed the absolute magnitude and spectral class of stars. The very first versions had absolute magnitude on the horizontal axis and spectral class on the vertical axis, but within a year, he switched to the format which has been universally adopted:
This figure appears in Russell, Nature, 93, 252 (1914)
Long after Russell's graph first appeared, another astronomer pointed out that the same relationship had appeared previously in Hertzsprung's work. We now recognize the achievements of both astronomers by referring to it as the Hertzsprung-Russell diagram, or "HR diagram" for short.
You may be saying to yourself, "Well, um, okay, so Russell made a diagram. What's the big deal?" Let's go over the diagram slowly.
There are several different ways to label the axes, and you may see different combinations in different places. Let's start with the vertical axis: in Russell's original, it shows absolute magnitude. But we can replace this with any measure of the true power output of the star. The usual possibilities are
Q: Where are the powerful stars in this diagram? Q: Where are the feeble stars in this diagram?
Right. Powerful at top, feeble at bottom.
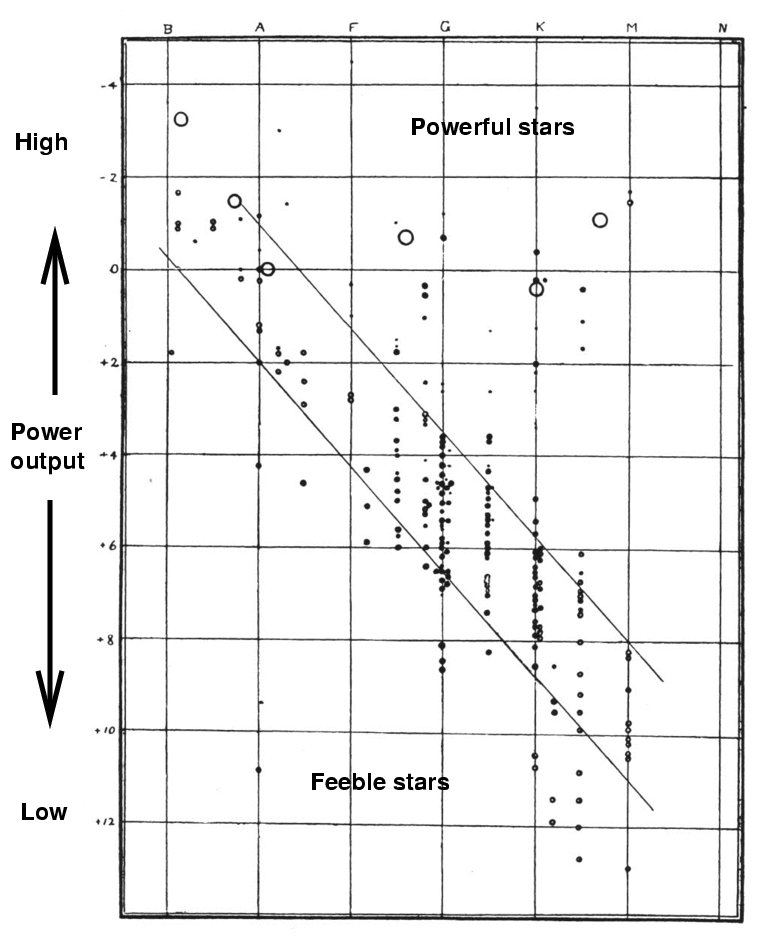
Q: The Sun has (roughly) absolute magnitude V = 5.
Where does it fall in this diagram?
How many solar luminosities do stars at
the top of the diagram produce?
How many solar luminosities do stars at
the bottom of the diagram produce?
The horizontal axis is, in the original, labelled "spectral class". But that's not the only quantity which one can find on this axis: there are two other quantities which are roughly equivalent, and which frequently appear in its place. You may see any of these three variables on the horizontal axis:
So, for example, if we use color index, the graph would look like this:
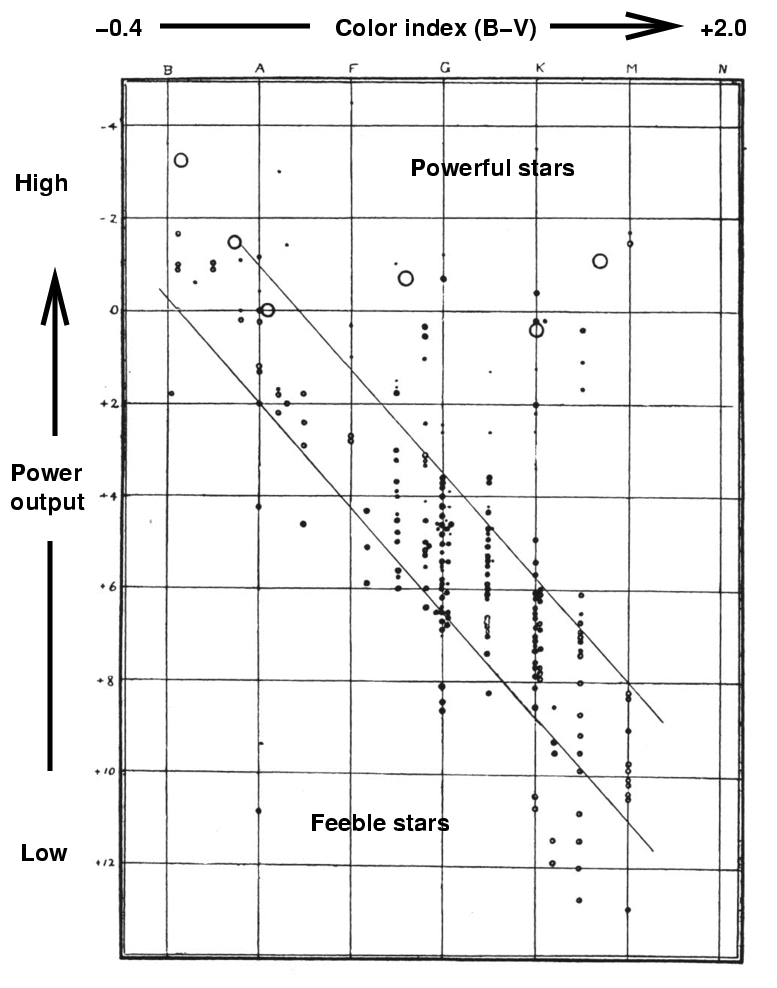
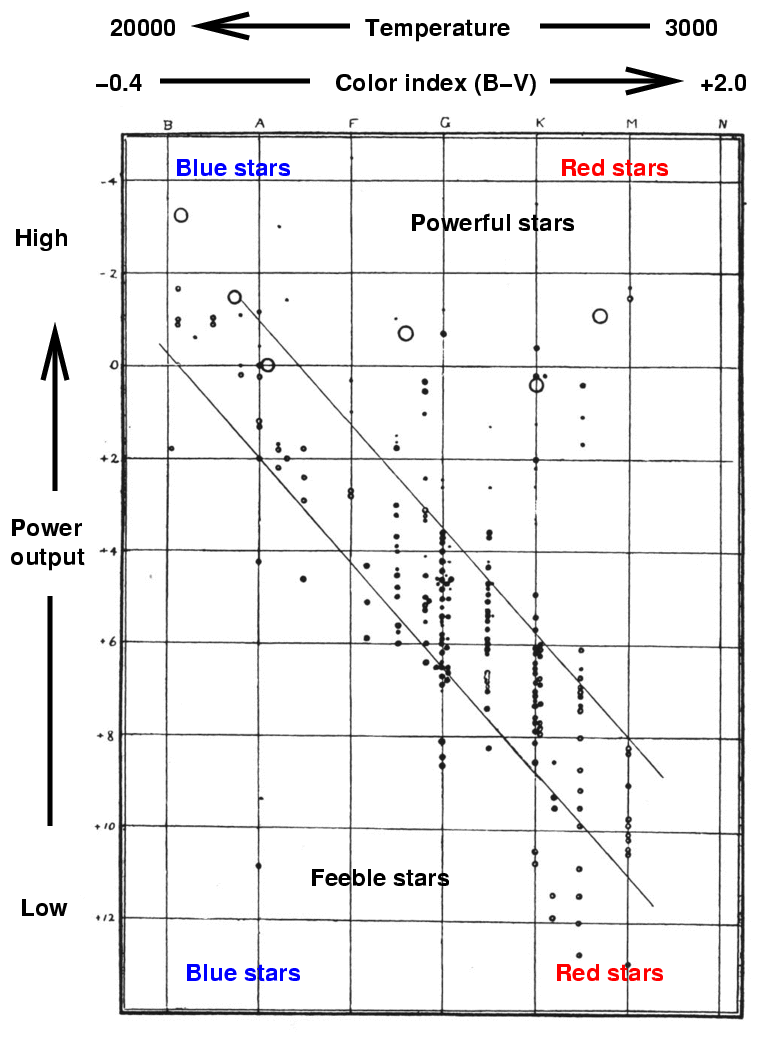
Q: Where are the hot stars in this diagram? Q: Where are the cool stars in this diagram? Q: Where are the blue stars in this diagram? Q: Where are the red stars in this diagram?
Right. Hot, blue stars on the left, cool, red stars on the right. Note that temperature runs backwards on this diagram.
Now, Russell noticed that the great majority of the stars in the catalogs of his time fell in a band which ran from the upper left to the lower right. He indicated this in his version of the diagram with lines; we now call this region the main sequence.
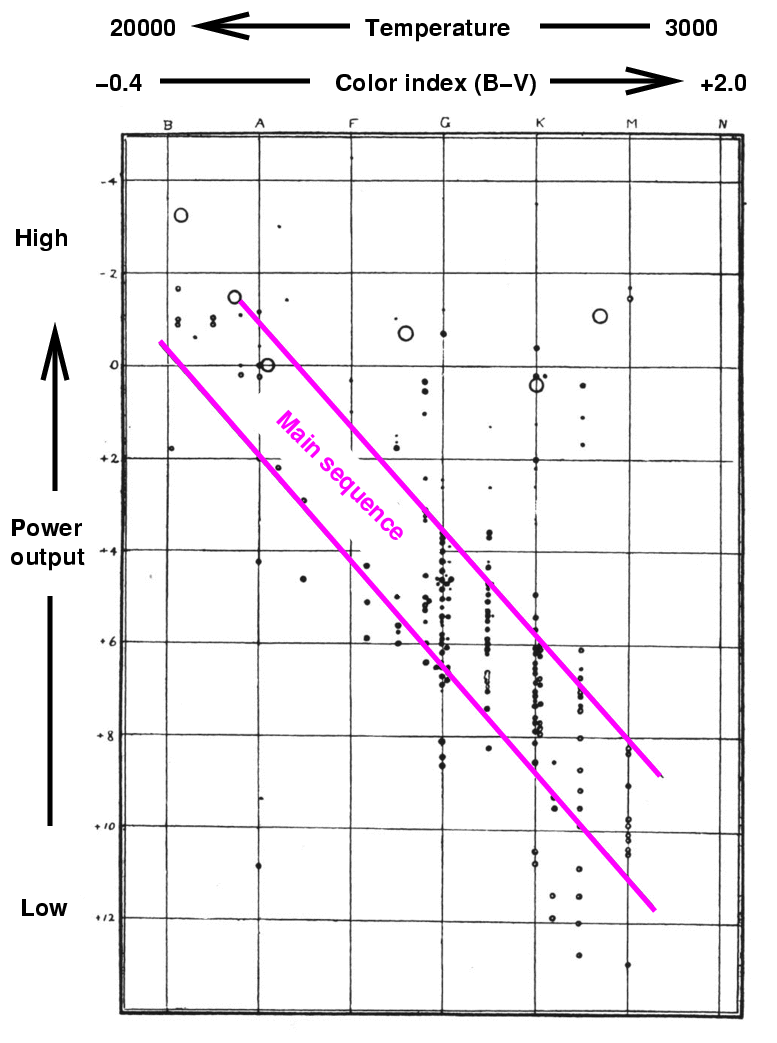
He also noticed the difference in the other two corners of the diagram: there were some stars in the upper right, but very very few stars in the lower left. Hmmmm. What could this mean?
Well, think for a moment about these corners. Stars in the upper right region are powerful and cool.
Q: How does the temperature of a star
affect the power it emits from each
square meter of its photosphere?
Q: So what does this imply about stars
which are both powerful and cool?
Right. These stars must be very large -- they must have a very big surface area in order to produce so much power with at such low temperatures. Hertzsprung gave the name giant to the stars with this combination of features, and we have kept it ever since. You often see the term red giant, since most of the stars are reddish. Note that this important feature of the stellar population -- that cool stars come in two sizes -- is a simple consequence of the gap between the bright and faint groups on the right-hand side of this diagram.
Both Hertzsprung and Russell noticed this gap between the luminous and feeble red stars, and decided to give names to the two groups. If the powerful red stars are called "giants", then the feeble red stars should be called .... "dwarfs."
And so they were (and are).
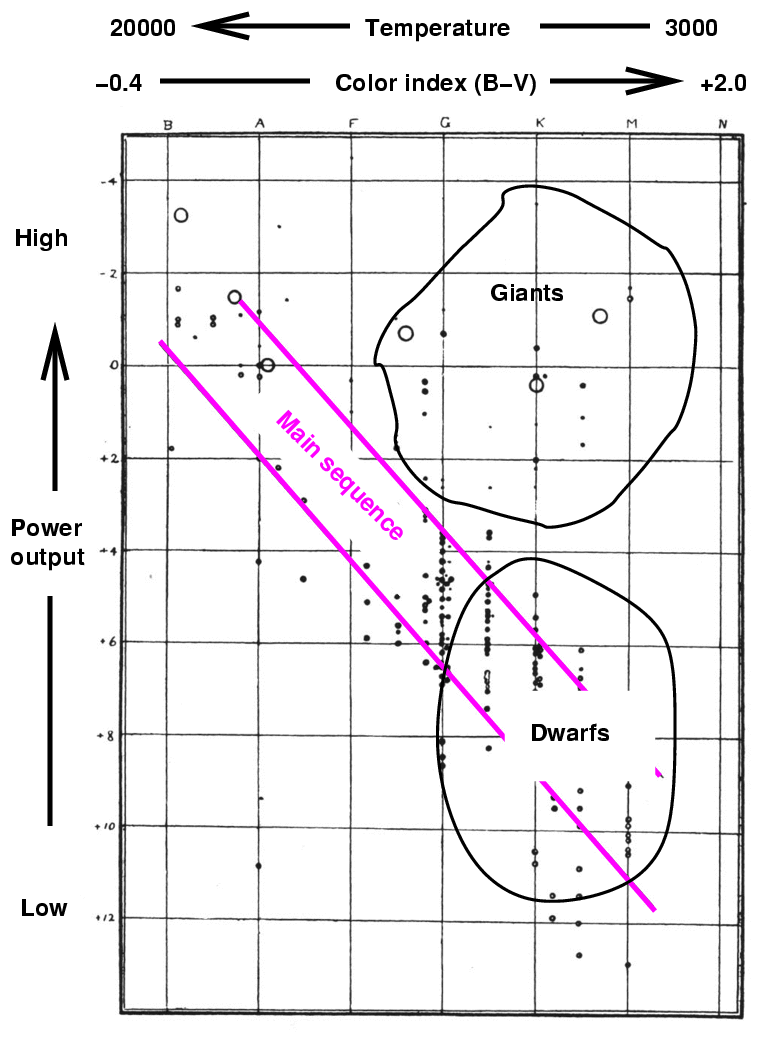
However, Russell realized that these "red dwarfs" were really just the cool end of the main sequence of stars. As a result, he decided to extend the term dwarf to refer to ANY member of the main sequence, not just the red end.
So, you may sometimes see these labels on stars:
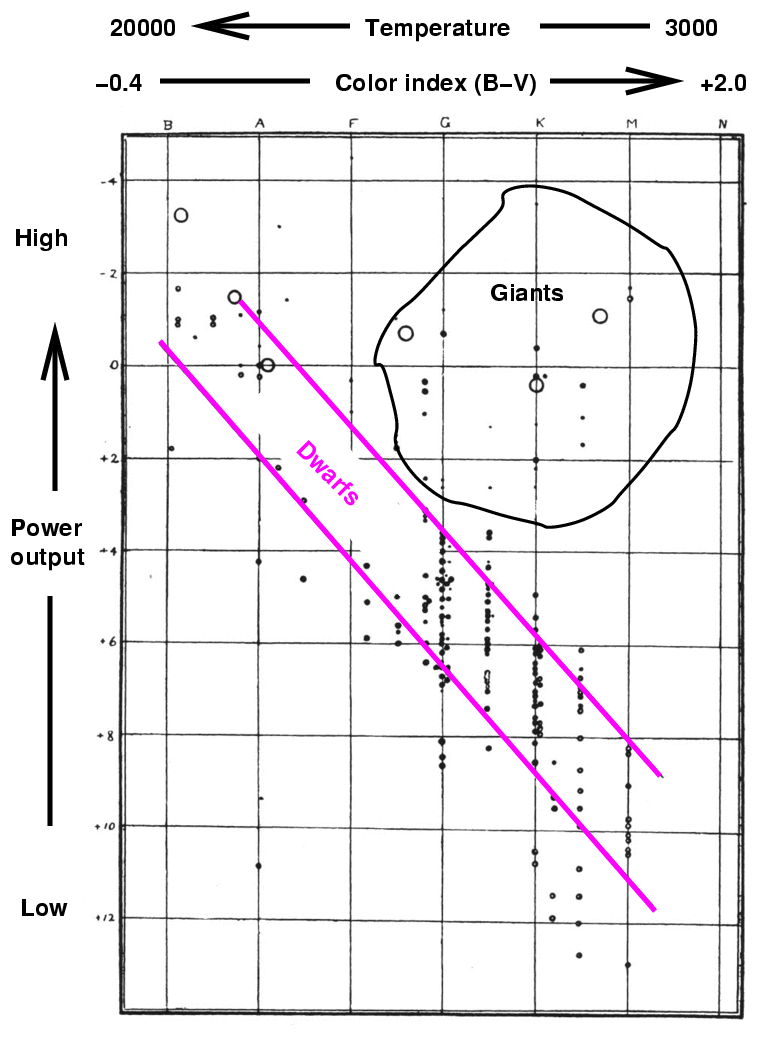
At the time Hertzsprung and Russell created this diagram, they knew of very few stars which fell in its lower left corner: stars which were hot, yet feeble.
Q: What sort of star could be very hot,
yet produce little power?
Right. The only stars which could fall in this region of the HR diagram would be very small stars. And when I write, "very small", I mean "much, much, MUCH smaller than ordinary stars." Just how small would they have to be? Look at Russell's diagram: there is one dot at
Q: What is the luminosity of this star?
Express your answer in Watts, and in terms
of the solar luminosity (3.8 x 1026 Watts).
Now, if this star emits radiation like a blackbody, then its luminosity depends simply on its radius R, temperature T, and the Stefan-Boltzmann constant σ = 5.67 x 10-8 Watts per sq.m. per K4.
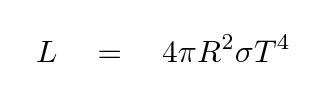
If we know the luminosity and temperature and want to find the radius, we can turn this equation around:
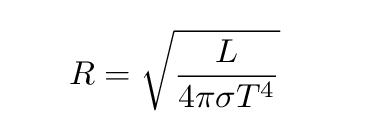
Q: Assuming this star emits like a blackbody,
figure out its radius in meters.
Then compare it to the size of the Sun
(which has radius roughly 700,000 km).
Because stars in this region of the diagram are so small, astronomers could not help themselves: they use the term "dwarfs" to refer to these tiny hot stars, even though they do not fall on the main sequence, and even though they are an order of magnitude smaller than the "red dwarfs" at the lower end of the main sequence. Since these stars are hot, though, they receive the name white dwarfs.
If one looks again at Russell's diagram from 1914, one can see at a glance that the number of stars is not very large: perhaps two hundred. Some regions of the diagram are very sparsely sampled, and the large-scale patterns one can see are limited to the main sequence and a very ill-defined giant branch. The fact that both Hertzsprung and Russell were able to recognize these groups is a credit to their understanding of the data.
Fortunately for us, advances in technology have created much larger samples of stars with well-measured properties. The Gaia mission's Data Release 2, for example, contains entries for over one billion stars, many with very high precision. Let's use it to create our own HR diagrams.
First, let's do what Hertzsprung and Russell did: pick the brightest stars in the sky -- which were the only stars for which most properties could be measured back in the day -- and plot absolute magnitude versus color. In this case, we'll use the Gaia version of color: (GBP - GRP), or, for short, (B-R). So, we'll search for all apparently bright stars, with apparent magnitude < 10, which also have well-measured distances. "Well-measured" will mean "the uncertainty in parallax angle is less than 10 percent", which is a reasonable way to avoid bogus results.
If one visits the Gaia Archive site , one can perform this search using the following special language:
SELECT * FROM gaiadr2.gaia_source WHERE phot_g_mean_mag <= 10 AND parallax_over_error >= 10
The HR diagram of these stars (actually, a subset, just 50,000 of the full set of 451,000) looks like this:
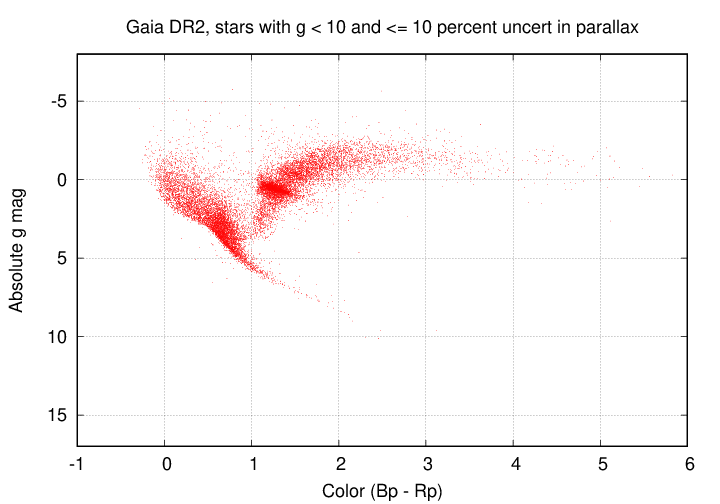
Q: How does this diagram compare to the 1914 version? Q: What is the ratio of giants to main-sequence stars? Q: Do you see any structure within the red giant region?
The diagram above includes stars both nearby and very distant. The distant ones, of course, much be very luminous in order to appear bright in our skies; in other words, they must be giants. That accounts for the large number of stars in the giant region. In fact, the fact that we are picking only stars which appear bright creates a selection bias, favoring the inclusion of powerful stars over feeble ones.
Now, we have a luxury denied to astronomers of the early twentieth century: we can choose to examine the properties of a volume-limited or (nearly) complete set of stars. What does this mean? It means "pick all the stars that exist within some region of space", not just the bright ones. This will give a fair sample of the real population, including ALL stars, both feeble and powerful.
The graph below shows another sample from the Gaia database; this one consists of all the stars with a parallax of at least 20 milliarcseconds.
SELECT * FROM gaiadr2.gaia_source WHERE parallax > 20 and phot_g_mean_mag <= 17 and parallax_over_error >= 10
Q: If the parallax must be at least 20 milliarcseconds,
what is the maximum distance of these stars?
Right. The stars below represent all those within a sphere of radius 50 pc.
Q: How does this diagram compare to the 1914 version? Q: Can you explain the differences? Q: What is the ratio of giants to main-sequence stars here?
The HR diagram is a very useful tool: it shows us at a glance that
But why should stars break up into these groups? What's the difference between dwarfs and giants? And why are white dwarfs so different from all the other stars? Those are good questions, and kept astronomers occupied for the next several decades ....
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.