 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
So, suppose that we point our telescopes towards some distant star. It is so bright, and any possible planets around it are so faint, that we can only detect the light of the star itself.
Rats.
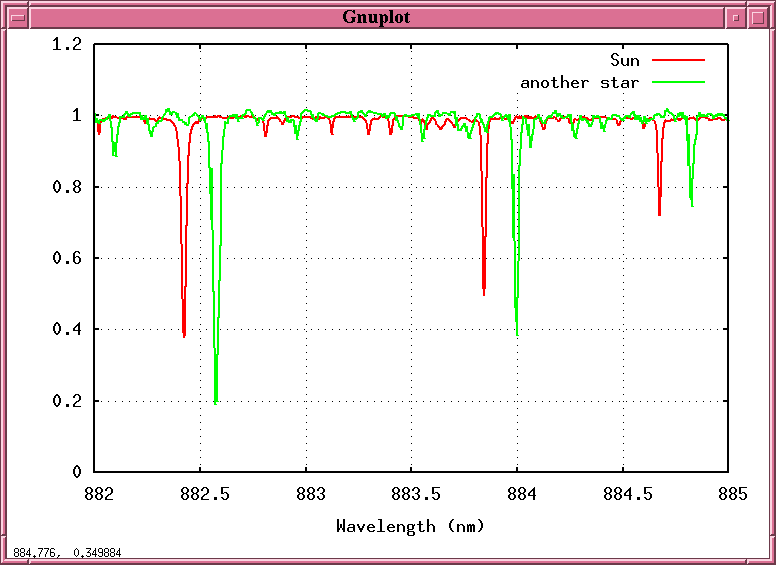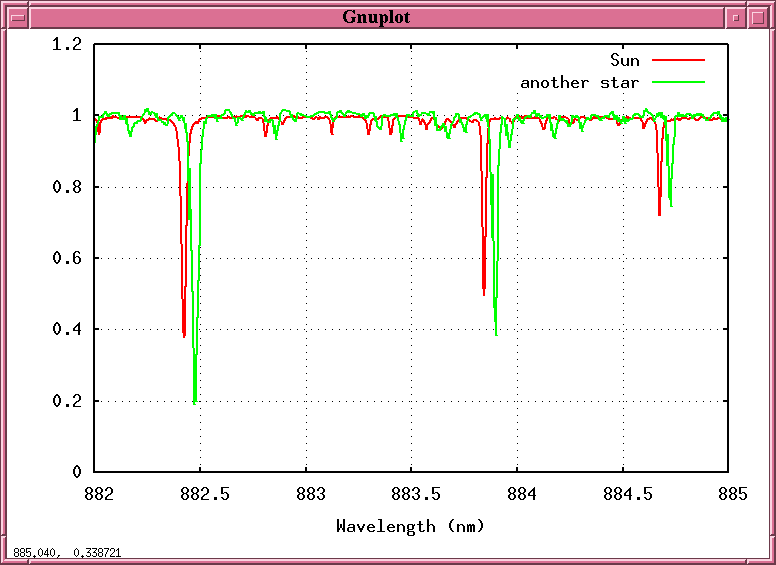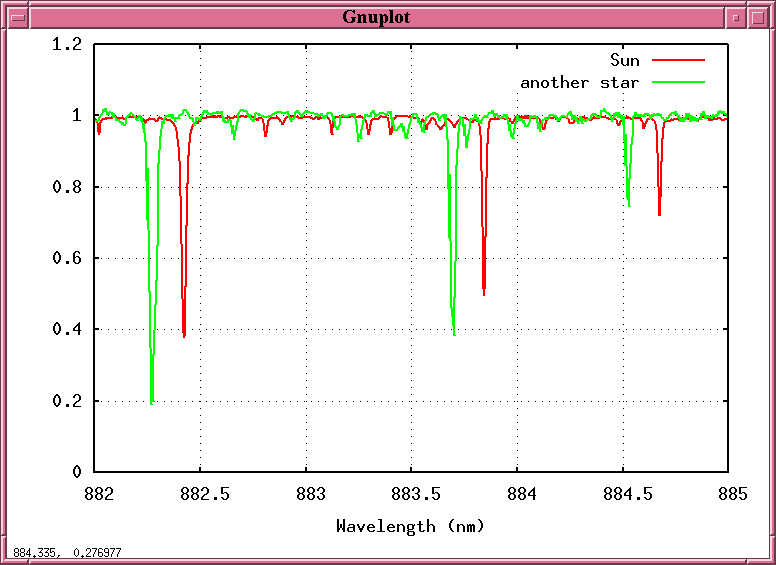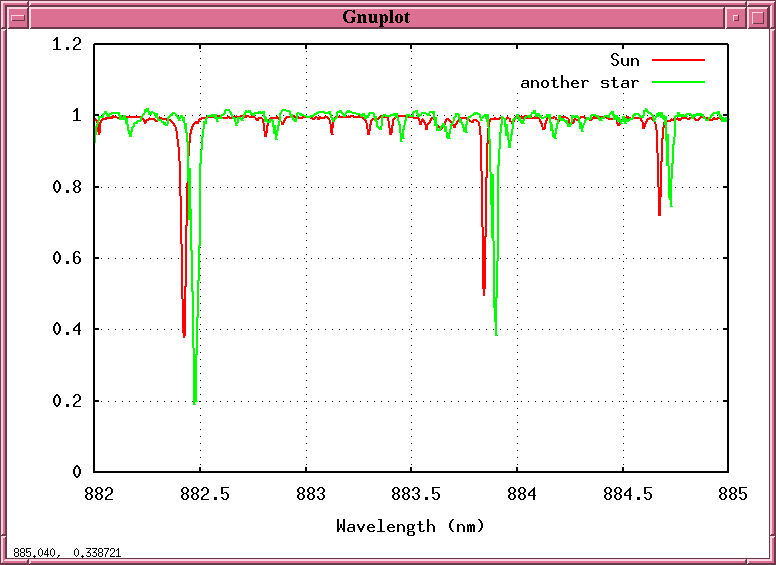
But suppose that we split this starlight into a spectrum and record it -- not just once, but over and over again, night after night, week after week. Maybe, just maybe, we might see the spectrum of that starlight change ....

Q: Why should the starlight shift back and forth,
back and forth, in a periodic fashion?
A: Because the star is moving towards us and
away from us, towards us and away from us,
as it circles around the center of mass
between it and a planet!
A little animation illustrating radial velocity curves
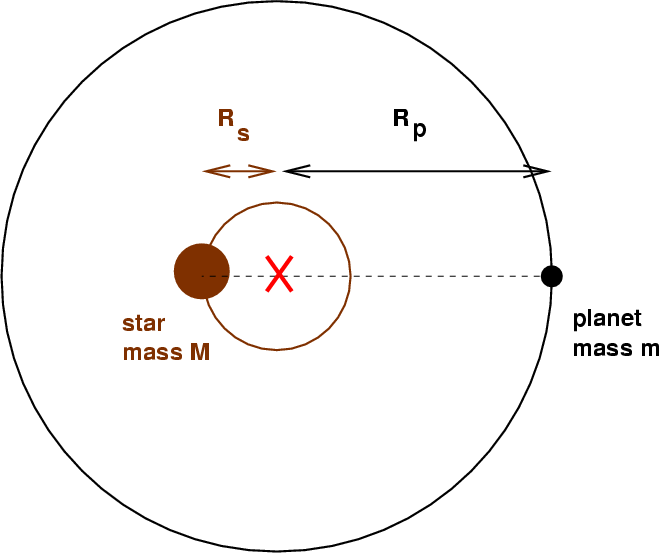
If you could figure out the size of the star's orbit, Rs, and if you knew the size of the planet's orbit Rp -- which is always much, much, larger -- then you could figure out the ratio of orbital radii, and, thanks to center of mass, the ratio of masses.
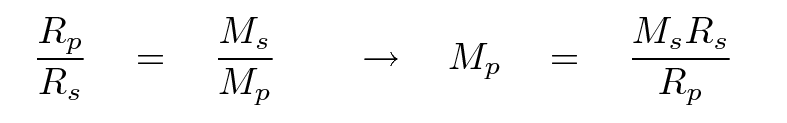
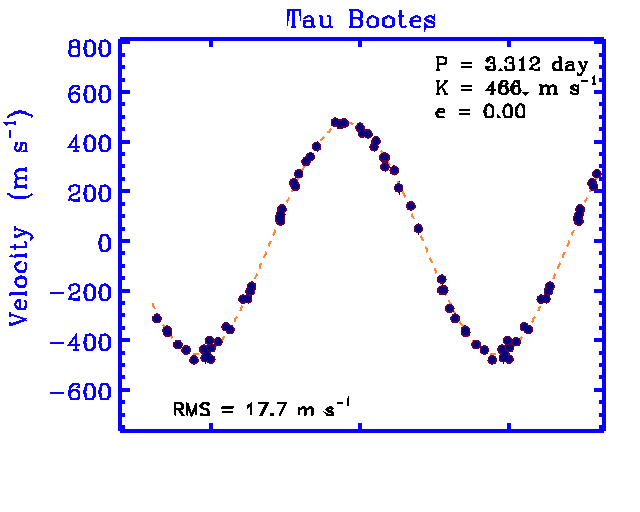
Look at the measurements of a star called "tau Bootes". This star is roughly the same mass as the Sun, so let's use Ms = 1.99 x 1030 kg. Measurements of its spectrum show that the star moves in a circle with a period of P = 3.312 days and a speed of about v = 466 m/s.
Now, the planet is circling the star with a much larger orbital radius Rp, but with exactly the same period P. How can we find its orbital radius? Let's assume that the star and the planet are both moving in perfectly circular paths. In that case, we can compute the star's centripetal accleration
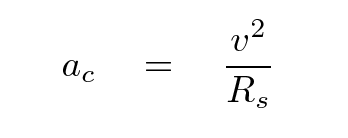
The acceleration is caused by the planet's gravitational force pulling on the star, so we could write
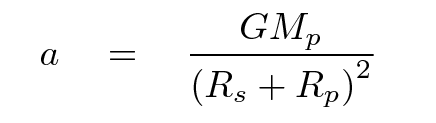
That leaves two unknown quantities, Rp and Mp, with just one equation. Fortunately, we have another equation relating these two properties of the planet, so we can substitute to end up with one equation for one unknown.
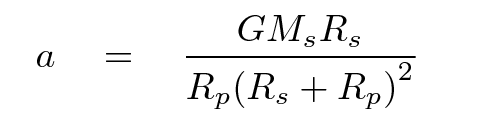
Because stars are much, much more massive than planets, we can assume that the distance of the planet from the center of mass is much, much larger than the distance of the star from the center of mass.

In other words,
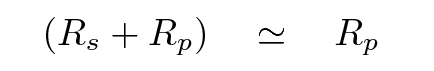
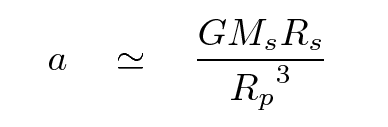
Excellent!
Now you can figure out the radius of its planet's orbit.
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.