 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.

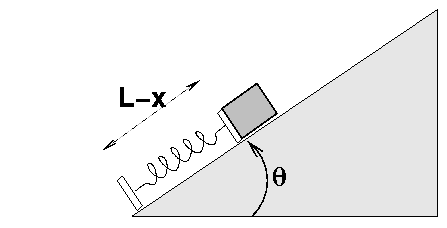
Just as before, an ideal spring of rest length L = 2 m and spring constant k = 120 N/m is placed on a ramp of angle theta = 20 degrees. This time, however, the ramp is not frictionless; instead, it has coefficient of kinetic friction muk = 0.07 . You then gently place a block of mass m = 1.5 kg onto the ramp and glue it onto the end of the spring. You push the block down until it compresses the spring by a distance x = 0.2000 m. You can feel the spring pushing back up against the block, so you have to hold the block in place.
You now release the block, and it starts to slide up the ramp.
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.