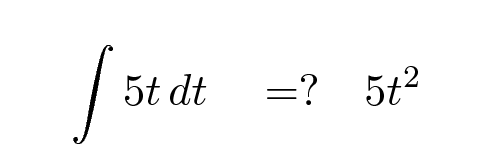
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
You've seen a couple of examples recently:
These are two illustrations of a general rule: if you integrate a function over time (or space), you end up with a result which behaves as a function to a higher power of time (or space).
In mathematical terms,
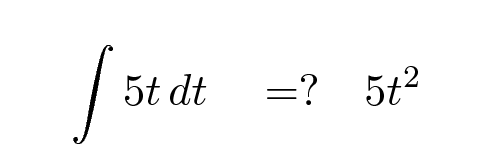
Is it really that simple? No, not quite. Integration and differentiation are opposites, in a very strict sense. If we integrate a function f(t) with respect to time, and then take the derivative of the result, we ought to end up with exactly the same f(t). That means that the simplest possible rule for integration won't quite work.
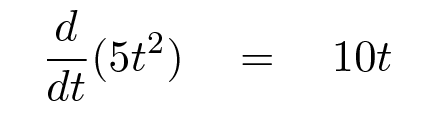
But you can force the derivative to end up at the right place by making the rule for integration just a little more complicated.
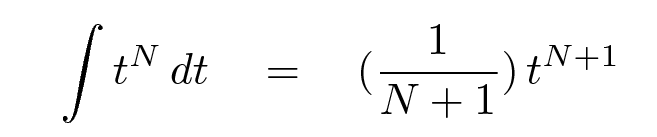
Let's do an example: can you perform this integral?
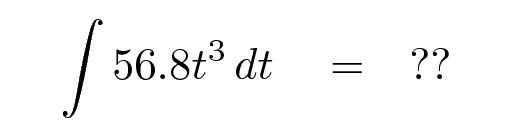
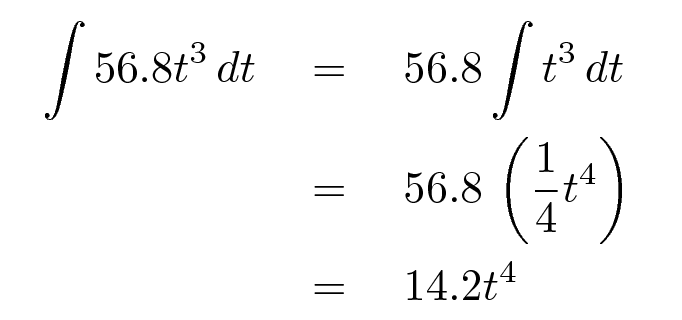
Remember that every integral occurs with respect to some quantity. If you add up the effect of some velocity over many little bits of time, then you are integrating with respect to time.
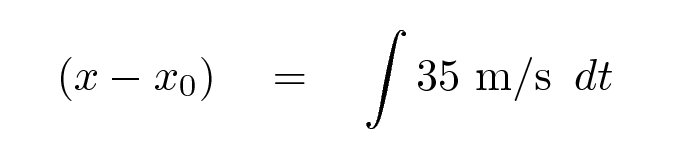
If you add up the mass of little bits of water which fill up the volume of a swimming pool, then you are integrating with respect to volume.
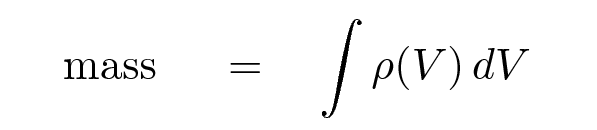
In many cases, you must not only figure out how to integrate some function, but, on top of that, you must then evaluate that integral over some range of time, or distance, or volume.
For example, suppose that a car is moving down the road at 30 m/s when suddenly a moose steps into view on the road ahead. The driver slams on the brakes so that the car decelerates at 3 m/s2. How far does the car slide forward over the next 2 seconds?
To find the distance the car travels, we need to integrate the velocity of the car over the 2 seconds of time. Since
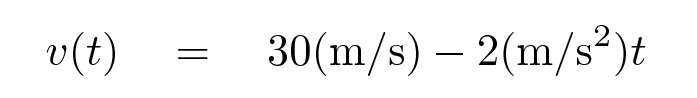
the integral we must perform looks like this:
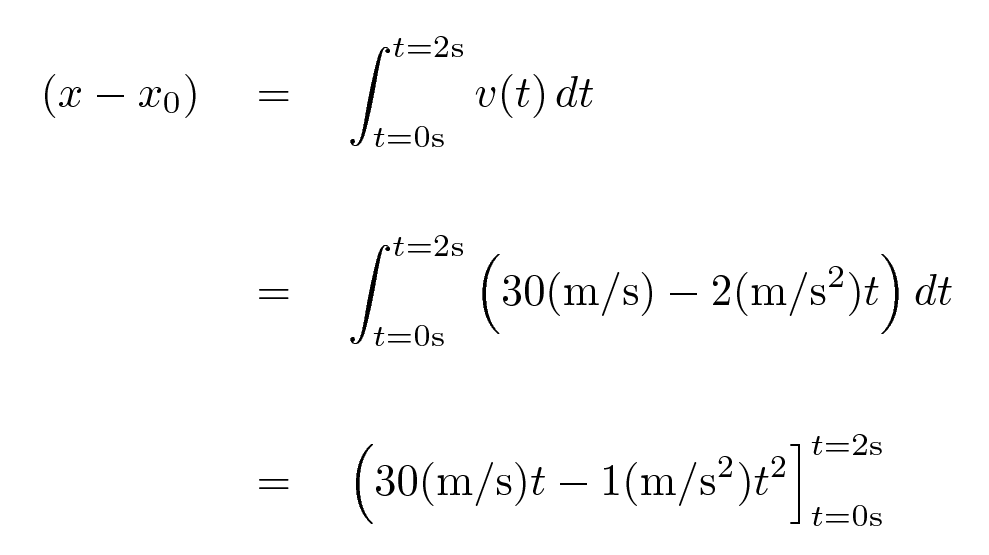
To evaluate an integral, write down two copies of the result: in the first copy, insert the ENDING time (or position, or whatever), and, in the second copy, insert the STARTING time (or position, or whatever). Work out the value of each copy, and then subtract the second from the first.
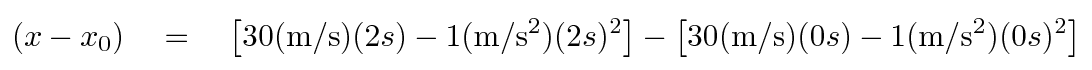
The distance the car travels between times t = 0 s and t = 2 s is 56 meters.
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.