newfile1

newfile1

What is the speed $v_{E}$ of the Earth's rotation?

$\displaystyle v_{E}=\frac{{40,000\mathrm{ km}}}{86,400\mathrm{ s}}=460\mathrm{ m/s}$

So the two planes fly at

$\displaystyle \mathrm{Red plane: }v_{E}+v_{J}=710\mathrm{ m/s}$

$\displaystyle \mathrm{Blue plane: }v_{E}-v_{J}=210\mathrm{ m/s}$

The $\gamma$ factor for each plane should be straightforward to compute, but in practice may cause a problem with some calculators. For the Red plane, we try

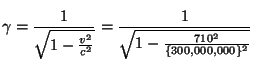
$\displaystyle \gamma=\frac{{1}}{\sqrt{{1-\frac{{v^{2}}}{c^{2}}}}}=\frac{{1}}{\sqrt{{1-\frac{{710^{2}}}{\{300,000,000\}^{2}}}}}$

but because $v\ll c$ , some calculators will yield $\gamma=1$ . In such cases, we need to use tricks based on the binomial theorem. First, for $\epsilon\ll1$ ,

$\displaystyle \sqrt{1-\epsilon}\;=\;(1-\epsilon)^{1/2}\;\simeq\;1-\frac{{1}}{2}\epsilon$

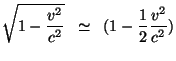
$\displaystyle \sqrt{1-\frac{{v^{2}}}{c^{2}}}\;\;\simeq\;\;(1-\frac{{1}}{2}\frac{{v^{2}}}{c^{2}})$

Second, again for $\epsilon\ll1$ ,

$\displaystyle \frac{{1}}{1-\epsilon}\;\;=\;\;(1-\epsilon)^{-1}\;\;\simeq\;\;(1+\epsilon)$

and thus

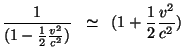
$\displaystyle \frac{{1}}{(1-\frac{{1}}{2}\frac{{v^{2}}}{c^{2}})}\;\;\simeq\;\;(1+\frac{{1}}{2}\frac{{v^{2}}}{c^{2}})$

That means that we can turn the expression for $\gamma$ into a form that we can handle easily - as long as we keep expressing it as ``1 plus something''. Watch:

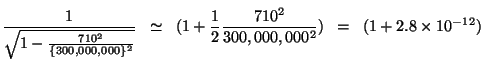
$\displaystyle \frac{{1}}{\sqrt{{1-\frac{{710^{2}}}{\{300,000,000\}^{2}}}}}\;\;\... ...1+\frac{{1}}{2}\frac{{710^{2}}}{300,000,000^{2}})\;\;=\;\;(1+2.8\times10^{-12})$

How long does it take the Red Plane, travelling around the world (a distance of about 40,000 km) at a speed of 710 m/s, to complete its journey? According to an observer motionless in space above the Earth's North Pole,

$\displaystyle t=\frac{40,000,000\mathrm{ m}}{710\mathrm{ m/s}}=56,338\mathrm{ s}$

somewhat less than a day. On board the Red Plane, however, the clock will run slower by a factor of $\gamma,$ so that it reads

$\displaystyle t_{R}=\frac{{t}}{\gamma}=\frac{t}{1+2.8\times10^{-12}}\;\;\simeq\;\; t(1-2.8\times10^{-12})$

The difference between the two clocks will be

$\displaystyle t-t_{R}$	$\displaystyle =t-t(1-2.8\times10^{-12})$
	$\displaystyle =t-t+t(2.8\times10^{-12})$
	$\displaystyle =t(2.8\times10^{-12})$
	$\displaystyle =1.57\times10^{-7}\mathrm{s}$
	$\displaystyle =157\mathrm{ ns}$

If you look at the papers describing this experiment, you'll see that the special relativistic effect indeed has roughly this size.

Michael Richmond 2003-12-05