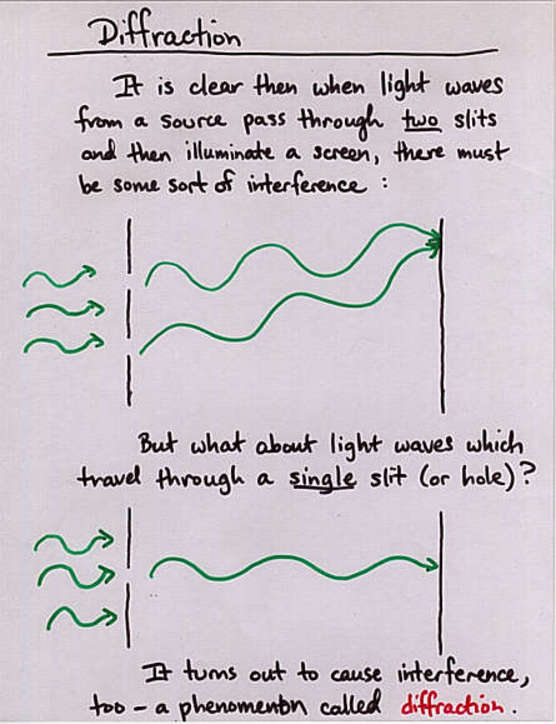
 Viewgraph 1
Viewgraph 1
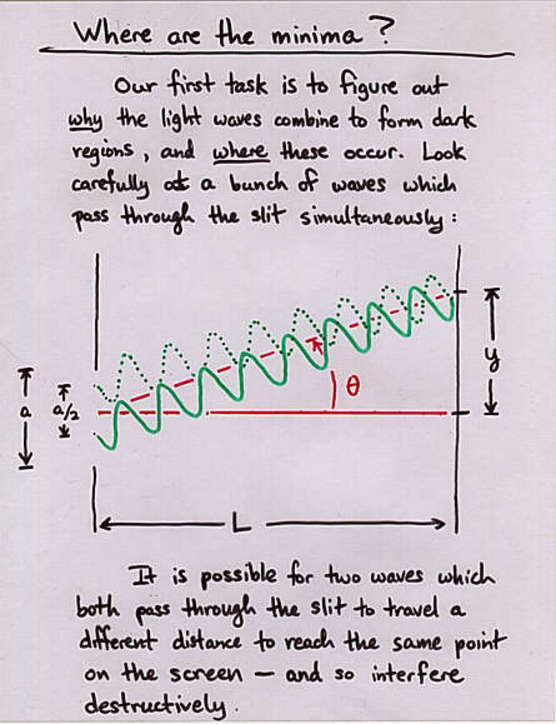 Viewgraph 2
Viewgraph 2
Why should there be two light waves separated by half the slit width? Well, when light encounters an obstacle, it acts as if new waves are created -- in a very particular way. Dutch astronomer and physicist Christian Huyghens came up with a model which helps one to understand diffraction and other effects: Huygen's Principle . Click on the picture below to see his idea in action.
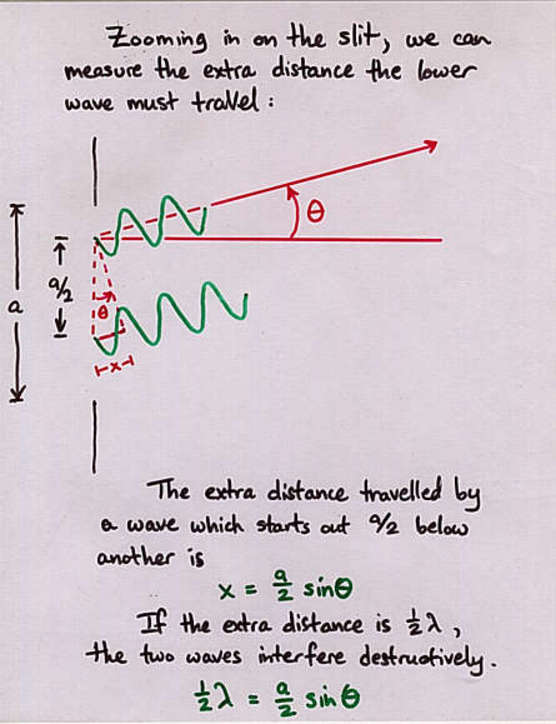 Viewgraph 3
Viewgraph 3
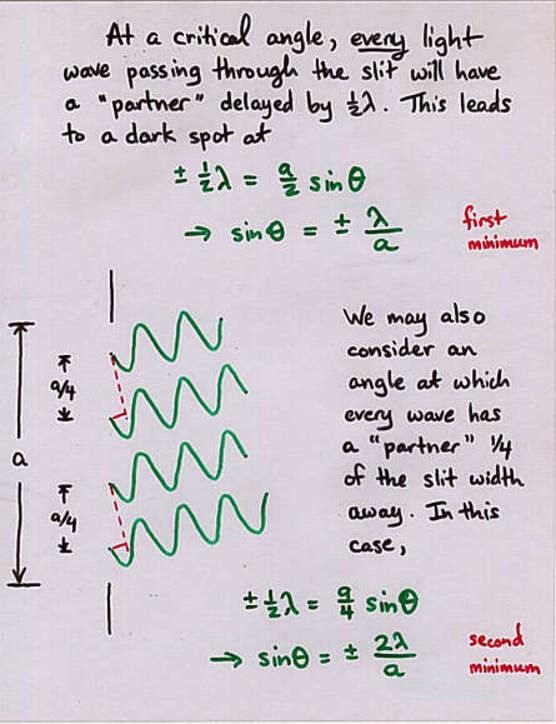 Viewgraph 4
Viewgraph 4
My explanation above -- and the one in your textbook -- draws a few light rays and compares the distance each one travels on its way to the screen.
But there are other ways to think about diffraction. One can start with Huygen's Principle, for example: draw the spherical wave fronts created at two points within the slit, following each wave front as it marches forward.
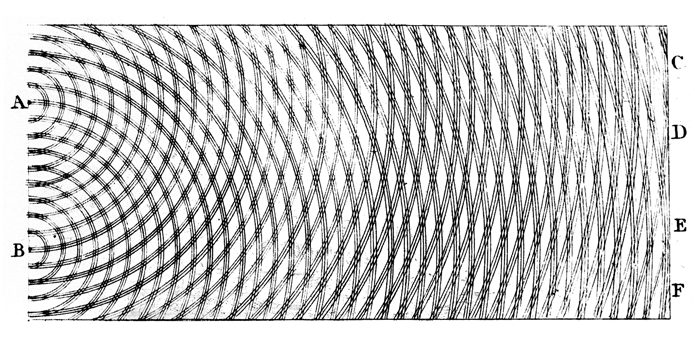
(This illustration comes from Thomas Young's paper to
the Royal Society of London, published in 1803!)
 Viewgraph 5
Viewgraph 5

 Viewgraph 6
Viewgraph 6
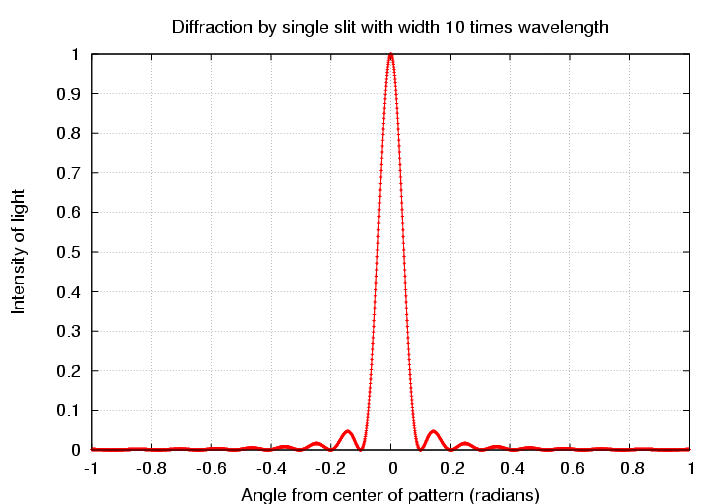
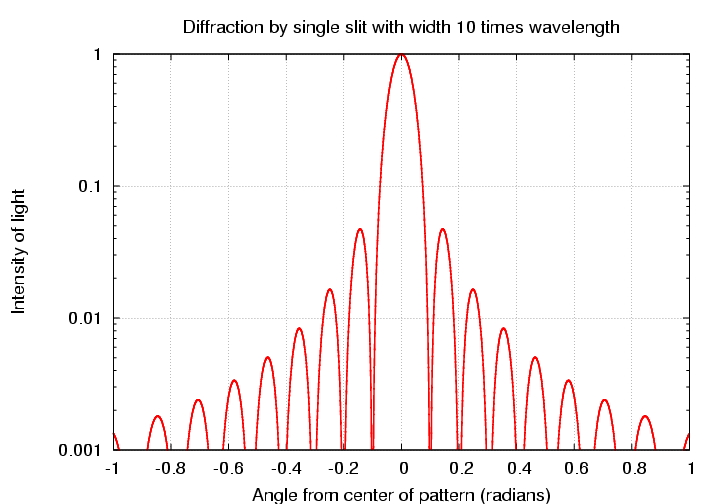
How does this pattern compare to the pattern of spots produced by two-slit interference? Let's compare them
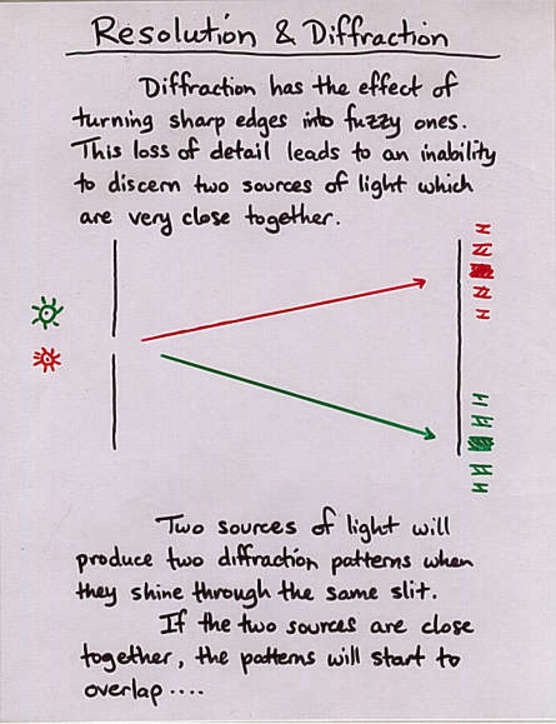 Viewgraph 7
Viewgraph 7
 Viewgraph 8
Viewgraph 8
Consider the painting "A Sunday on La Grande Jatte" by Georges Seurat.
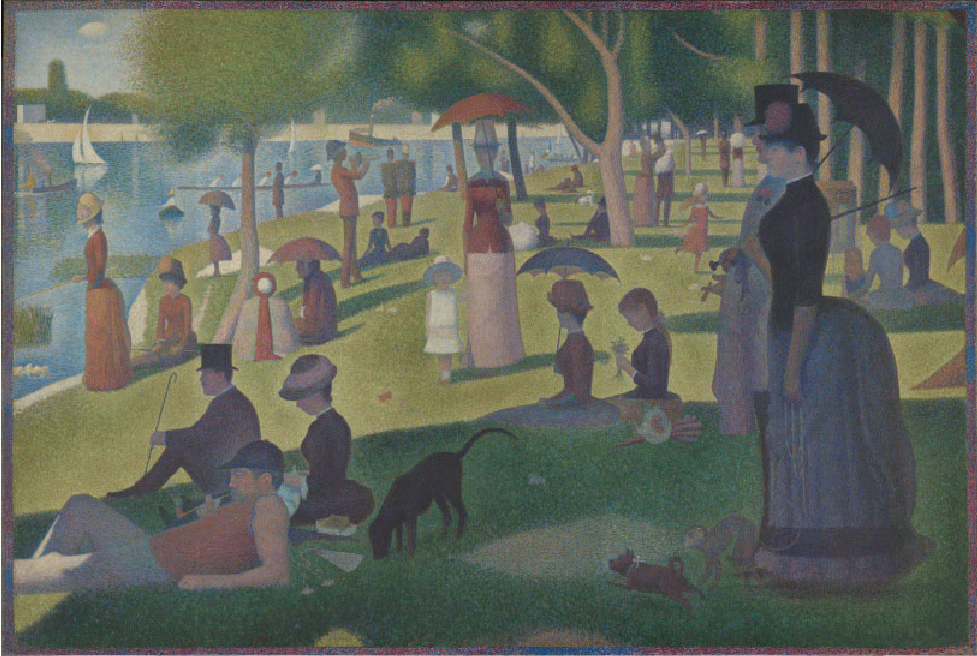
It appears to be an ordinary painting, showing green grass, pink dresses, red shirts, and so forth. But if you look very closely at a little section of the painting, like this one:
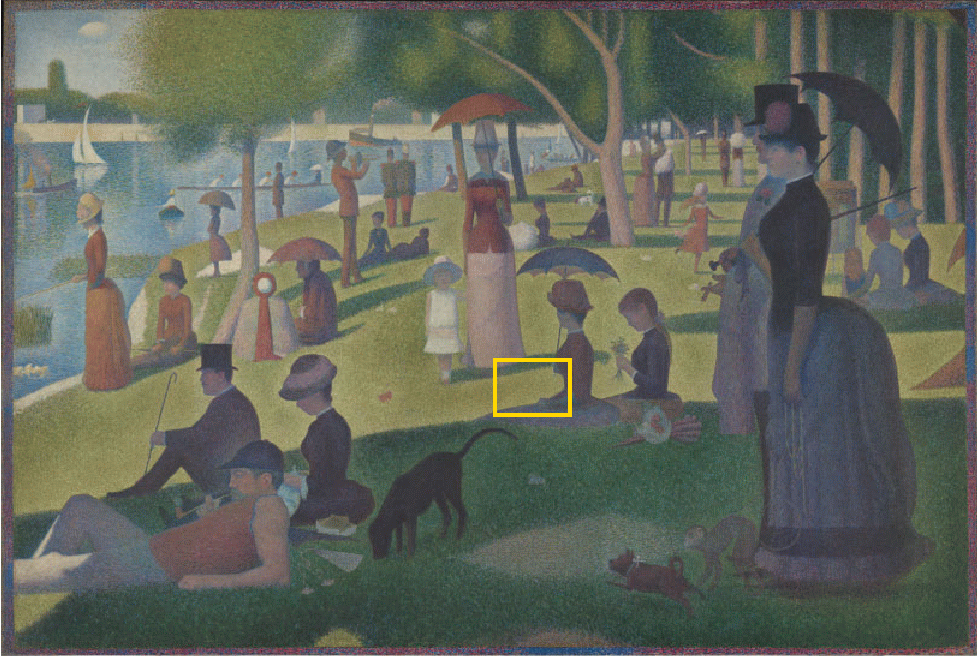
you will see that it consists of a set of little daubs of paint.

 Viewgraph 9
Viewgraph 9
 Viewgraph 10
Viewgraph 10


