Using impulse to find velocity

In this experiment, you will measure forces exerted over time on a cart as it bounces off an obstacle. You can calculate the impulse and use it to find the velocity of the cart just before and after the impact. You can even go on to figure out the coefficient of rolling friction between the cart and the track.

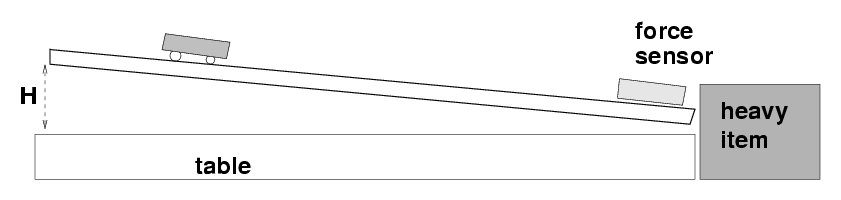
Set up a track so that one end is slightly higher, H = 3-4 cm, above the other end. Place a force sensor at the bottom end, with its hook screwed all the way into the sensor. Put a block into the force sensor to hold it in place (you might even tape it into place on the track). Make sure that a heavy item sits next to the bottom end of the track to prevent the track from sliding across the table (or hold the track during each run).

calibrate the force sensor on its +/- 50 N setting
measure the tilt of the track accurately
in the "Student Shares" -> ... -> "LabPro" folder, click on the impulse_friction file
arrange the cart so that its spring-loaded bumper is extended and will bump into the force sensor's hook

Put the cart at some known distance around 60-70 cm from the sensor. Call this your "starting point."

If there were no friction, how fast would the cart be going when it bumps into the sensor?

Now, to make one set of measurements, release the cart from its starting point and start collecting data. You may have to wait until the collection is finished for the data to appear on your screen. The cart should roll down, bump into the force sensor, bounce off and roll back up the ramp. Watch carefully and mark the location it reaches at the apex of its motion. Let it roll back down and bump into the sensor again, and then again mark how far back up the ramp it goes. Record the positions for the first 2 bounces. The cart will end up motionless at the bottom of the track.

draw a series of three pictures showing the cart and sensor just before, during, and just after they collide
what is the impulse imparted to the cart by the sensor from the first collision?
what was the speed of the cart just before and after the first collision? (you may assume that the collision was "elastic", meaning no energy was lost)

Compare this measured speed to the speed you calculated earlier. Are they the same?

calculate the KE the cart should have had, theoretically, when it reached the bottom of the track, and the KE the cart did have, based on its actual speed
use the difference in KE to figure out the work done by friction as the cart was moving down the track
figure out the force of friction on the cart during its motion down the track
use the force of friction to determine the coefficient of friction on the cart

Repeat your analysis for bounces 2 and 3: use the distance the cart rolled before hitting the sensor to figure out what its speed should have been, and the impulse to figure out what its speed really was.

is the force of friction the same each time?
is the coefficient of friction the same each time?

Make three trial runs. Create a table showing all your results. How consistent are the results from one run to the next?

Hand in your answers to all these questions, written neatly. Include a table with ALL your measurements, and include all your calculations, too.