 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Collisions in two dimensions
All the examples you have considered so far involve
motion in a single dimension, along a track or a road.
What happens when objects are free to move and bounce
in two or three dimensions?
It turns out that momentum is (in the absence of external forces)
conserved in each direction individually.
In other words,
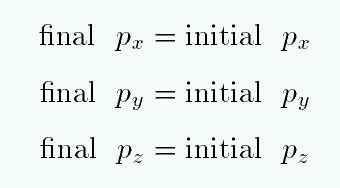
or, in more compact notation,
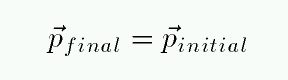
Example of a two-dimensional collision
Use your computers to analyze a video in which two pucks
collide on an air table.
You might want to read the
instructions for marking
properties on videos in LoggerPro.
- Go to the "Student Shares" -> ... "LoggerPro" -> "CofM Video" folder.
- Double-click on the 1D_CoM_P017 file. It shows a collision
between two pucks of different mass on an air table.
- What is the momentum of each puck in each direction (x, y)
before the collision?
- What is the magnitude of the momentum of each puck before
the collision (i.e. the combination of x and y components)?
- What is the total momentum in each direction before the collision?
- What is the momentum of each puck in each direction (x, y)
after the collision?
- What is the magnitude of the momentum of each puck after
the collision?
- What is the total momentum in each direction after the collision?
- Is the total momentum conserved in each direction?
If not, there must
be some external forces acting on the pucks.
What are the most likely suspects?
- If you add the magnitudes of the momentum of each object
before the collision, and then after the collision,
do you find the same value? Why not?
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
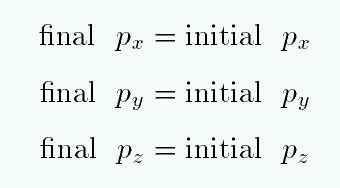
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
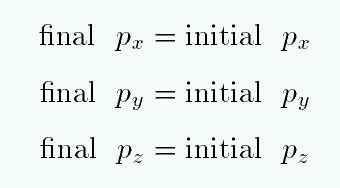
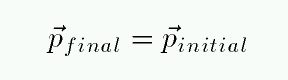
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.