 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Preparing for the Conservation of Energy exercise
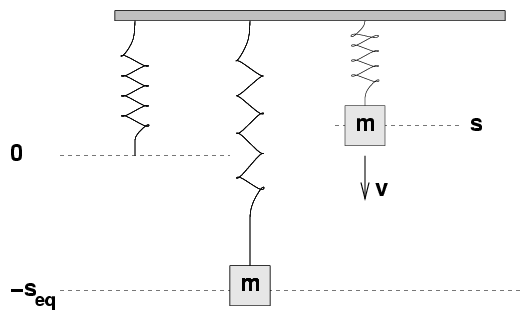
Consider a spring hanging at rest from a rod.
If left to itself, it has some rest length.
We could define a coordinate system based
on vertical distance S above this rest length.
By placing a block of mass m onto the end
of the spring, we force the spring to stretch,
so that its end is a distance Seq below
the rest length.
- Solve for the magnitude of the equlibrium distance Seq in terms
of m, g and the spring constant k.
- Suppose the block is a distance s above the rest length
and moving with a speed v;
what is its total mechanical energy?
Place the zero point of gravitational potential energy
at the rest length.
Your answer should have three terms: one for GPE,
one for SPE, and one for KE.
Now, suppose that we instead decide to measure
distances from this equilibrium position.
(It will turn out to make our calculations simpler if we do this.)
We'll use the coordinate y to denote
"distance above the equilibrium position."
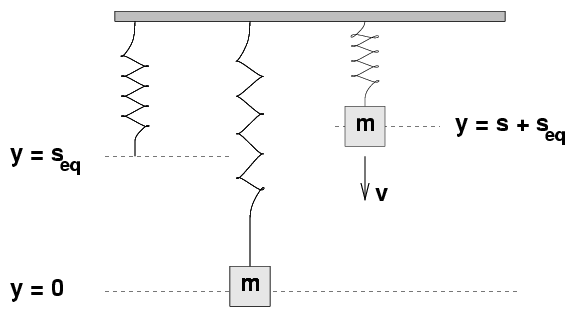
With this choice of coordinate, it makes sense to place
the zero point of GPE at the equilibrium position y = 0.
Once again, consider the situation when the block is a distance
s above the rest length, and moving downwards
with a speed v.
- Suppose the block is a distance s above the rest length
and moving with a speed v;
what is its total mechanical energy?
This time, place the zero point of gravitational potential energy
at the equilibrium position.
Your answer should have three terms: one for GPE,
one for SPE, and one for KE.
- Now, using your algebraic skills,
show that you can express this total energy in the form
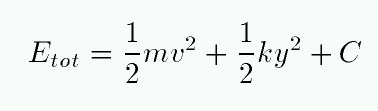
where C is some constant, a combination of m, g
and k.
In other words, show that the total energy can be
computed from two terms which change as the spring moves --
one is kinetic energy, the other a combination of spring
and gravitational potential energy --
plus one term which remains constant.
- For the purposes of today's experiment, we will set the
energy scale so that it has a value of zero when the block
is motionless at the equilibrium point.
What is the value of the constant C?
So, the way we've defined total mechanical energy in this
experiment,
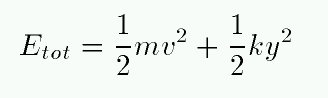
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.

 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.


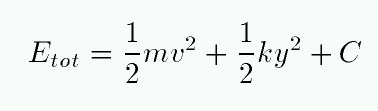
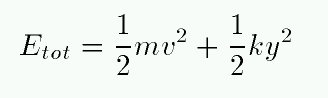
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.