 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Work done by the (changing) force of gravity
An object of mass m on the Earth's surface
is pulled downwards by the Earth's gravity.
The size of this force is
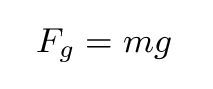
where g = 9.8 m/s^2 (approx) is the local acceleration
due to gravity.
However, if you climb up a very tall mountain, you will find
that this gravitational force becomes a bit weaker.
On the top of Mount Everest, you'll weigh just
a bit less than you do at sea level.
Why is that?
The answer is that the force of gravity between
two objects depends on the distance between them.
The general form of this force is
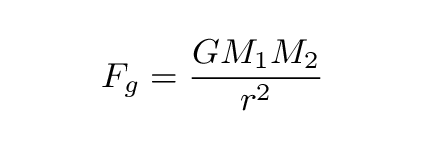
- Use this formula to calculate the force between Joe (m = 60 kg)
and the Earth, when Joe is standing on the Earth's surface.
Appendix C in your textbook might help with some of the numbers ...
- If Joe drops a ball while standing at sea level,
how fast will it accelerate?
When you walk up Mount Everest, you increase the distance
between you and the center of the Earth.
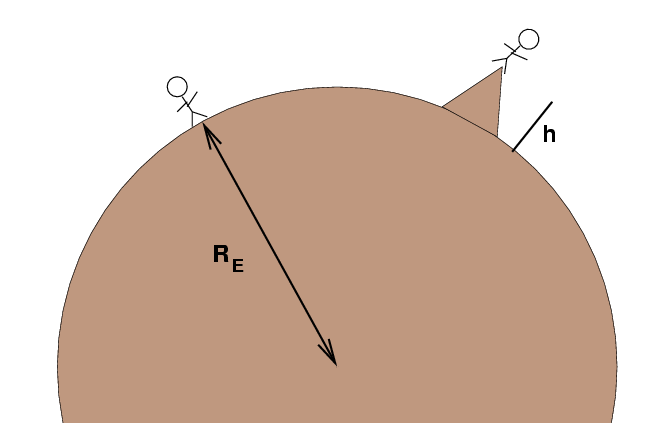
- Mount Everest is about h = 8000 m tall.
What is the Earth's gravitational force on Joe when
he stands on Mount Everest?
- If Joe drops a ball while standing on the top of the
mountain, how fast will it accelerate?
So the force of gravity on Joe is NOT constant in size:
it keeps decreasing slightly as he moves farther and
farther away from the center of the Earth.
Therefore, in order to figure exactly how much work he does
to climb upwards, you can't simply
multiply "force times distance."
Instead, you need to integrate ...
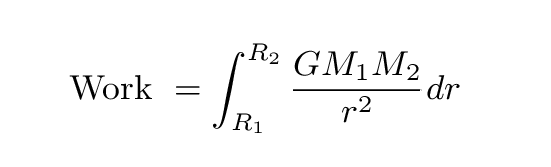
- Joe finds a convenient ladder which goes vertically
up from the base of Mount Everest to its peak.
How much work must he do to climb from the bottom
of this ladder to the top?
- A single Big Mac contains about 560 calories.
The ordinary "calorie" we use in conversation
is equal to 4186 Joules of energy.
How many Big Macs must Joe eat to replenish himself
on his 8000 m climb?
- At the top of the mountain,
Joe finds another ladder which climbs vertically
into space, halfway to the Moon.
"Cool!" thinks Joe, "I've always
wanted to into space!"
How much work must he do to climb from the bottom
of this ladder to the top?
- When Joe reaches the top of this ladder,
he gets out his camera to take a picture.
Unfortunately, he drops the lens cover,
which falls back towards the Earth.
How fast does it accelerate as it falls?
(Yes, yes, there would be complicating effects
due to the rotation of the Earth and the ladder.
Let's ignore them for now ...)
For more information
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
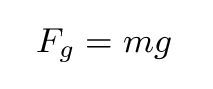
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
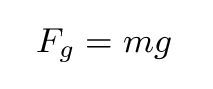
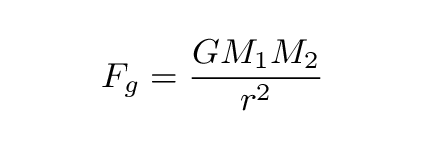

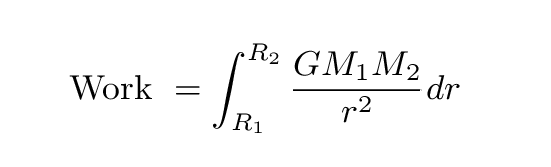
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.