 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
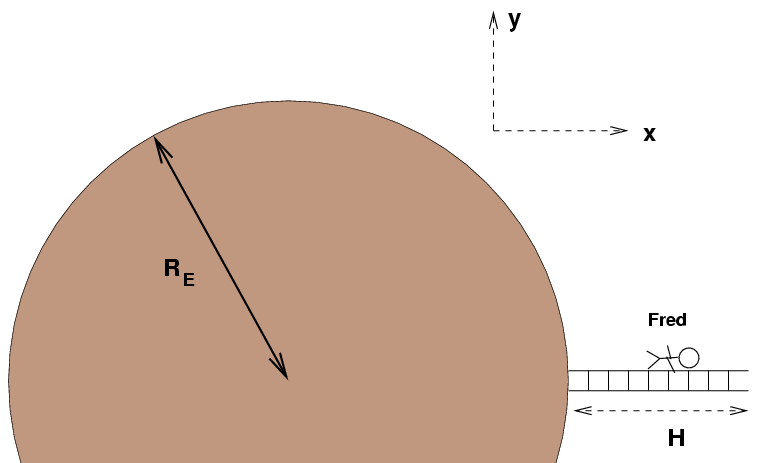
If you move vertically by a significant distance, the force of the Earth's gravity on you changes: it keeps decreasing as you move farther and farther away from the center of the Earth.

Therefore, in order to figure exactly how much work you do while, say, climbing up a ladder, you can't simply multiply "force times distance." Instead, you need to integrate. For example, if we want to compute the amount of work done by the force of gravity on Joe as he climbs the ladder, we would write down this integral. Note the signs of the two terms in the integral, which indicate the direction of the force, and the direction of the motion.
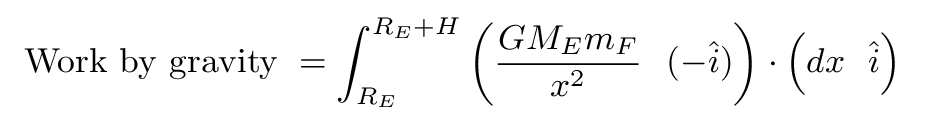
On the other hand, if we are interested in the work done by Joe as he climbs the ladder, it's a bit different. We know that the size of the force Joe must exert on the ladder to lift himself up is the same as the size of the force of gravity on him, but it points in the other direction -- AWAY from the Earth.
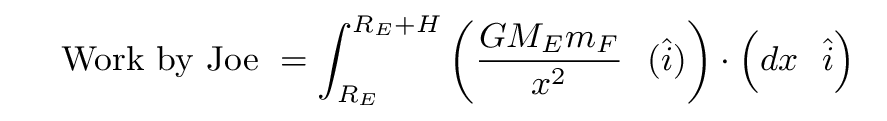
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.