The dependence of air resistance on velocity

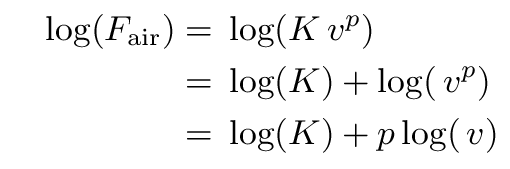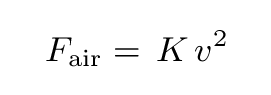
The force of air resistance clearly depends on the velocity of an object moving through the air: the larger the speed, the larger the drag force. But what is the exact form of this relationship?

Your textbook suggests that under some circumstances, air resistance depends on the square of the velocity:

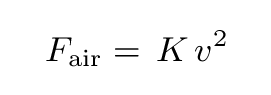
However, some other sources suggest that at low speeds, the air resistance grows linearly with velocity:

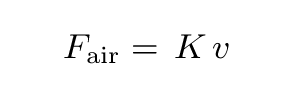
Your job today is to figure out which of these formulae more accurately fits the data from a simple experiment.

The experiment

Each team will make measurements of the same event: I'll drop one set of filters, and the entire class will share all the resulting measurements.

• Create a set of objects with the same size and shape, but different mass, by placing paper clips. We'll use 0, 1, 2, 3, 4, and 5 clips placed into a single filter.
• Give the objects what we HOPE will be terminal velocity by dropping them from the third floor of the atrium. After a short acceleration, each one will (we hope) reach a constant speed for the majority of its fall.
• Have a team member stand on the staircase in the middle of the atrium and measure the time it takes for each stack to fall from the top of the first-floor railing to the bottom of the atrium.
• Make two trials for each stack.
• Calculate the speed of each stack during this final portion of its flight; the distance from atrium floor to first-floor railing is 5.8 meters.

You'll need to know the masses of the objects involved:

• the mass of one filter is 1.6 grams
• the mass of one paper clip is 0.4 grams

The model

When an object has reached terminal velocity, the downward pull of gravity exactly balances the upward push of air resistance:

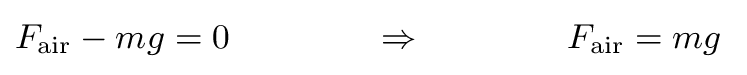
That means that you can calculate the force of air resistance easily, if you know the mass of the falling filters.

Now, your job is to determine which of these relationships between the force of air resistance and velocity is a better fit to your measurements.

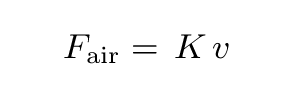
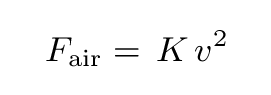
A good way to see if measurements match a theory is to make a graph on which the theory predicts there should be a straight line:

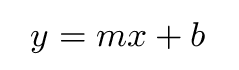
If the data lie in a line on the graph, then they agree with the theory. The slope of that line must correspond to the symbol m in the equation, and the y-intercept of the graph must correspond to the symbol b.

Suppose that a coffee filter had a very tiny mass; for example, 0.001 grams. What would the force of air resistance be on that filter when it reached terminal velocity?

1. If you wanted to test the first theory, in which air resistance goes like velocity, what variable should you put on the x-axis of a graph? What variable would go on the y-axis of the graph?
2. Have one person make such a graph. Start the graph at a velocity of zero, and expand the axes to include all the measurements. Do your measurements lie in a straight line on this graph?
3. If you wanted to test the second theory, in which air resistance goes like velocity-squared, what variable should you put on the x-axis of a graph? What variable would go on the y-axis of the graph?
4. Have one person make such a graph. Start the graph at a velocity of zero, and expand the axes to include all the measurements. Do your measurements lie in a straight line on this graph?

Make a prediction: if we were to place 8 clips into a filter, and drop it, what terminal velocity would it reach? How long would it take to fall from the first-floor railing to the floor of the atrium?

If you have time, consider ...

Log-log plots and power laws

We have only considered two very simple possibilities, in which the the force of air resistance depends on velocity to the first power, or the second power. It's quite possible that real life may be more complicated: maybe air resistance depends on some fractional power of the velocity, like

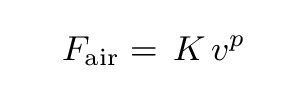
When physicists think that one quantity depends on some other quantity raised to a power, they often turn to log-log graphs. Starting with a formula in which velocity goes like some power n of the mass, they take the logarithm of both sides, and then make a graph based on that new equation.

1. Make a graph based on the final form of the equation above; you will need to make a table showing the logarithms of your measurements.
2. Fit a straight line to the data in this log-log graph. What is the equation of the line? What is the value of the power p based on this method?
3. Which of our simple models -- air resistance going like velocity or velocity-squared -- does this method support?