Using a tilted Atwood's machine

The goal of today's experiment is for you to determine

an approximate value for the local acceleration due to gravity, g, using a graphical method of analysis
a value for the coefficient of rolling friction for a cart on a track, using a non-graphical method of analysis
uncertainties for each value

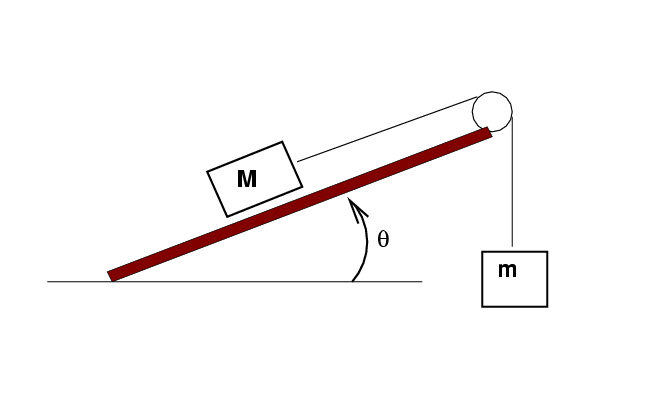
Clean your track gently with a damp paper towel, then dry it off. Tilt it at an angle of between 3 and 5 degrees; any value in that range is okay, just make sure you measure it properly and stabilize the track so it won't move. Place a cart on the track. Connect this cart to a hanging mass (use the blue mass sets) via a pulley.

Add mass to the cart in the following manner:

the cart itself
two mass bars on top
six pennies, held onto the bars with tape

Measure the mass of the cart and all its cargo on a scale. We'll call this cart mass M.

Add weights to the hanger so that its total mass is about 115 grams; we'll call the hanging mass m. Adjust this hanging mass so that the cart will slowly roll up the ramp, taking about 5 seconds to cover a distance L = 60 cm.

Measurements

Your job is to measure the acceleration of the cart up the track. In each case, you'll measure the time it takes for the cart to travel L = 60 cm, and you should make three trials for each case. The trick is that you will make measurements while varying the mass of both the cart and the hanger, by transferring pennies, one at a time, from cart to hanger. So, you should make measurements with:

6 pennies on cart, 0 on hanger
5 pennies on cart, 1 on hanger
0 pennies on cart, 6 on hanger

Note that the total mass, M + m, remains the same. All you are doing is moving some mass from the cart to the hanger.

In every case, the time it takes for the cart to roll L = 60 cm should be more than 2 seconds. Check with the instructor if you can't make this happen.

Make a table of your all your measurements, showing the cart mass M and hanging mass m as well as the times and accelerations.

Preliminary analysis:

Draw a free-body diagram for the cart.
Draw a free-body diagram for the hanging mass.
Make tables showing all forces acting on each object.
Write down two equations, one for the forces acting on the cart parallel to the ramp, one for the forces acting on the hanging mass vertically.
Eliminate the tension force T from the two equations, leaving one equation. This equation should include acceleration and coefficient of rolling friction, as well as other terms.

Use a graph to find an approximate value for "g" (and its uncertainty)

Use algebra to put your equation into a form that looks like this:




     acceleration   =    ( some stuff ) * m     +    ( other stuff )

Now, the first term on the right-hand side changes when you add pennies to the hanger, because m gets bigger; but the second term doesn't change (much) at all as you move pennies. That means that if you make a graph which has hanging mass m on the horizontal axis, and acceleration on the vertical axis, the slope of a line through your data should be equal to the "(some stuff)" term.

Make a graph showing all your measurements
Fit a straight line to your measurements
Use the slope of that line to figure out the local acceleration due to gravity, plus an uncertainty

Your value may not be very accurate, due to a not-quite-valid assumption made in the paragraph above. Can you explain?

Use calculations to find a value for coefficient of friction

Use algebra to put your equation into a form that looks like this:



                            (some stuff)   -  (some other stuff)
          mu        =    --------------------------------------------
                                    (stuff on the bottom)

In this case, you won't make any approximations. Adopt the proper value for g = 980 cm per second per second , and make a neat table. For each trial of your measurements, compute a value of mu. I had three trials each for seven different mass combinations, so a total of 21 values.

After you have finished, compute a mean value and an uncertainty for this coefficient of rolling friction. The uncertainty in my value was about 15 percent; can you do as well?

Each group must submit a single lab report at the start of our next class (it's okay to hand it in earlier, of course!). The lab report must contain

title, name, date
picture(s) of the setup
table(s) of all measurements, including units
sample equations showing calculations (just provide one example for each type of calculation)
a graph showing acceleration plotted against the hanging mass
derived value of the local acceleration due to gravity, "g", with uncertainty
derived value of the coefficient of rolling friction, "mu", with uncertainty
comments on the values you derived; for example, does your value of "g" agree with the usual value within the experimental uncertainties?
one suggestion for improving the experiment -- what could you do differently to make the results more accurate?

I will judge each report on a number of criteria, which include grammar, spelling, and neatness.