Your job in this exercise is to watch very carefully as a ball is shot out of a gun, flies through the air, and lands on the floor. After you have analyzed its motion, you must predict where and when the ball will land when shot at a different angle.

Here's the basic setup:

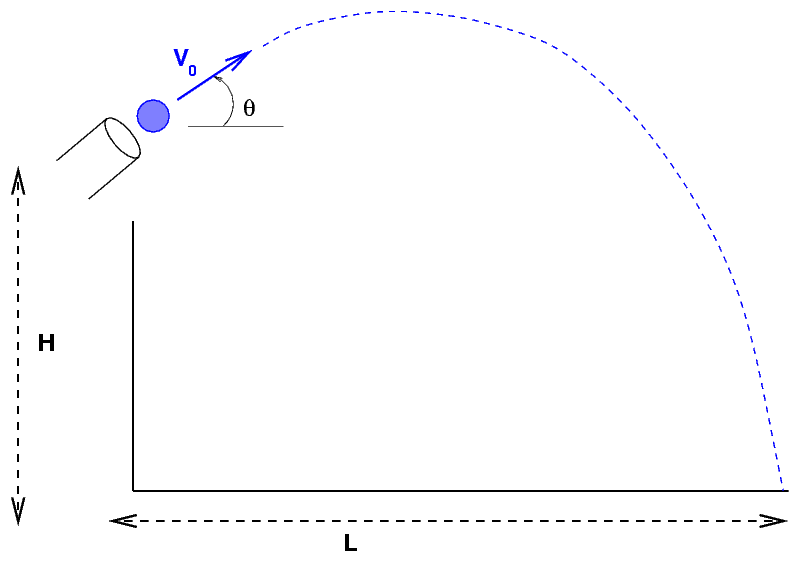
I will set up a single cannon (one of the ballistic pendulum devices) in the middle of the room, on top of a table. I will tilt the barrel of the gun by an angle theta = 45 +/- 3 degrees and fire the cannon at its "long range" setting. I will fire the cannon three times so that the ball falls onto a piece of paper in a cardboard box. A student will mark the location at which the ball strikes the box each time. We'll write all the measurements on the board. Then, each group independently must

1. using the height H and total length L, determine the speed v at which the ball leaves the cannon. It will help if you can figure out a single equation which has v on the left, by itself, and a bunch of stuff on the other side involving no time, just H, L, θ and g.

2. compute the uncertainty in the initial speed v. This will take four or five steps; feel free to ask for help. It will help to first fill out the uncertainty worksheet.

3. calculate the time of flight t of the ball When you reach this point, ask me for the actual time of flight. Do your computations match reality? Discuss. If you have oodles of free time, try to calculate the uncertainty in the time of flight

4. Now, suppose I change the angle of the barrel to theta = 65 +/- 3 degrees. Predict
   • the new distance the ball will travel -- it will help if you re-arrange the equation from step 1 to solve for L in terms of the other quantities. Yes, it will require the quadratic equation.
   • the new time of flight
   • if you have time, the uncertainty in new distance
   • if you have time, the uncertainty in new time of flight

Near the end of the class period, I will make the shot at the new angle of theta = 65 degrees, and we'll see how well you do.

Each group must hand in at the end of class:

• a sheet of graph paper with a neat diagram showing the experiment
• a table with all the measured quantities and their uncertainties
• an equation showing how to determine the initial velocity v
• the value of v
• the uncertainty in your value of v
• the value of t for angle θ = 45 degrees; does it agree with the measured time?
• an equation showing how to compute the new horizontal distance the ball will travel at the new angle of θ = 65 degrees
• your predictions for the new value of horizontal distance and new time of flight
• the actual new horizontal distance and new time of flight; how close were your predictions?