 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Predict the landing spot of a car
Your job in this exercise is to watch very carefully as a
little car rolls off a table, flies through the air,
and lands on the floor.
After you have analyzed its motion, you must predict where
the car will land when given a different initial velocity.
Here's the basic setup:
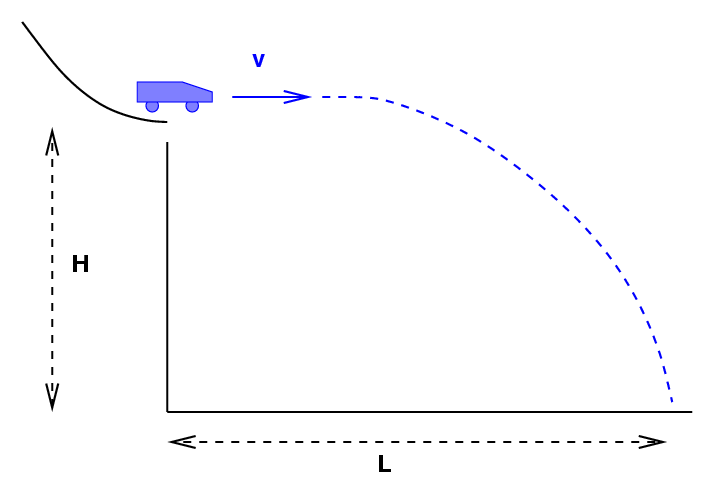
I will arrange the track, car, and other material
on the front table.
I will make careful measurements of the
height H +/- ΔH of track above the floor,
and the distance L +/- ΔL from the end of the track
to the landing point.
- Calculate the time the car spends in the air
together with the uncertainty in this time.
Explain to me in writing your method, and show all
your work.
- Compute the initial velocity of the car
when it leaves the track.
Include the uncertainty in this velocity.
- Write an equation which describes the range of the car
for any initial velocity.
Assume that the height H
remains the same, but the initial velocity vi
is
3 m/s, or 5 m/s, or 20 m/s.
How far would the car go?
- Write an equation which describes the range of the car
for any initial height.
Now assume that the initial velocity
is fixed at the value we calculated in step 2,
but the height of track H
is 1.2 m, or 5 m, or 13 m.
How far would the car go?
- Predict the distance the ball will travel
if given an initial velocity of 2.0 +/- 0.2
times the value from step 2.
Be sure to include an uncertainty in this distance:
for example, "the ball will travel
56 +/- 3 cm", or something like that.
How do you deal with combining two measurements, each of which
has an associated uncertainty?
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.

 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.

 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.