How to deal with collisions

Two objects smash into each other. What happens afterwards? And how do you figure it out?

That's a very general description. The method of attack will depend on the details of the situation. General rules to keep in mind are:

• momentum is always conserved in the absence of external forces
• momentum is a vector, so initial Px equals final Px, initial Py equals final Py, etc.
• kinetic energy is sometimes conserved; we use the word "elastic" if KE is the same before and afterwards, and the word "inelastic" if it changes
• kinetic energy is a scalar, so initial KE equals final KE with no directions

Let's do some examples.

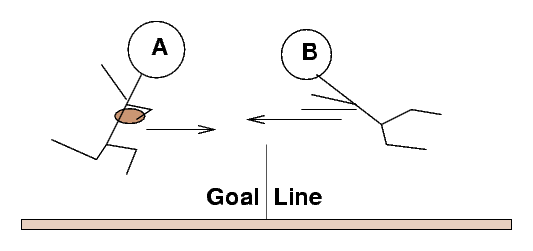
Football players Alex, mA = 100 kg and vA = 5.6 m/s, and Bob, mB = 89 kg, vB = 6.2 m/s collide in mid-air at the peak of their leaps. Bob grabs Alex and prepares to wrestle him to the ground.

1. Is this collision elastic or inelastic?
2. Is energy conserved?
3. Is momentum conserved?
4. What will the velocity of the two players combined be immediately after they collide in mid-air?
5. If they are at a height of h = 30 cm when they meet, how far will they move and in which direction before they hit the ground?
6. Will it be a touchdown?

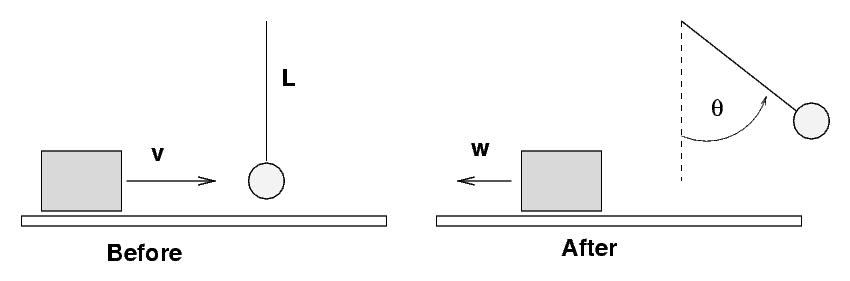
A block of mass M = 4 kg slides at speed v = 5 m/s across a frictionless floor. It collides with a motionless pendulum of length L = 1 m and mass m = 10 kg. The block goes sliding backwards at speed w while the pendulum swings up to a maximum angle theta. The collision is elastic.

It's an easy problem if you know the speed w

1. Is energy conserved?
2. Is momentum conserved?
3. What is the speed of the block immediately after the collision?
4. What is the speed of the pendulum's ball immediately after the collision?
5. What is the angle theta?

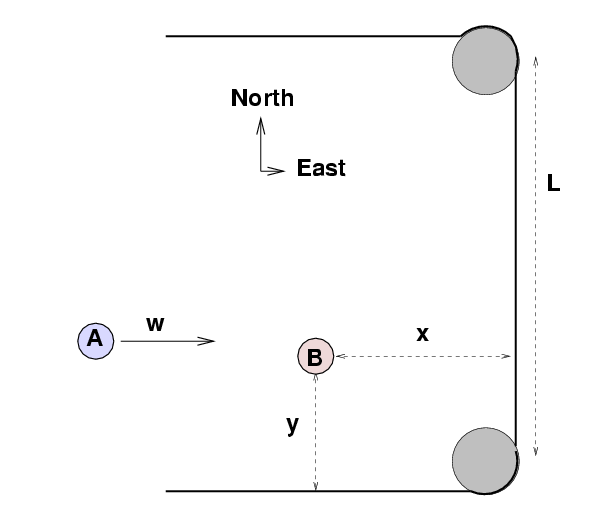
Fast Eddie considers his next pool shot. He needs to strike ball A so that it collides with ball B and sends B into the pocket at the southeastern corner of the table. Ball B is currently a distance x = 43.3 cm and y = 25 cm away from that pocket. Eddie fires ball A at an initial speed of w = 3 m/s; it knocks ball B straight into the pocket and heads off with a final speed z = 1.5 m/s.

1. Was this an elastic collision?
2. The length of the table is L = 1 m. Did ball A fall into the pocket in the northeastern corner?

Copyright © Michael Richmond. This work is licensed under a Creative Commons License.