Complicated collisions: the ballistic pendulum (I)

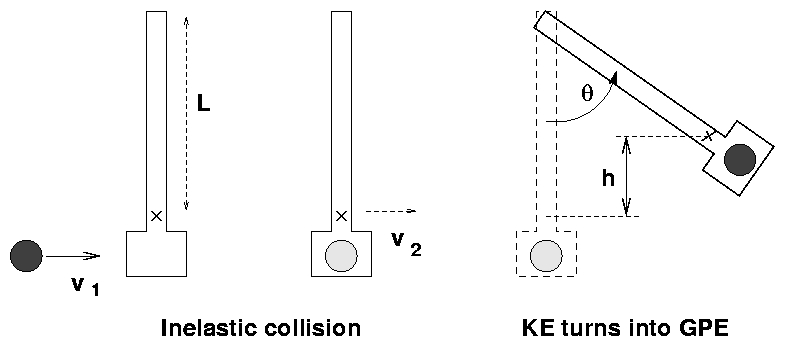
In real life, collisions are often messy affairs which require a mixture of techniques to understand. As an example, consider the ballistic pendulum.

You can break the action into two pieces:

1. A ball of mass m moving at speed v1 slams into an arm of mass M. Use conservation of momentum in this completely inelastic collision to write an equation relating v1 to the velocity of the arm-plus-ball v2.
2. An arm with an initial speed swings up until it halts at an angle theta. Use conservation of energy to figure out the relationship between the speed of the arm-plus-ball v2, the angle theta, and the height h by which the center of mass of arm-plus-ball rises.

Your first job today is to figure out the speed v1 with which the ball is fired from the catapult, by measuring the angle theta (and some other quantities).

• be very gentle with the swinging arm
• use the stuffing rods to push the ball into the catapult
• make 3 measurements for each of the three positions of the spring-loaded gun: short-range, medium-range, and long-range
• you will need to find the position of the center of mass of the arm-plus-ball
• watch the device when you fire the catapult. If it slides across the table, your measurements will be inaccurate: some of the momentum goes into the motion of the whole device, which you cannot measure
• try to estimate the uncertainty in each of the four quantities you need to measure

You should end up with one table showing all your measurements, and the uncertainty associated with each measurement. You should also have a value of v1 for each of the three range settings: short, medium and long.

Bonus! Compute the uncertainty in v1 for each of the three settings.

As you try to convert the uncertainties in the values you measured in class into an uncertainty in the initial speed v1 of the ball, you may find it useful to peruse

• this GENERAL guide to using uncertainties in calculations
• this SPECIFIC example of using uncertainties in the ballistic pendulum; the numbers will be different than yours, but the method should be the same
  • Part 1 of example
  • Part 2 of example
  • Part 3 of example

Your second job is to calculate the spring constant k of the spring in the gun in two ways.

1. Energy-based measurement

Use your measurements of the initial speed of the ball to compute the kinetic energy of the ball. Assume that this kinetic energy (KE) is exactly the same as the spring potential energy (SPE) stored in the compressed spring. Measure the distance -- and uncertainty -- by which the spring is compressed for each of the three range positions: short, medium, and long. Compute the spring constant using data for each range position individually. Do all three values agree?

Bonus: Compute the uncertainty in each value for the spring constant, using uncertainty in KE and uncertainty in distance compressed. Do the three values agree within the uncertainties?

2. Force-based measurement

Figure out a way to compress and hold the spring at some position using a known force. Use that force, and the amount by which the spring is compressed, to compute the spring constant.

Bonus: Use uncertainties in the force and displacement to compute an uncertainty in this force constant.

Compare the two force constants. In an ideal world, they would agree within their uncertainties. Do they? If not, try to explain why not. Be specific and quantitative.

Which of the two methods do you think is more reliable? Why?

Copyright © Michael Richmond. This work is licensed under a Creative Commons License.