 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
The ballistic pendulum
A ballistic pendulum takes the horizontal motion of a ball
and turns it into the swinging arc of an arm around
a pivot:
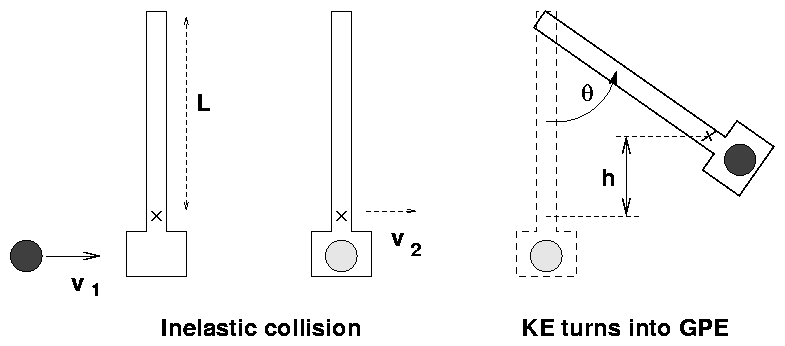
You can break the action into two pieces:
- A ball of mass m moving at speed v1 slams
into an arm of mass M. Use conservation of
momentum in this completely inelastic collision
to write an equation relating v1 to the velocity
of the arm-plus-ball v2.
- An arm with an initial speed swings up until it halts
at an angle theta.
Use conservation of energy to figure out the relationship
between the speed of the arm-plus-ball, the angle theta,
and the height h by which the center of mass of
arm-plus-ball rises.
Your job today is to figure out the speed v1 with which the
ball is fired from the catapult, by measuring the angle theta
(and some other quantities).
- be very gentle with the swinging arm
- use the stuffing rods to push the ball into the catapult
- cock the catapult to the middle position -- two clicks. Do NOT
go all the way to three clicks
- you will need to find the position of the center of mass
of the arm-plus-ball
- watch the device when you fire the catapult. If it slides
across the table, your measurements will be inaccurate:
some of the momentum goes into the motion of the whole
device, which you cannot measure
- try to estimate the uncertainty in each of the four
quantities you need to measure
As you try to convert the uncertainties in the values you
measured in class into an uncertainty in the initial
speed v1 of the ball,
you may find it useful to peruse
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.

 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.

 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.