 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Scientists often take a census of items: stars in the solar neighborhood, or insects in the forest, or subatomic particles in a region of space. When one counts items and measures their properties, it is often useful to create a distribution, showing the number of items with some particular property.
For example, suppose that Joe Astro studies the stars in three different clusters. He measures the mass and luminosity of each star in each cluster. Here are his counts:
How can Joe count fractional stars? His eyepieces need to be cleaned, apparently
# Mass Number of stars with that mass
# (solar) A B C
#------------------------------------------
0.3000 746.30 50.00 5.46
0.8000 67.85 50.00 18.12
1.3000 35.54 50.00 25.04
1.8000 24.07 50.00 30.42
2.3000 18.20 50.00 34.99
2.8000 14.63 50.00 39.02
3.3000 12.23 50.00 42.67
3.8000 10.51 50.00 46.04
4.3000 9.21 50.00 49.17
4.8000 8.20 50.00 52.12
5.3000 7.39 50.00 54.91
5.8000 6.72 50.00 57.57
6.3000 6.17 50.00 60.10
6.8000 5.70 50.00 62.54
7.3000 5.29 50.00 64.88
7.8000 4.94 50.00 67.14
8.3000 4.64 50.00 69.33
8.8000 4.36 50.00 71.45
9.3000 4.12 50.00 73.51
9.8000 3.91 50.00 75.51
#------------------------------------------
It's clear that the properties of stars in these clusters are quite distinct:
Is there a way to put these statements into some sort of mathematical form? In other words, can we come up with some sort of formula which explains how likely it is to find a star of some particular mass in each cluster?
Yes!
One type of mathematical form which is very useful is called the power law. It's very useful for three reasons:
Joe decides to write a power law describing the distribution of stars as a function of mass like so:
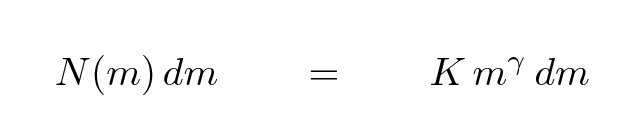
Notice the middle section of the right-hand side: it involves one quantity (mass, in this case) raised to some power (γ, in this case). That's why this sort of equation is called a power law. Let's look at each piece of the equation.
It's important to remember that whenever we try to use the equation, we need to specify some range over which we'll count. Look at the start of Joe's table, for example:
# Mass Number of stars with that mass
# (solar) A B C
#------------------------------------------
0.3000 746.30 50.00 5.46
0.8000 67.85 50.00 18.12
1.3000 35.54 50.00 25.04
1.8000 24.07 50.00 30.42
... ... ... ...
#------------------------------------------
There are 35 stars in cluster A with a mass of about 1.3 solar masses, right? A more precise statement is that, Joe counted 35 stars in cluster A which had masses in the range between 1.05 and 1.55 stellar masses, We might say, "Joe counted 35 stars in a bin of width 0.50 solar masses, centered on 1.30 solar masses." If we don't include the range (or bin width) in our statement, then our statement is meaningless. After all, Joe counted 127 stars with a mass of about 1.3 solar masses -- if you use a range from 0.55 to 1.95.
Sticklers for clarity might write the power law in a slightly different manner:
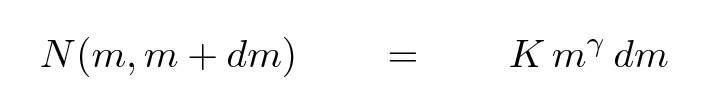
There's no ambiguity here: the equation yields the number of stars with masses in the range from m to m + dm.
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.