Good old local time
Local time is the time we use in ordinary life. For example, this class is scheduled to meet four days a week at 1:00 PM local time.
Local time is designed to follow the Sun. The goal is to arrange our clocks so that the Sun rises around 6 AM, reaches its peak around noon, and sets around 6 PM. It's convenient from a practical point of view: if you are travelling to a foreign country and know that your plane will arrive at 23:00 local time, then you know most people will probably be at home and sleeping when you touch down. You'll probably have to call a cab ...
One annoying feature of local time is that (in most states of the US) it shifts by one hour twice a year. During Daylight Savings Time, which starts April 3 this year, clocks are shifted forward one hour: what used to be 7 AM is now 8 AM. Sometime in the autumn (this year on October 30), clocks are shifted back one hour to Standard Time.
This shift can make it difficult to calculate the interval between two events, if they span the start or end of Daylight Savings Time.
Universal Time
When people living in different parts of the world want to coordinate their actions, the differences between time zones become a big hassle.
Q: What is the current difference between the time in Rochester, NY, and Timbuktu, Mali?
Therefore, people decided long ago to make one time zone "special" and use it for a worldwide standard. Just as the longitude system is centered on Greenwich, England, so the time system is as well. There are several names given to the time at Greenwich (see notes below for names with asterisks *)
- Greenwich Time, or Greenwich Mean Time (GMT)
- Zulu Time (a military designation)
- Universal Time (*)
- Coordinate Universal Time (UTC) (*)
(*) There are actually small differences between several varieties of Universal-ish time. For our purposes, they may be treated the same, but if you are interested in accuracy at the sub-second level, you'll need to know the differences. See the references at the end of today's lecture.
Astronomers typically use Universal Time to refer to events. Look, for example, at the listing of asteroid occultations visible in March:
Universal Time (at least some varieties)
and local time (all varieties)
are tied to the Earth's rotation.
For many purposes, that's fine:
the Earth rotates at a nearly constant rate.
But over the course of a decade, small changes
in the Earth's rotation rate can cause
a significant difference to build up between
a perfect clock and the location of the Sun.
...
These very small drifts between the Earth's rotation
and the ticking of a perfect clock
lead to
leap seconds:
extra seconds which are added (or subtracted)
from the official civil time
to keep the civil clocks in line with the Earth's rotation
(and, hence, with the Sun).
Leap seconds can be a nuisance if you
are trying to calculate the exact interval
between two events many years apart.
A list of all leap seconds and the answer
To avoid the complications of leap seconds,
scientists have devised
a time system based on clocks
which are more consistent than the Earth's rotation.
International Atomic Time (TAI)
is defined by the action of a set of atomic clocks.
You can find tables which tell the difference
between Universal Time and TAI over a range of dates.
The Global Positioning System (GPS) satellites
use something like TAI:
a system which runs more precisely than the Earth's rotation,
and does not include leap seconds.
Suppose that there is a distant celestial source
which undergoes some regular variation:
for example, an eclipsing binary star which has a
period of exactly 5 hours.
By a nice coincidence, today the Earth
happens to be at the point in its orbit
which is closest to this distant binary star.
Measurements made last night indicate
that the next set of eclipses will occur at
these times:
And ... they do occur at these times. Good!
But over the course of several months, the Earth will move
around the Sun in its orbit.
About two months later,
the Earth will be located here:
When we observe the binary star from this location,
we see that the eclipses are occurring a little bit later
than predicted:
So, if one monitors a celestial source over the
course of one year, one will see small variations
in the time of (what should be) regular events.
The small variations accumulate over the course of
an entire year to impressive amounts:
the time it takes light to travel across the
distance of the Earth's orbit, from one side
of the Sun to the other, is ...
In order to avoid variations in the timing of celestial
events due to the Earth's motion around the Sun,
astronomers sometimes use
a time system called
barycentric or "heliocentric".
Basically, one calculates when the event would have been
seen by an observing sitting at the position
of the Sun,
and thus avoids the extra time required for the signal
to reach the Earth in its orbit.
Because the Sun doesn't sit perfectly still, but
does move in a very small orbit due to the gravitational
pull of the planets (mostly Jupiter),
the best choice is
barycentric.
The official abbreviation is
TDB, which stands for Barycentric Dynamical Time.
Using barycentric time is not always necessary.
It does appear frequently in the timing
of eclipses of binary stars:
scientists searching for changes of just a few seconds
in the period of a binary star's orbit
(which may reveal properties of the interior stellar structure)
must avoid any systematic errors which are minutes in size.
The first few are easy, but as one considers longer
and longer stretches of time,
another complication appears:
leap days.
Leap days are extra days inserted into the modern
calendar as February 29.
We need these extra days to keep the calendar
in sync with the Sun.
The problem is that the Earth takes
about 365 and a quarter days
to orbit the Sun.
If we simply count 365 days as one year,
then the calendar will start running ahead
of the Sun:
the shortest day of the year might
be Dec 21 in 2005, but then Dec 22 in 2009,
Dec 23 in 2013, and so on.
After a century, the
shortest day of the year would move to roughly
January 15!
Therefore, we insert one extra day roughly
every four years.
Actually, the rule is
Astronomers quickly tired of the extra
work required to count the number of days between
any two given calendar dates.
Back in the sixteenth century,
Joseph Scaliger devised a scheme to make
the calculations easier:
he picked a particular date,
long, long ago (see references below for his choice),
and started counting days from that point forward.
His starting point was:
Scaliger named his system
after his father,
Julius Caesar Scaliger.
We call dates in this system
Julian Dates, or JD for short.
There are many calculators on the web for converting
to and from Julian Date.
Now
(2012 March 13 at 9:20 AM Eastern Daylight Time)
is Julian Date
2,456,000.0555.
It gets a bit awkward to keep typing all those digits,
and hard to keep track of them all,
so astronomers frequently subtract away a big
round number. For example,
This sort of modification is handy when plotting light curves
of variable stars, since otherwise the labels on the time
axis can be so long that they run into each other.
If you ever decide to cut off a portion of the long
JD number, please be explicit about exactly what
you are subtracting.
Finally, there is one time system
which is designed specifically for observers
out in the field.
Local Sidereal Time (or LST for short),
like civil time or Universal Time,
is based on the Earth's rotation;
but, unlike them, it does not account
for the Earth's orbital motion around
the Sun.
The Earth takes about 23 hours and 56 minutes
to rotate once around its axis.
That means that if you go outside and watch
the motion of one particular star,
there will be 23 hours and 56 minutes
between successive star-rises or successive star-sets.
Because the Earth moves a small distance around
the Sun its orbit, the Sun takes an additional
4 minutes to "catch up" to the Earth:
there are 24 hours between successive sunrises
or successive sunsets.
This introduces a gradual shift in the positions of stars
from night to night
(click on the image to see the nightly shift over the
course of one week).
The shift is obvious if we skip ahead by 30 days at a
time. You've undoubtedly noticed that stars visible
early in the evening during one month aren't visible
at the same time several months later.
Local Sidereal Time (LST)
treats the stars in your sky like a big clock:
the LST is equal to the Right Ascension of the
stars which are currently overhead (or as high in the sky as they get).
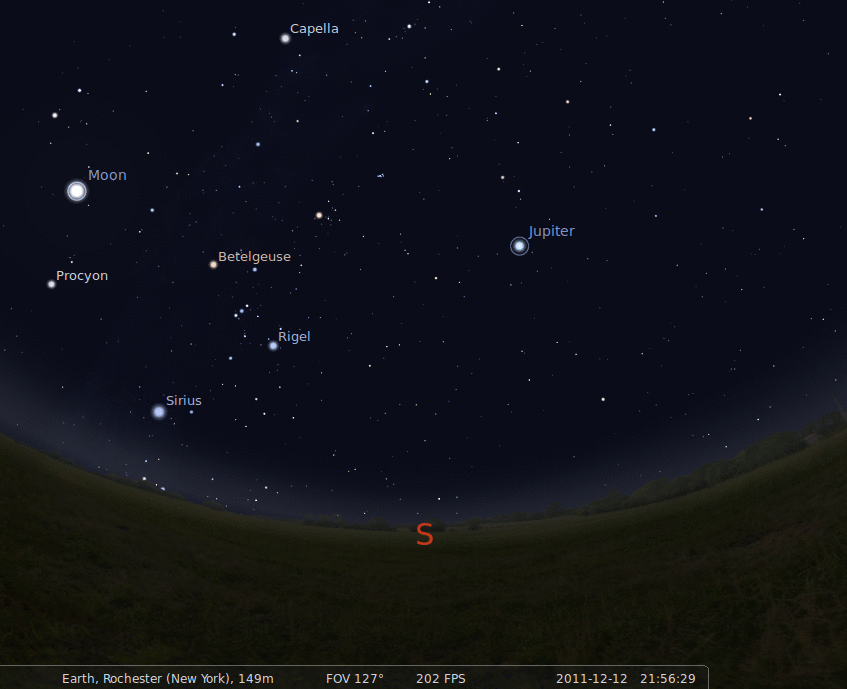
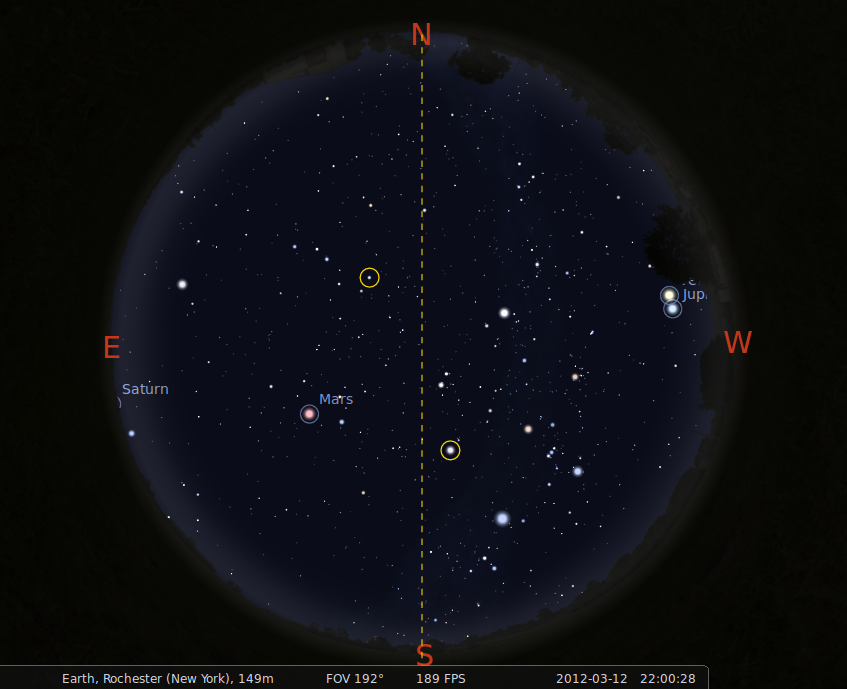
Tonight, for example, at 10:00 PM,
the sky will look like this:
Note that Procyon, at RA = 07:39, is slightly to the
west of the meridian (the line running North-South through overhead);
that means that the LST is later than 07:39.
On the other hand, Dubhe, at RA = 11:03, is still rising up
from the East, so the LST must be earlier than 11:03.
Let's focus on the stars in the southern part of the sky tonight.
What is the LST when the sky looks like this?
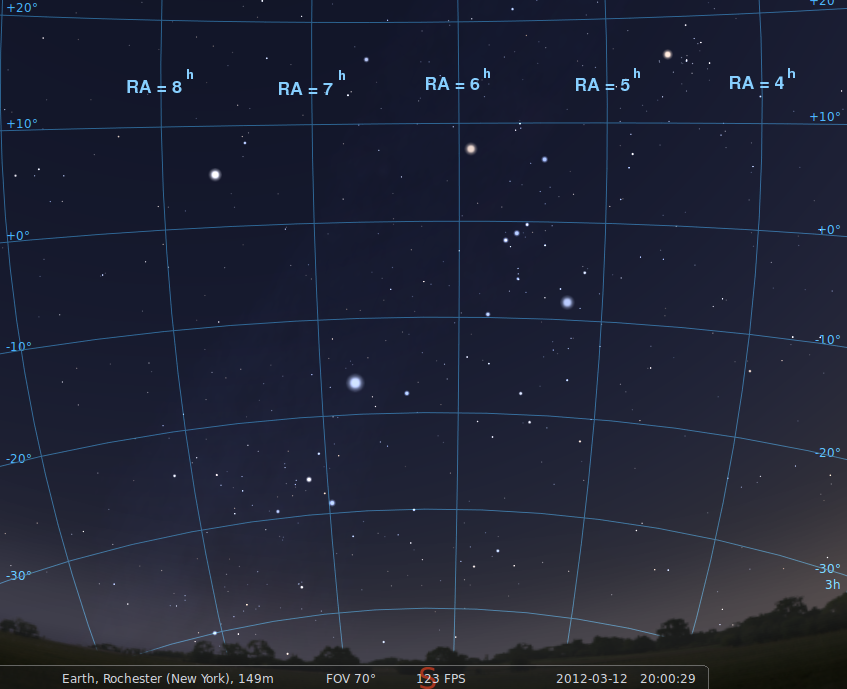
One hour later, the sky looks like this.
What is the LST now?
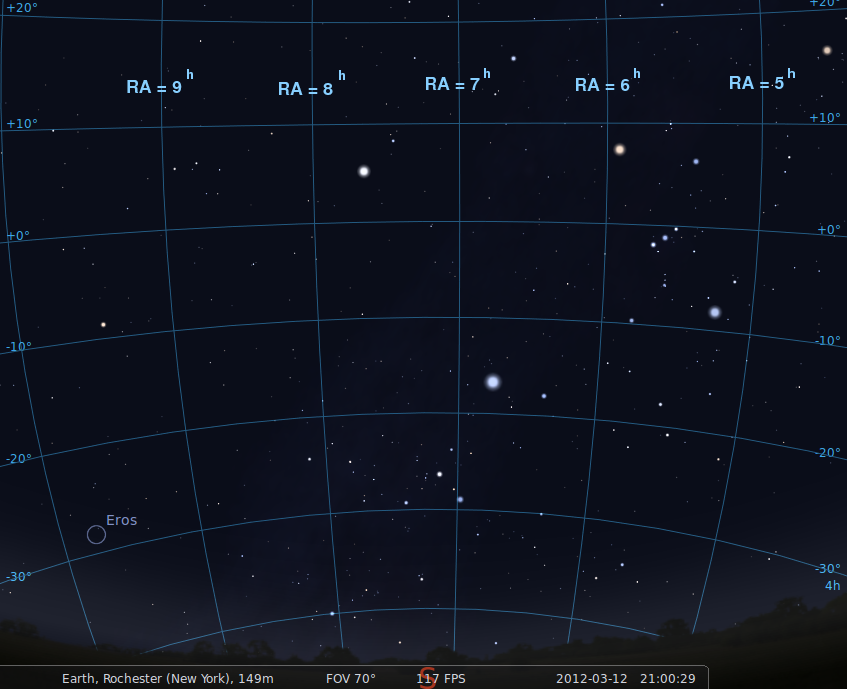
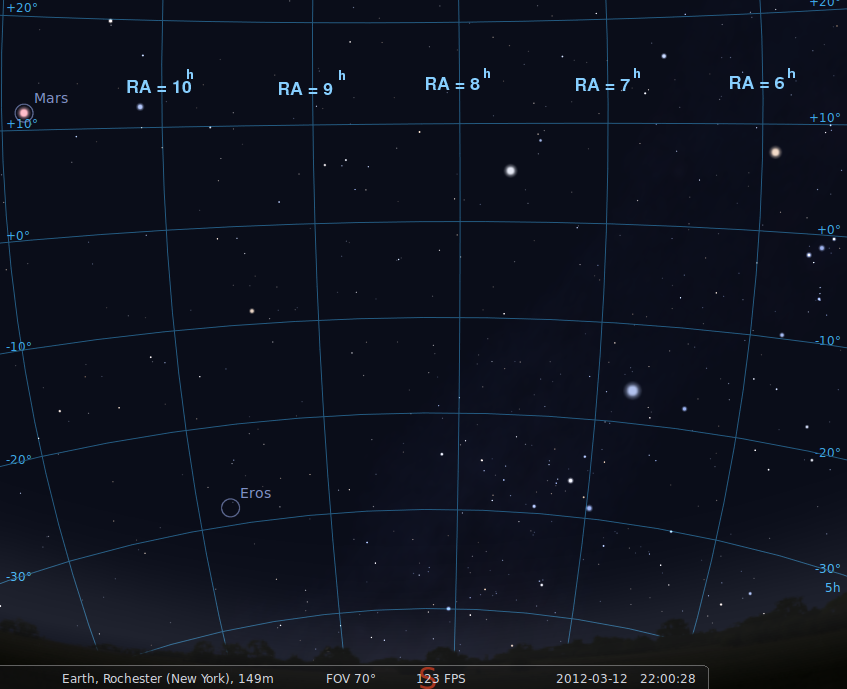
One hour later, the sky looks like this.
What is the LST now?
Last modified by MWR 3/8/2005
Atomic Time
Q: What is the time interval between events A and B?
Barycentric (or heliocentric) time
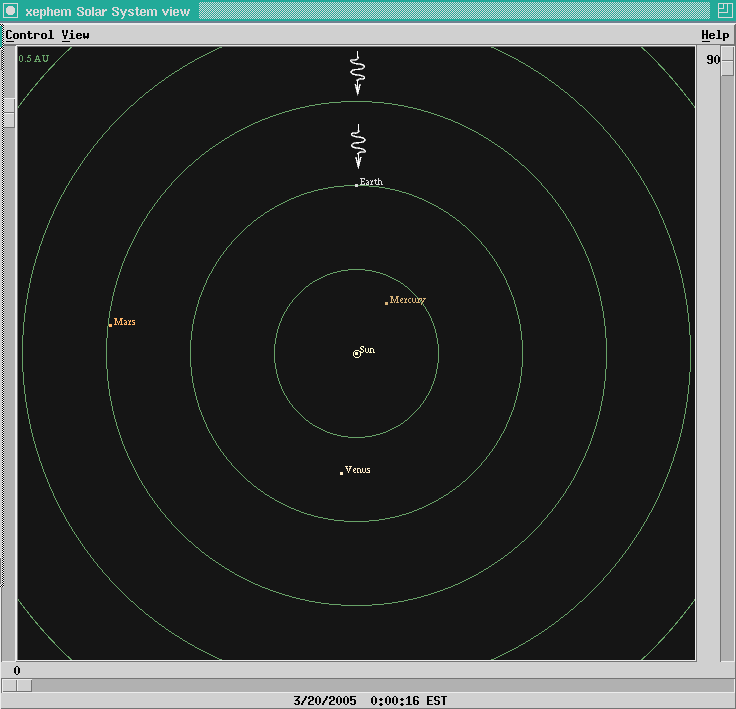
1:37 6:37 11:37 16:37 21:37 ....
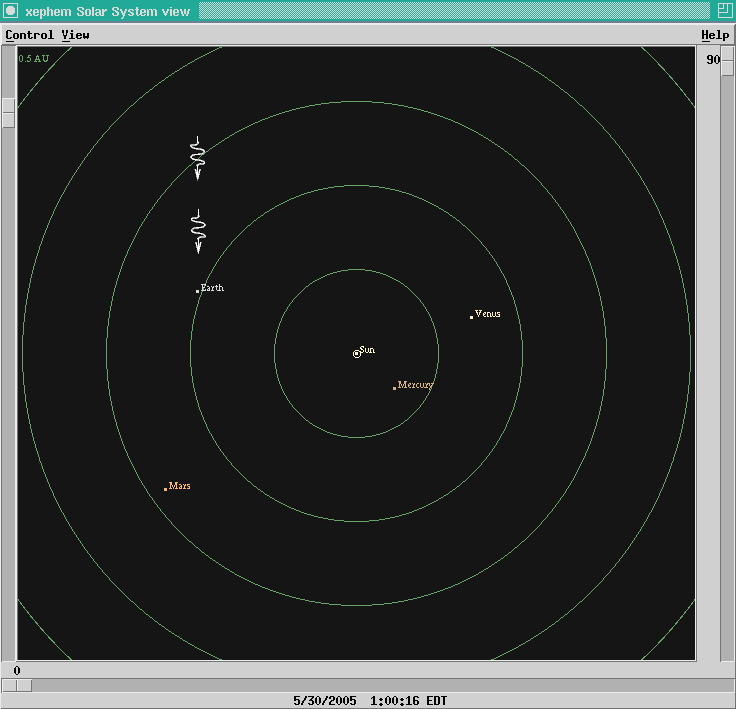
predicted: 1:37 6:37 11:37 16:37 21:37 ....
observed: 1:42 6:42 11:42 16:42 21:42 ....
Q: Why are the eclipses not happening at the
predicted time?
Q: Will one always see these variations,
for all sources in the sky?
Q: How long does it take light to travel
across the diameter of the Earth's orbit?
Julian Date
Can you answer the following questions?
JD 2453437.2778 turns into 437.2778 (for JD - 2,453,000)
Local Sidereal Time
Homework
Answers
(Hint: consider using Julian Dates ....)
For more information
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.