Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
It's bad enough that there are several different coordinate systems used by astronomers. But what's even worse is that, even when you have chosen one coordinate system, the coordinates of stars in that system will change over time. Fortunately, these changes are usually very slow, acting over decades or centuries, but you must be aware of them to compare accurately measurements made in the nineteen-fifties to measurements made today.
After discussing the two major reasons for changes in stellar positions, I'll show you how to calculate the angular distance between two locations on the sky. Most planetarium programs will do this for you, but it never hurts to know what's going on inside the box.
Let's watch the stars as they glide through the sky
over the course of a night:
The constellations appear to circle around the Pole Star,
Polaris, at the end of the Little Dipper's handle.
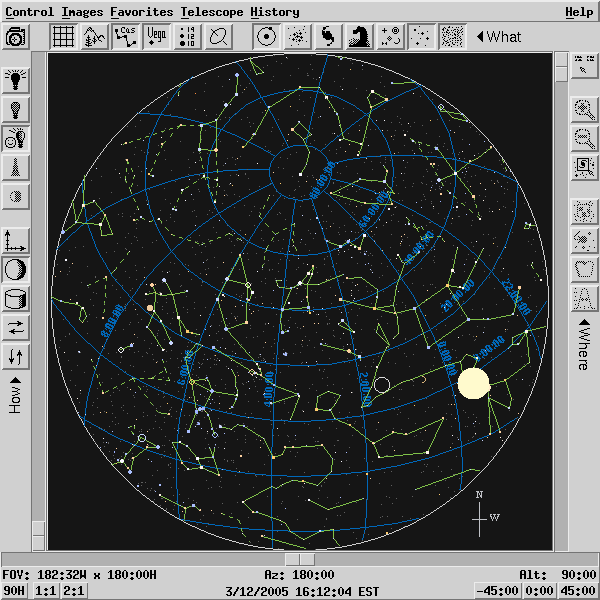
Over the course of any single human lifetime,
that's the way it goes.
But what would happen if we could watch the sky
night after night for centuries?
For example, let's jump forward in time
one thousand years, to March 12, 3005,
and once again watch the Rochester skies after sunset.
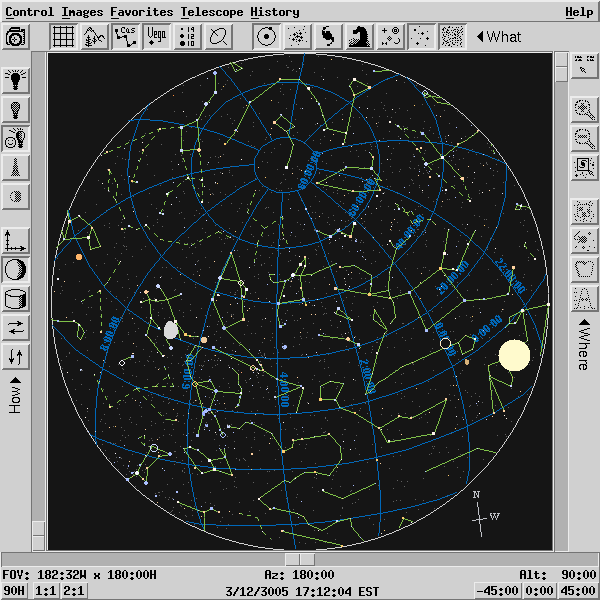
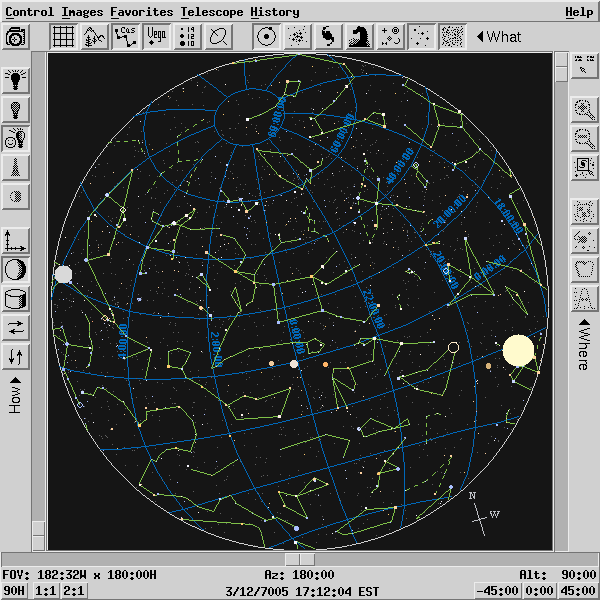
Let's jump forward even farther, to the year 7005,
a round five millenia into the future.
The reason for the change in the apparent motion of the stars
has nothing to do with the stars themselves;
instead, it's all due to the Earth.
As the Earth spins around its axis,
it feels gentle gravitational tugs (torques)
due to the Moon and to the Sun.
In very simple terms, the torques are caused by
the differential gravitational force exerted on the near
and far sides of the Earth's equatorial bulge:
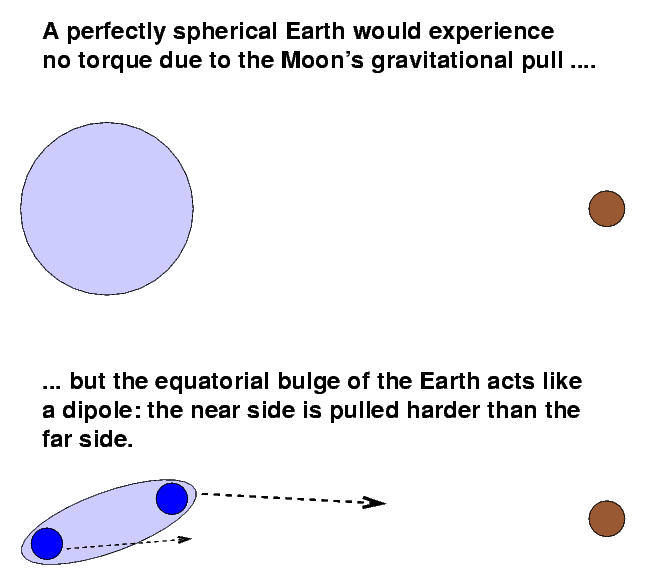
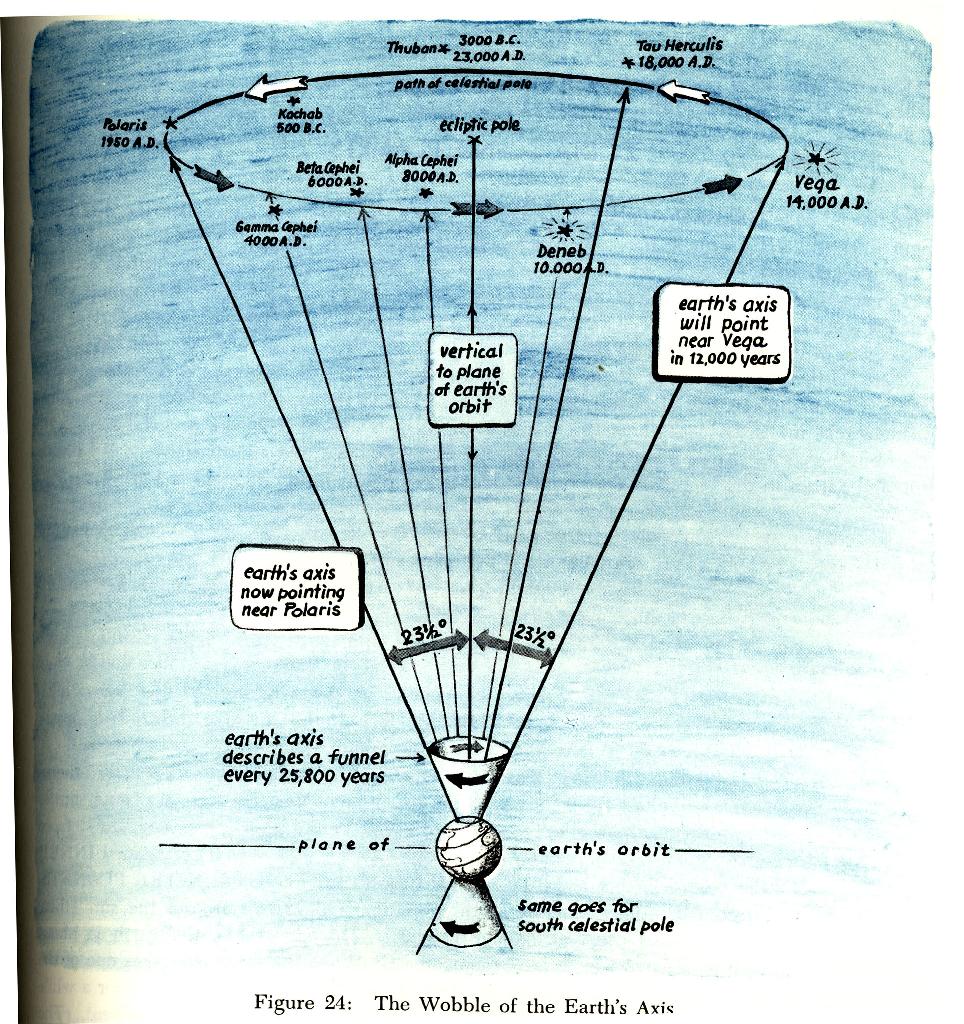
The torque causes the spinning Earth to
precess: its axis of rotation slowly
rotates. It takes about 26,000 years to make one
complete cycle.
This illustration from
H. A. Rey's book
The Stars: A New Way to See Them
illustrates the change in the "pole star"
over the period of the precession of the equinoxes.
Astronomers want their (RA, Dec) coordinate system
to be aligned with the Earth's axis of rotation ...
so as the Earth precesses, astronomers
move their coordinate system to follow it.
That means that the (RA, Dec) coordinates will slowly
drift across the background of stars.
Look at the Pleiades over the period 1950 to 2000:
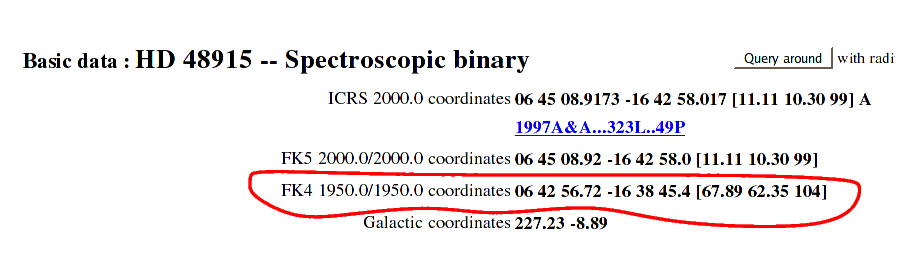
It's a big pain to re-publish the coordinates
of all the stars and galaxies, so
astronomers only do it occasionally.
There was one big set of catalogs produced
for the direction of the Earth's axis in 1950;
those coordinates are referred to as
(1950) or (B1950) or "equinox 1950".
Another big set of catalogs was created fifty years
later, using the direction of the Earth's axis in
the year 2000. These are denoted by (2000) or (J2000)
or "equinox 2000".
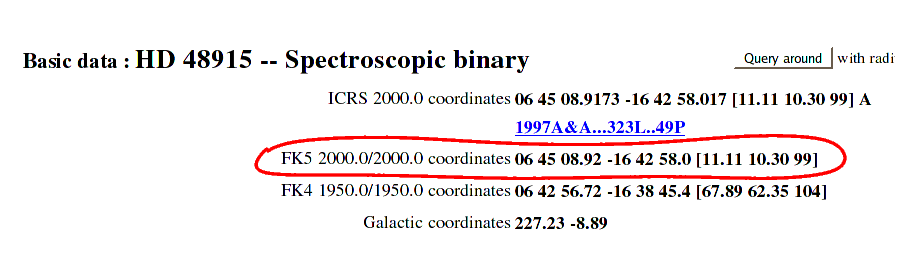
For our purposes, the "equinox 2000" positions
are preferred.
Please use them unless directed otherwise.
You can find tools to convert coordinates
from one equinox to another in many places --
most planetarium programs will do it, for example.
You may have to prepend the letter "B"
to an equinox when you type them into a
converter -- so that you refer to a star with coordinates
of equinox 1923 as having equinox B1923.
Suppose that we just take a picture of the
stars, like this one of the Big Dipper:
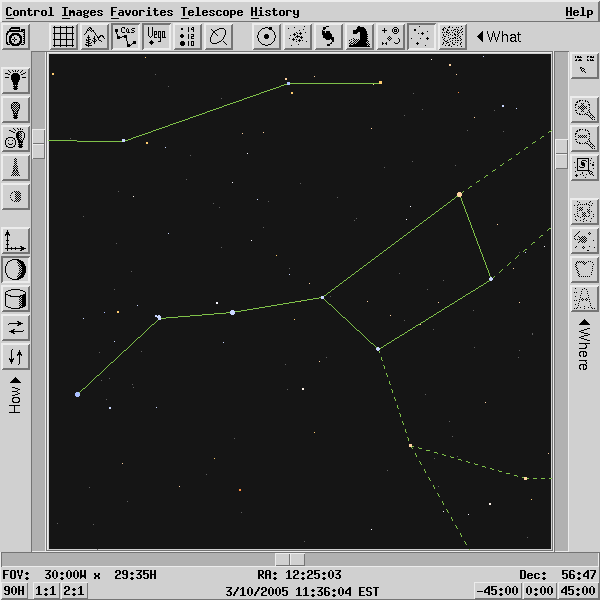
If all we care about is the relative positions
of the stars -- which create the shapes of the
constellations --
then we can ignore precession;
precession only changes the coordinates assigned
to the stars, not their relative positions.
So, we might expect the Big Dipper to remain
unchanged in the sky as the years go by ...
but is it really?
Let's step into the Wayforward Machine
and set the dial for steps of 1000 years:
Hey! The stars are all wandering away from their
original positions!
The effect is even more obvious if you
look at
a movie of Ursa Major from 100,000 BC to 100,000 AD ;
thanks very much to
Richard Pogge at Ohio State University
for making this available.
You might also run your own simulations with
Tony Dunn's proper motion simulator (runs in a browser).
Astronomers call this very gradual
glide across the sky the
proper motion of a star.
It depends on two factors:
Over the past few hundred years,
astronomers have carefully measured the proper motions
of thousands of stars.
The values
are often expressed in units of
"arcseconds per year," or sometimes "milliarcseconds per year."
In the example below, there are two values given:
Hmmmm.
Does this mean we can just add 3.1 arcseconds
to the RA value for the star in example above?
How would that work?
That brings up the whole topic
of the arithmetic of angular distances.
Doing geometry on a plane is easy:
you learned the rules in high school.
If you want to know the distance between two points ...
Astronomers, however, don't deal with objects
sitting on a plane.
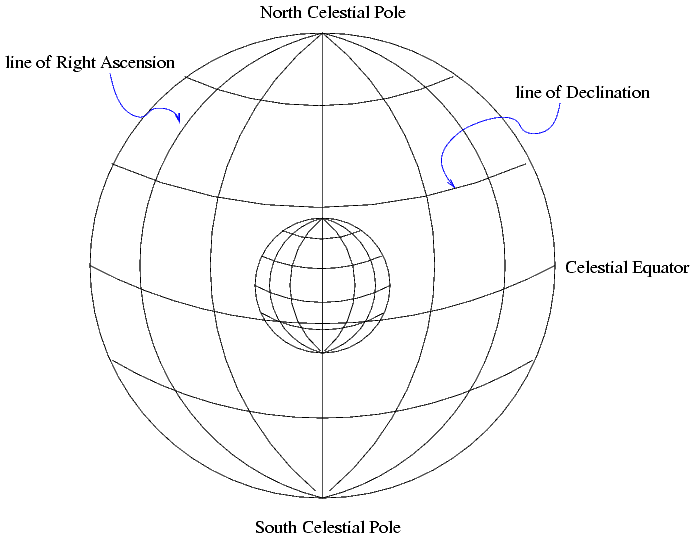
From our point of view on Earth,
stars and planets appear to be projected
onto a SPHERE surrounding the Earth.
The coordinate systems we use,
such as the equatorial (RA and Dec) or galactic (galactic latitude
and longitude), all involve
positions on this celestial sphere.
Geometry on a sphere does NOT follow the same
rules as geometry on a plane.
For example,
In order to determine the distances between objects
on the celestial sphere, we need to use
spherical trigonometry.
There are entire books devoted to this rather arcane
subject, such as
I will provide here just a few of the most basic rules.
First, note that angles which run purely North-South
are easy to understand:
So calculating arclengths between two positions which
differ only in Dec is easy.
For example,
But angles which run parallel to the equator
of the coordinate system are more complicated....
The arclength of a circle which is parallel
to the celestial equator
changes with Declination:
One can calculate the arclength of an angle between
two points which have the same Dec by correcting
for this factor:
For example, if two stars have the same Declination,
and differ only in RA,
If two points are very close together on the sky --
within a degree or less --
than one can calculate approximately the distance
between them by adding this little correction factor
to the Pythagorean formula.
Make sure that both RA and Dec are expressed in
decimal degrees, and then compute
But for the general case of two locations
separated by an arbitrary distance,
one must fall back upon the full
formula
to calculate the arclength γ
between the two locations.
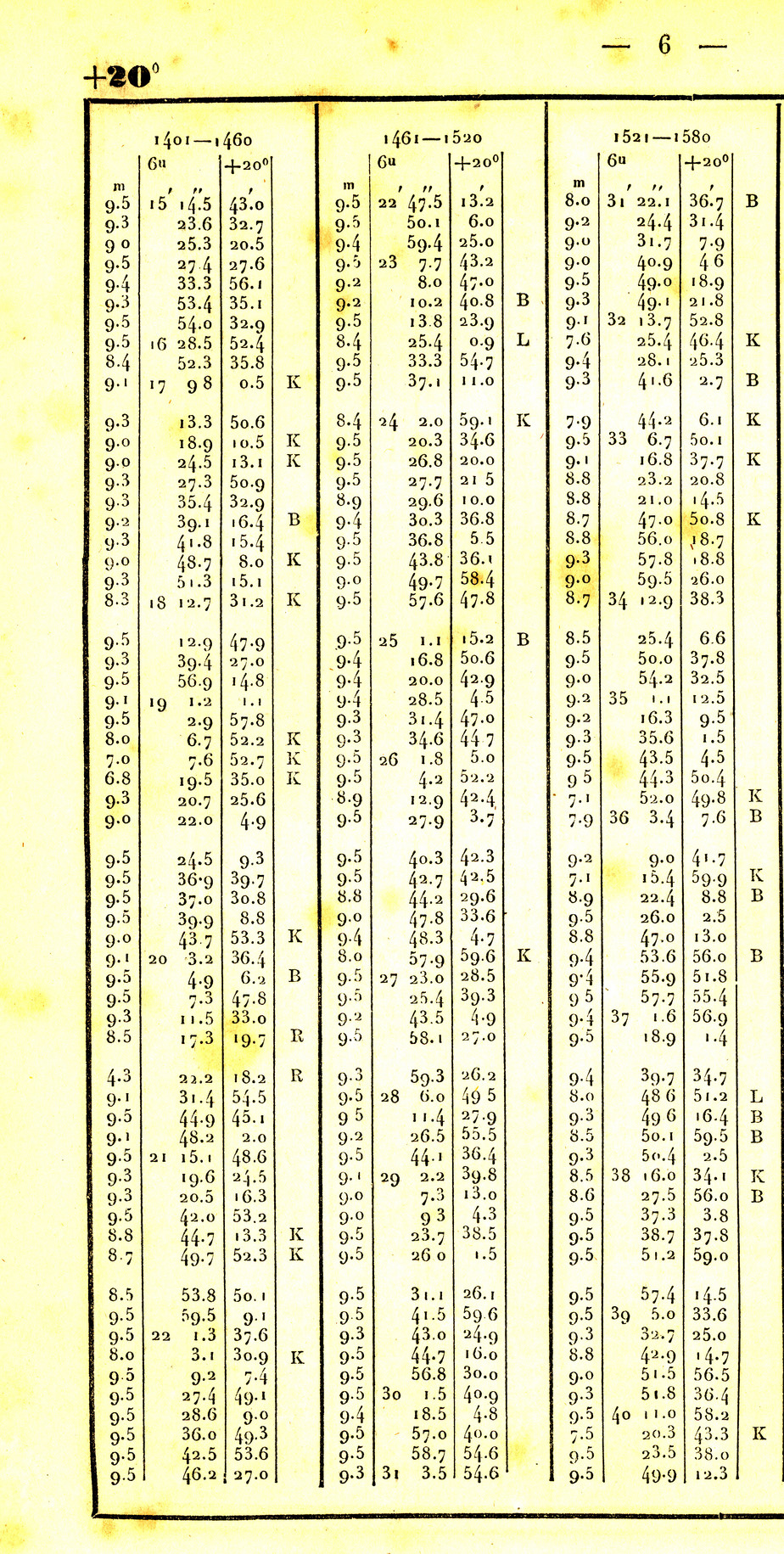
The top of the page shows that stars on this page
belong to zone +20; that means they are all
in a strip around the sky near Declination = +20 degrees.
Below that is one column from the page: it shows
the list of stars numbered 1401 to 1460 in the zone +20:
the first star is called BD +20 1401, the
second star BD +20 1402, and so forth.
The leftmost number is the magnitude of the star --
small numbers mean bright stars, big numbers mean faint
stars (we'll discuss magnitudes later).
The middle numbers give the Right Ascension of the star.
All the stars on this page fall into RA = 6 hours;
the numbers below show the minutes and seconds of RA.
The right-most numbers provide the declination of the
star: all have Dec = +20, but the minutes and fractions
of a minute are listed for each star.
Thus, the second star in the list has
Look at the stars on this page of the catalog (click on the
image for a larger version):
(This is the hard part -- just do your best)
Last modified by MWR 3/10/2005
Precession
Q: Why do the stars appear to rotate around this point?
Q: What is the (RA, Dec) position of the North Celestial Pole?
Q: How do the stars and constellations move now?
Q: What happens now?
Q: What is going on???
The Stars: A New Way to See Them by H. A. Rey,
published by Houghton Mifflin (1976) -- it's my FAVORITE constellation book!
Proper Motion
Q: Why are the stars moving individually in
different directions?
Q: How far in RA should Aldebaran move in 50 years?
How far in Dec should Aldebaran move in 50 years?
Calculating the angular separation between objects
etc.
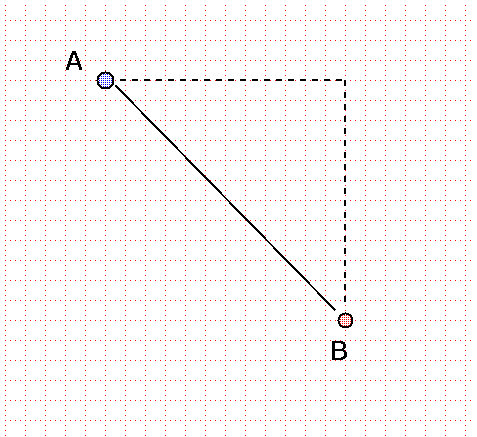
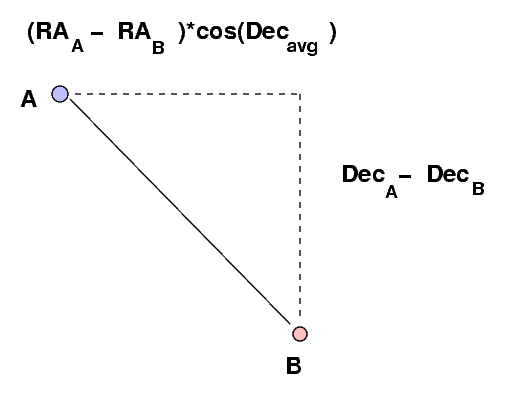
Q: How do you find the distance between points
A and B in the figure above?
etc.
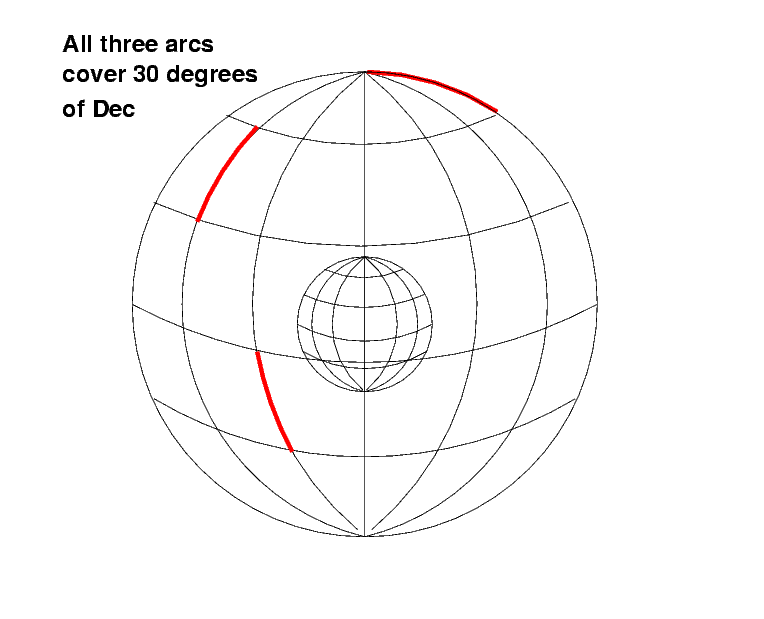
Q: Are all three red arcs the same length?
A has Dec = +30:23:34 = 30.3928 degrees
B Dec = +30:18:12 = 30.3033 degrees
delta Dec = (30.3928 deg - 30.3033 deg)
= 0.0894 deg
= 00:05:22
= 0 degrees, 5 arcminutes, 22 arcseconds
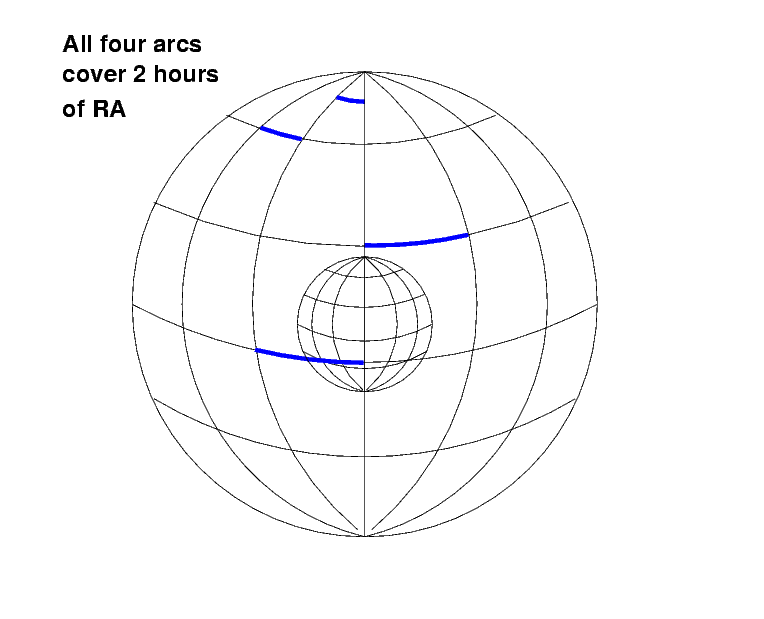
Q: Are all four blue arcs the same length?
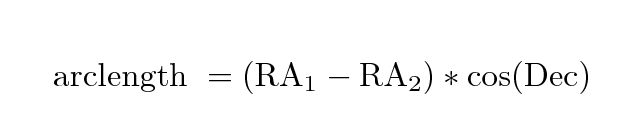
A has RA = 02:33:48.7 and Dec = +20:00:00
B RA = 02:02:31.3 and Dec = +20:00:00
First, convert the RA to decimal degrees in two steps,
for both stars.
A RA = 02 hours 33 minutes 48.7 seconds
= 2 hours + (33/60) hours + (48.7/3600) hours
= 2.5635 hours
There are 24 hours of RA around the sky, which equal
360 degrees of RA. So each hour of RA must equal 15 degrees.
A RA = (2.5635 hours) * (15 degrees/hour of RA)
= 38.4529 degrees
B RA = 02 hours 02 minutes 31.3 seconds
= 2.0420 hours
= 30.6304 degrees
Now, calculate the difference in RA, including the correction
factor based on the Declination.
delta RA = (38.4529 deg - 30.6403 deg) * cos(20.0000)
= (7.8122 deg) * (0.9397)
= 7.3411 deg
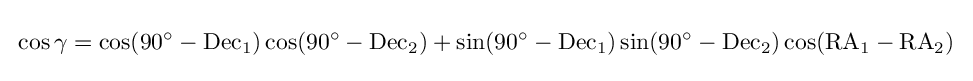
Homework
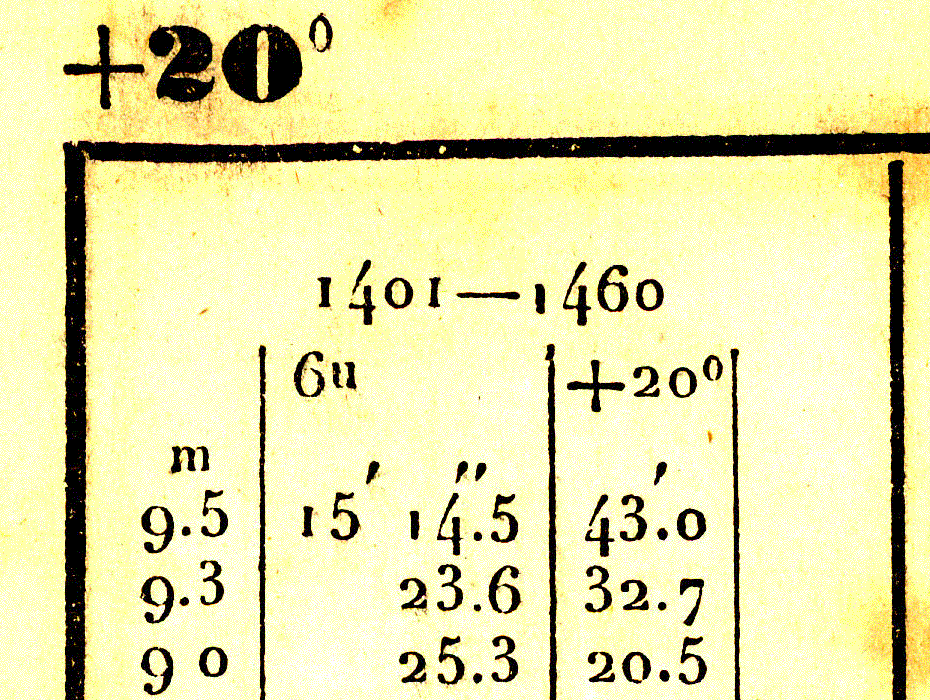
Why does the catalog have this somewhat confusing,
very abbreviated format? Think about it for a moment.
The entire catalog runs to eight (I think) volumes
each over three hundred pages long!
For more information
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.