Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
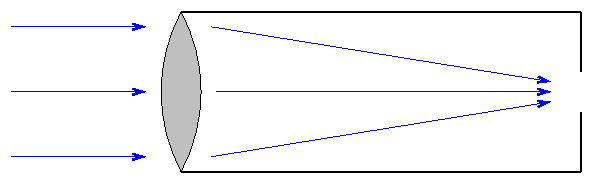
The earliest telescopes -- like the ones Galileo used -- are the simplest: we call them refractors. They consist of a long, narrow tube with a lens at the front end. Light which passes through the lens is bent, so that initially parallel rays meet near the bottom of the tube.
Refractors are easy to make and, when small, relatively inexpensive. Large telescopes of this sort become unwieldy. The largest refractor ever put to practical use is the Yerkes 40-inch instrument; its aperture (front lens) is 40 inches in diameter. The tube is a bit longer ...
There are several drawbacks to this design:
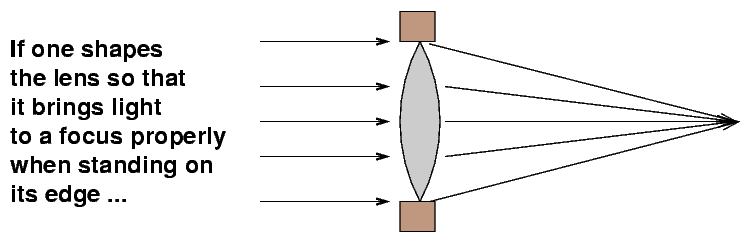
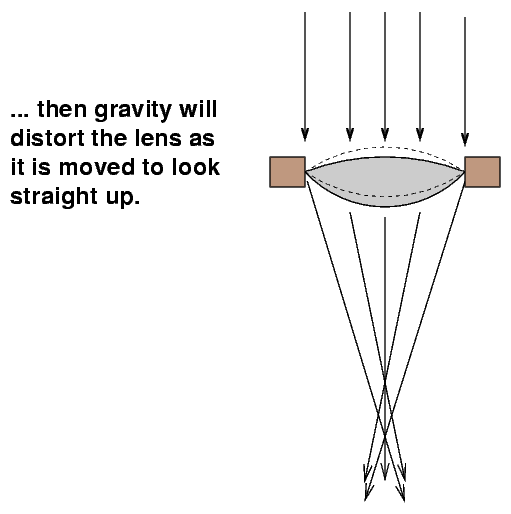
The largest refracting telescope ever built had a lens of diameter 1.25 meters. It was fixed in place to avoid sagging, pointed horizontally at a flat mirror; the flat mirror was tilted to change the part of the sky viewed by the big telescope. It still didn't work....
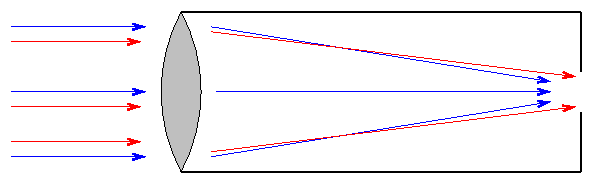
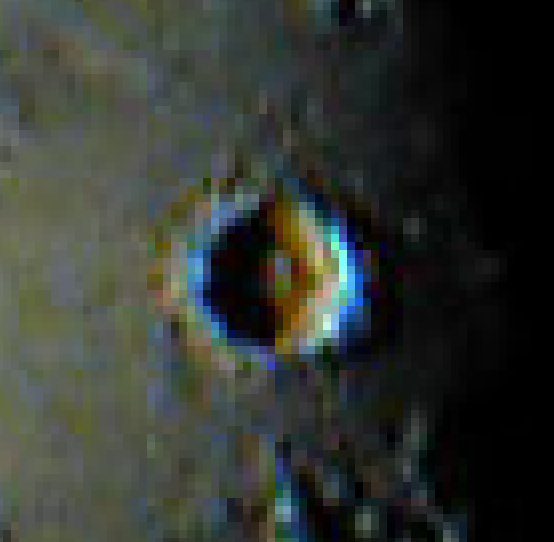
This is called chromatic aberration; it causes bright sources of light to have blue edges on one side and red edges on the other, as in this picture of the Moon:
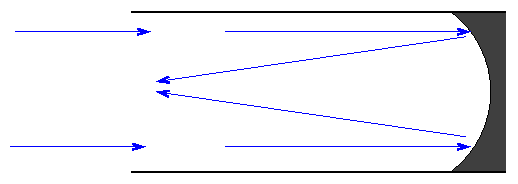
Isaac Newton realized that mirrors would solve the second problem: they can bring light of ALL wavelengths to a common focus. He designed a telescope which used mirrors to reflect light; hence, this type is called a reflector.
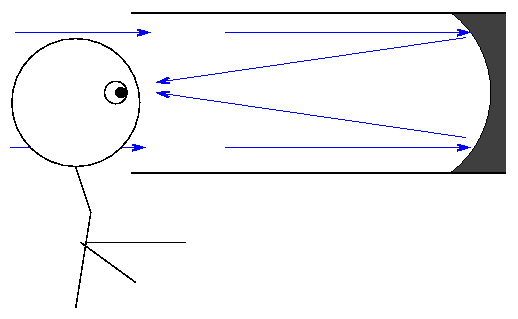
There's a problem with reflectors: they bring light to a focus directly in front of the primary mirror, which isn't such a good idea:
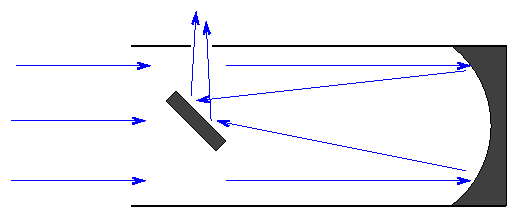
Newton avoided this problem by inserting a secondary mirror near the top end of the tube; the flat secondary simply directs the focusing light rays out the side of the tube, where one can place an eyepiece or instrument without blocking the aperture. The secondary mirror does block a little of the incoming light, but the tradeoff is worth it. We call this a Newtonian reflector.
Another common design, called Cassegrain or (with a front collecting plate) Schmidt-Cassegrain, uses the secondary mirror to send light back down through a hole in the center of the primary mirror.
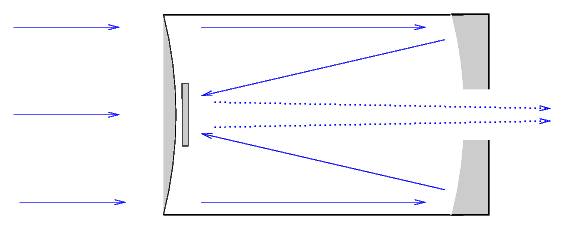
The mirror in a reflector can be supported not only around the edges, but also all over the back surface. That means that very large mirrors can be placed into telescopes. The Subaru Telescope has a primary mirror over 8 meters in diameter.
Why build large telescopes? There are two reasons, one slightly important, and one VERY important.
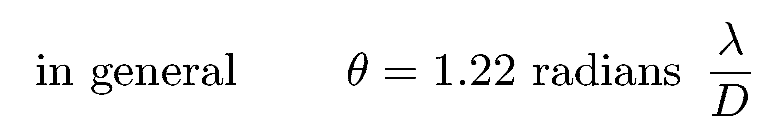
where θ is the angular size in radians, λ is the wavelength, and D is the telescope diameter. If we choose a wavelength in the middle of the visible range, λ = 500 nm , and convert from radians to arcseconds, and express the diameter D in meters, then we find
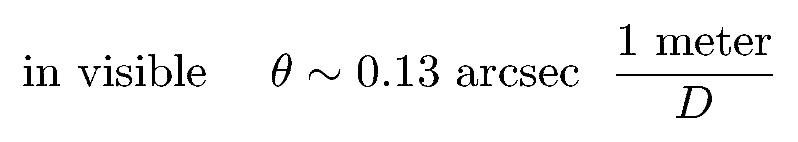
Q: What is the diffraction limit for an 8-inch telescope?
In theory, then, even a modest little telescope should be able to reveal very fine details within lunar craters and Jovian cloud belts.
Thanks to Bill Arnett for the lunar image!
Unfortunately, it doesn't work that way in practice. The Earth's atmosphere is constantly moving, and different layers bend the light from a star in different directions, blurring our view from the ground.
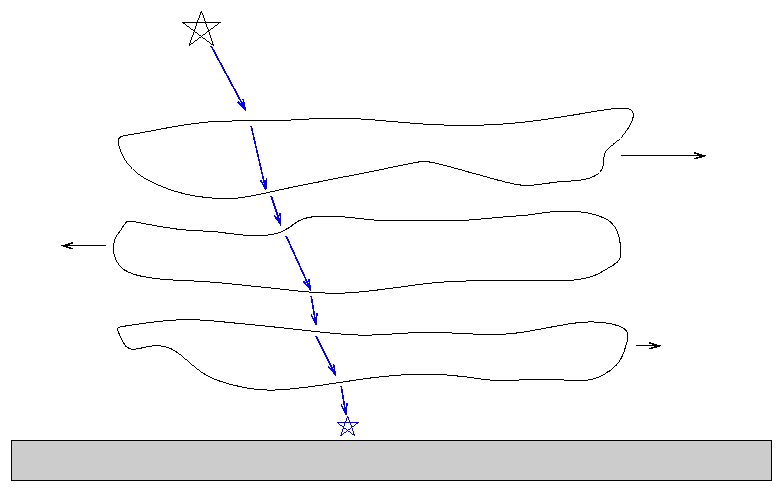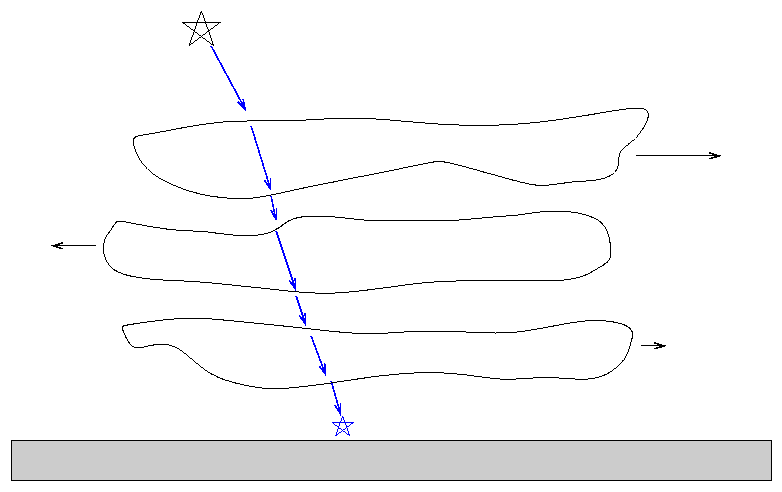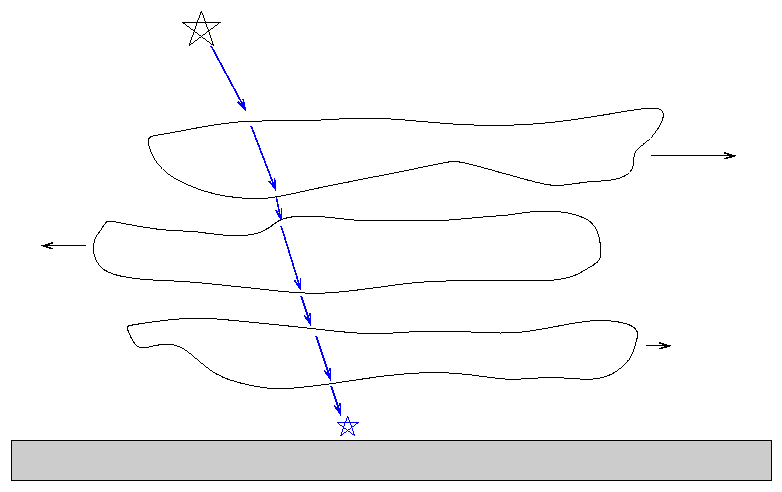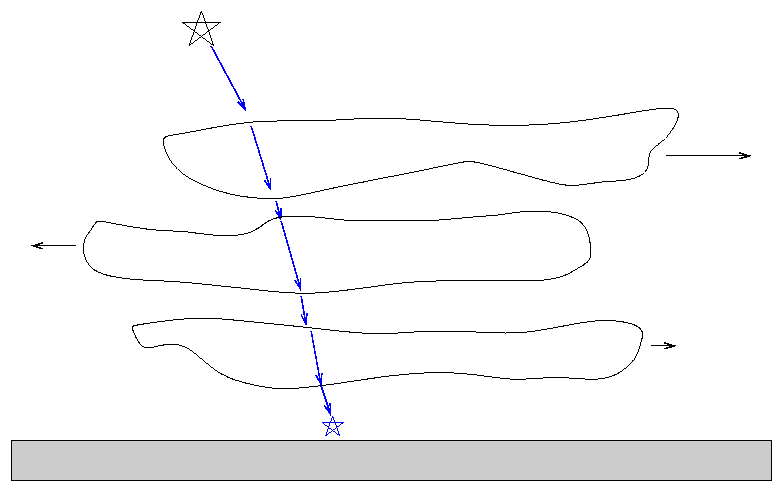
To a rough approximation, the Earth's atmosphere blurs everything to a minimum resolution of about 1 arcsecond (slightly less at good sites, slightly more at poor ones like Rochester). The picture below shows an example of the atmosphere's effect on telescopic images: it shows a view of the star Betelgeuse from the 4.2-meter William Herschel Telescope.
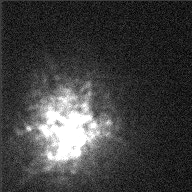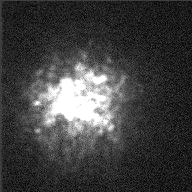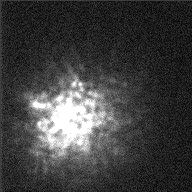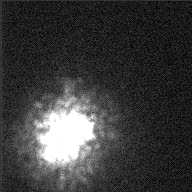
Image courtesy of
the Applied Optics Group of Imperial College and the
William Herschel Telescope
For more details, see
Astronomy Picture of the Day for 2000 July 25
In order to see really fine detail in the optical, you have to move your telescope above the atmosphere:
For example, compare these images of Jupiter taken above the Earth's atmosphere (by the 2.4-meter HST), and below the Earth's atmosphere (by the 2.1-meter Nordic Optical Telescope):
The real reason astronomers want big telescopes is to detect
fainter and fainter objects.
The faintest object visible in a telescope depends on
the amount of light the telescope can gather ...
which in turn depends on its
collecting area:
2
area = pi * (radius)
Note that the collecting area increases as the square
of the radius (or diameter).
Q: The pupil in your eye has a diameter of about 5 mm.
The little telescope at the front of the class has a
diameter of about 4.25 inches = 108 mm.
What is the ratio of collecting area of the telescope
to collecting area of the eye?
How many times fainter are the faintest objects you can see
in the telescope, compared to the faintest object you can
see with your naked eye?
The Pleiades is a pretty cluster of stars you can just barely see with your naked eye (picture on left); with the small 4.25-inch telescope mentioned above, you see MANY more stars (picture on right).
At some point, however, even though you can support your big mirror across its entire back surface, the mirror becomes so big and so heavy that it starts to sag. Even worse, as you move your telescope to point to different regions of the sky, your mirror will sag in different ways. The mirror will no longer bring all the light rays to a single focus. Our current technology has just about reached that point with mirrors of diameter 8 meters.
Q: What can you do if you want to see even fainter objects? A: use an array of smaller mirrors.
The Keck Telescopes feature segmented primary mirrors which total about 10 meters across.
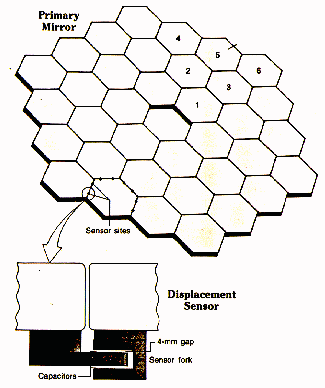
The Hobby-Ebberly Telescope has a slightly larger diameter, though its effective diameter depends slightly on the direction it points.
All the plans to build very large ground-based optical telescopes in the future involve segmented mirrors. Some of these proposed projects are:
which has
just started construction (sort of).
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.