
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
We've looked in great detail at the case of two blocks joined by three springs, so let's move up to THREE identical blocks connected by FOUR identical springs.

We can, if we wish, use exactly the same methods for this 3-block system as we did for the simpler 2-block system. For example, we can choose the matrix route.
First, we write equations for the forces on each block:
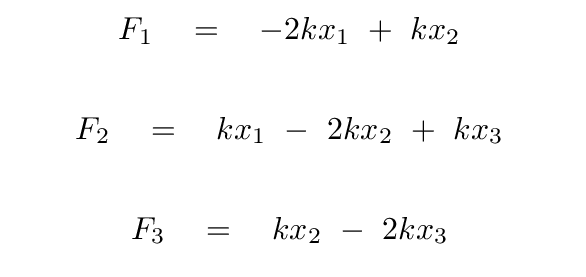
Then, we assume that it will be possible to create some linear combination of the positions of the blocks -- x1, x2, x3 -- which will exhibit simple harmonic motion with some angular frequency ω. These normal coordinates allow us to replace the second-order derivatives with a negative constant times the normal coordinates themselves.
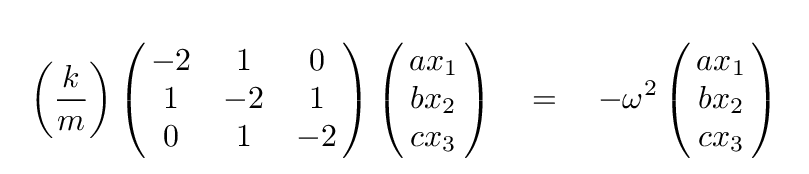
Once we have this standard maxtrix equation, all we have to do is the find the eigenvalues and eigenvectors. After a bit of matrix arithmetic (or perhaps the use of a good mathematics package), we find that the eigenvalues correspond to these frequencies:
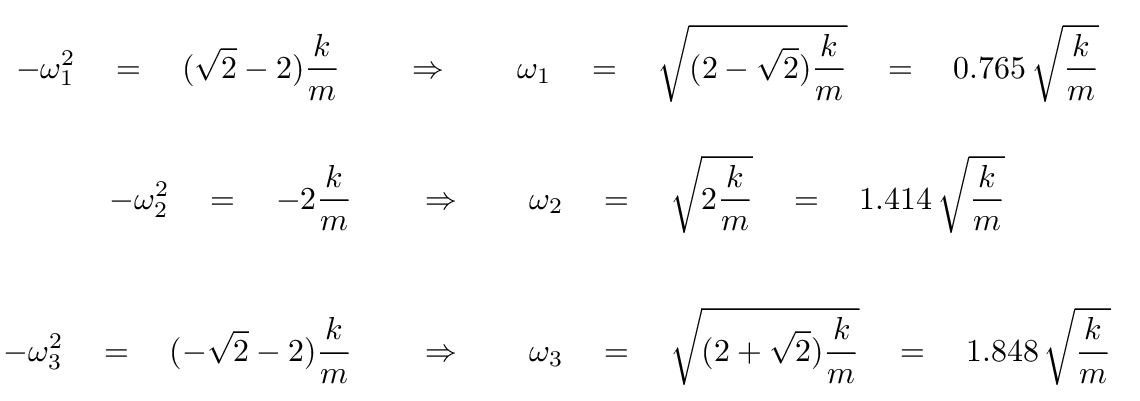
For each eigenvalue, we then derive the corresponding eigenvector. These will give us the proper mixture of the real coordinates to create each of the normal modes. Again, after some algebra, we can find
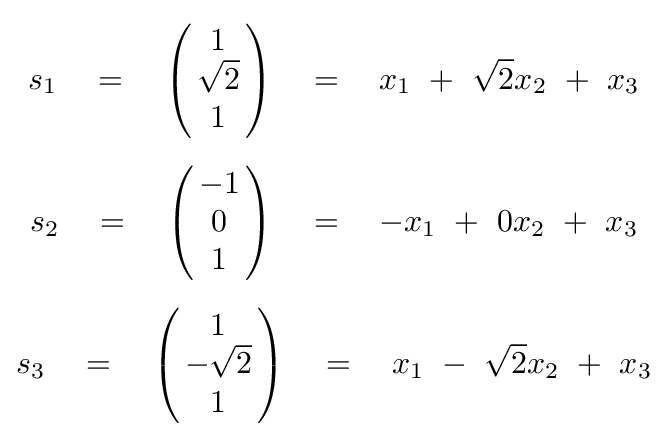
We know that the normal modes involve simple harmonic motion which can be described as
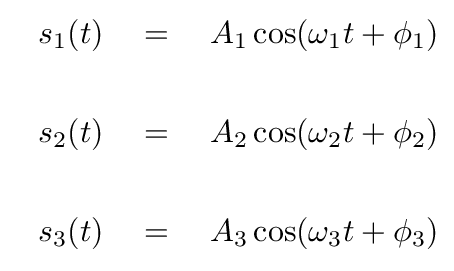
Q: How can we determine the parameters A1, φ1, etc.?
By using the initial conditions, of course.
Finally, we can invert the eigenvalue equations, which express s in terms of x, to find the positions of the blocks in terms of the eigenvectors. In this case, for example, the position of the block x1 is given by
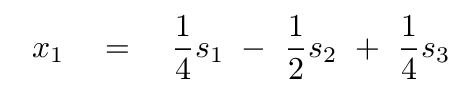
Let's look at the general properties of this system. In the normal mode with the smallest frequency, the outer blocks move in the SAME direction, while the inner block copies their motion, with a slightly larger amplitude (larger by a factor of √2, in fact).
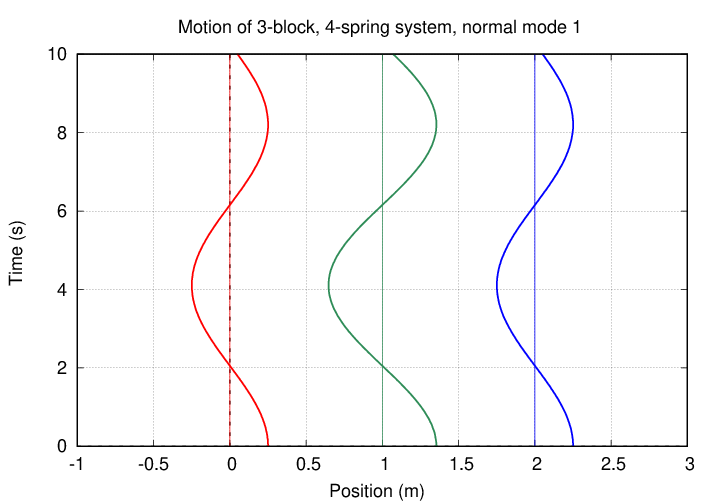
The second normal mode features the outer blocks moving in opposite directions while the central block remains motionless.
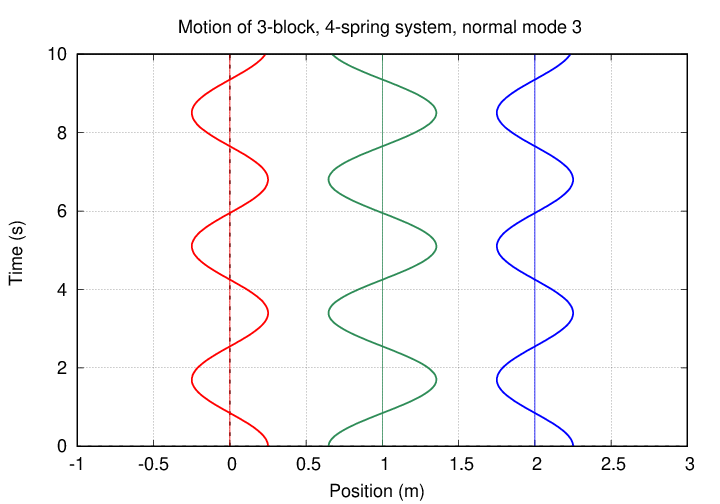
In the third mode, the inner block moves OPPOSITE to the motion of the outer blocks.
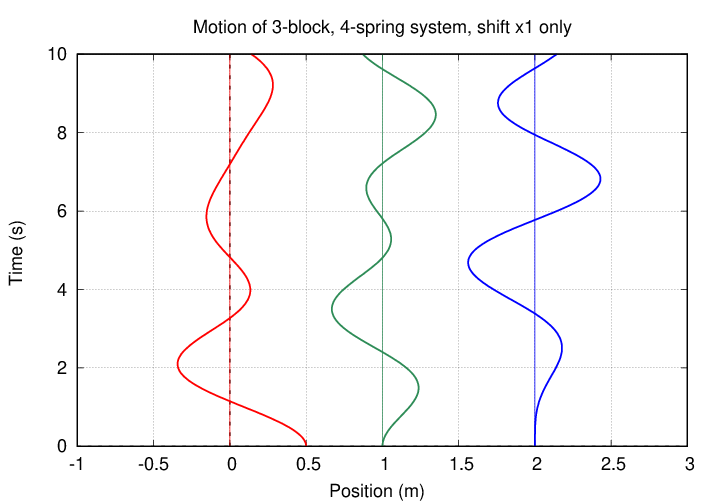
Suppose that we set things up so that the blocks are all motionless at time t = 0. We will leave blocks 2 and 3 at their equilibrium positions, but shift block 1 a small distance to the right. When we release the blocks, quite a complicated pattern emerges.
Before we move on to larger values of N, let's pause to examine the properties of the eigenvalues we've determined for the simple systems.
For two blocks -- N = 2 -- we found
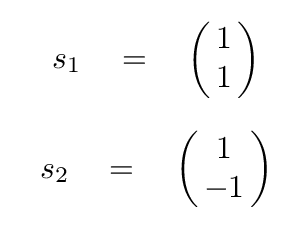
Q: Is it possible to create s2 by some
product or sum of s1?
Nope.
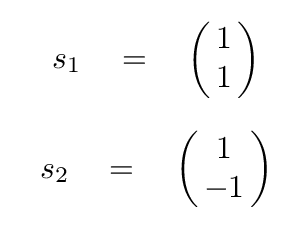
Q: Is it possible to create ANY 1-by-2 vector by
combining some multiples of these two vectors?
Yes, indeed. Just pick two numbers and try it!
Now let's look at the eigenvectors for the three-block system.
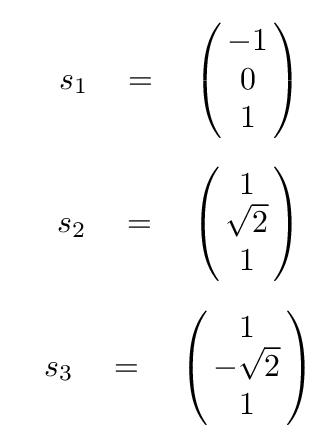
These vectors are similar: each one cannot be made by any combination of its siblings; but, together, the eigenvectors can be mixed to create any other arbitrary 1-by-3 vector.
In other words, the eigenvectors -- which describe the normal modes of these coupled oscillators -- are independent of each other. That makes them a good choice for serving as the basis for describing the myriad possible behaviors of the multiple-block systems.
Let us increase the number of blocks to four, keeping all the masses identical and all the springs identical, too.

Q: Can you guess what the matrix equation for this system is?
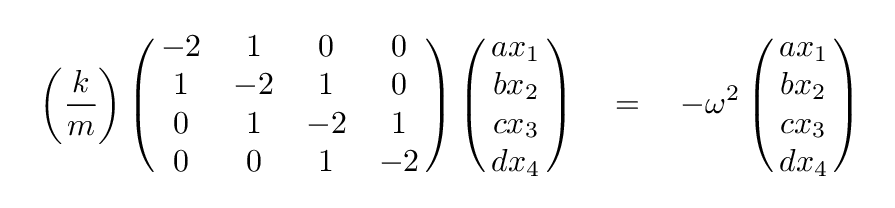
There's a pattern to this matrix: the diagonal elements are all -2, and each is surrounded by a single set of 1 on either side. It's pretty easy to write this out, even for systems with more than four blocks.
Once again, we can use any standard software package (or lots of paper) to find the eigenvalues and eigenvectors of this system. I broke down and used such a package, which gave me
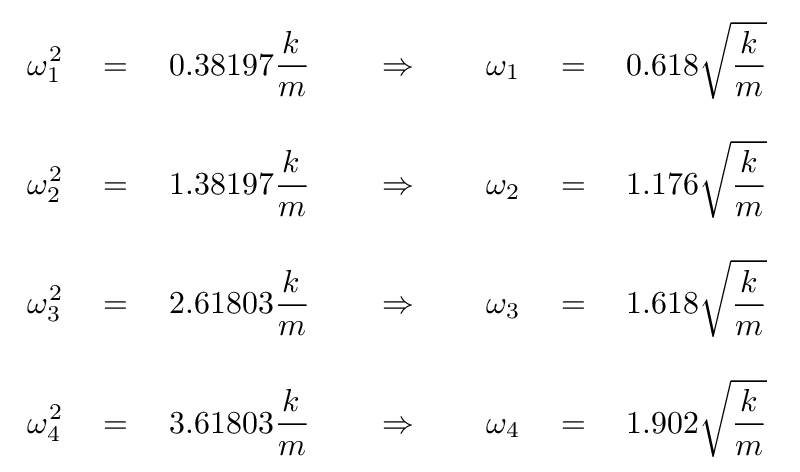
The corresponding eigenvectors are
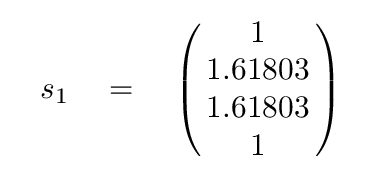
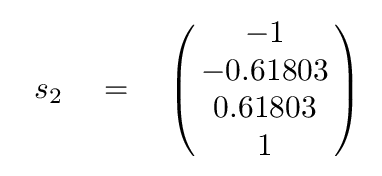
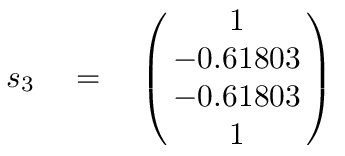
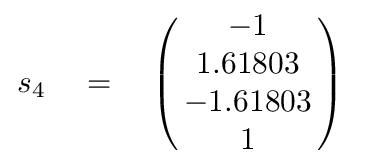
It may not be obvious, but these vectors are also independent of each other.
Let's look at the normal modes of oscillation.
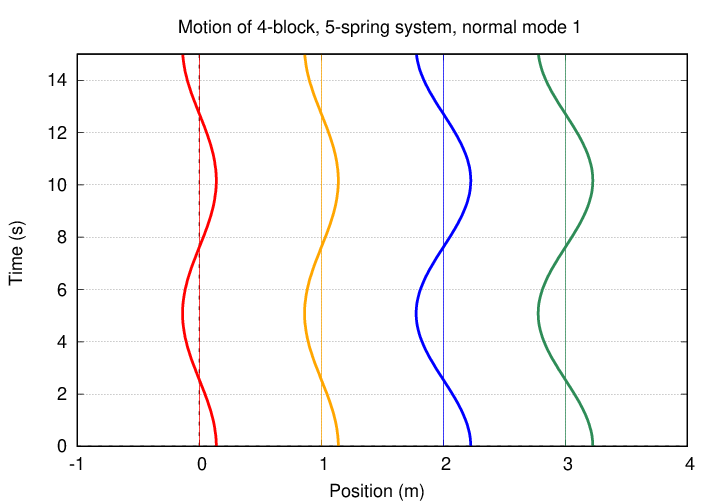
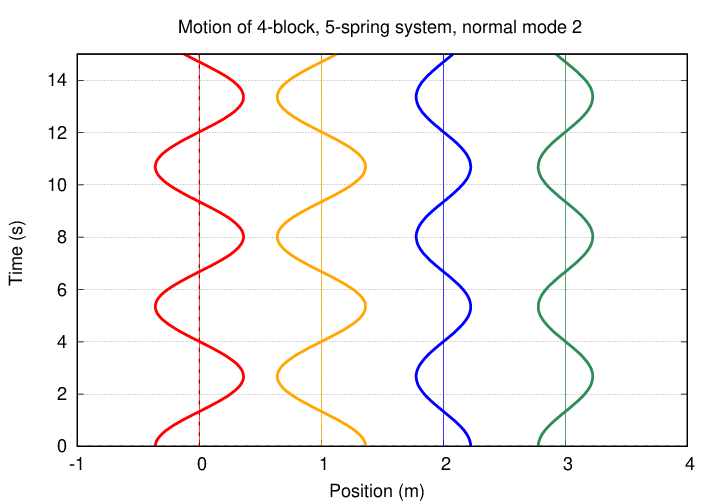
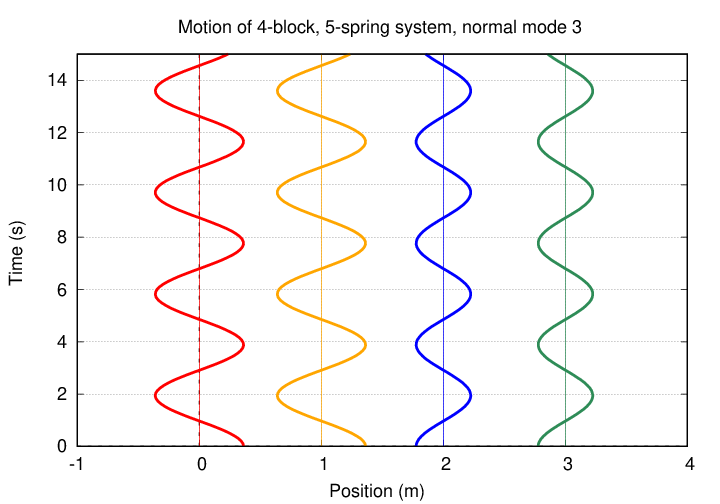

If we begin with all blocks at rest, and at equilibrium, but then shift the first block a small distance to the right, the subsequent motion of the system looks like this:

It is possible to continue this same procedure in order to analyze systems of 5, or 10, or 100, blocks. Just keep making bigger and bigger matrices, following the same nearly diagonal pattern of non-zero elements in the series 1, -2, 1.
But there are some short-cuts which one can make in the simplest version of this problem. If a system of N blocks consists of
then as we shall see in two weeks , it turns out that the angular frequencies of the normal modes are given by this formula:
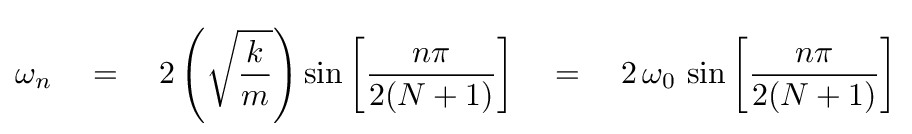
You can check this against some of the frequencies mentioned earlier in this lecture.
(all frequencies multiplied by √(k/m))
N = 2 1.0 1.732
N = 3 0.765 1.414 1.848
N = 4 0.618 1.176 1.618 1.902
If we express these frequencies in terms of the lowest value, we find
(all frequencies multiplied by √(k/m))
ω1 ω2 ω3 ω4
N = 2 1.000 ω1*1.732
N = 3 0.765 ω1*1.848 ω1*2.416
N = 4 0.618 ω1*1.903 ω1*2.618 ω1*3.078
Hmmm. No obvious patterns there ... Well, going back to the general formula for these frequencies,
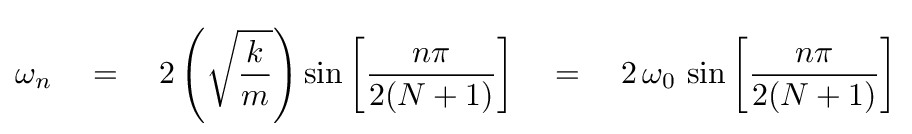
note that if the number of particles N becomes VERY large, then for small values of n (low-order normal modes)
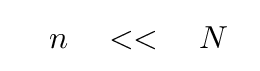
which means
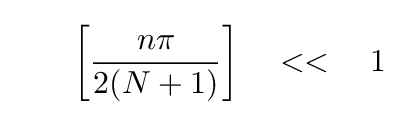
Q: What will happen to the sine function if its argument
is much less than 1?
For small values of x, sin(x) ≈ x. And that means that the normal frequencies of a system with very large number of blocks will be
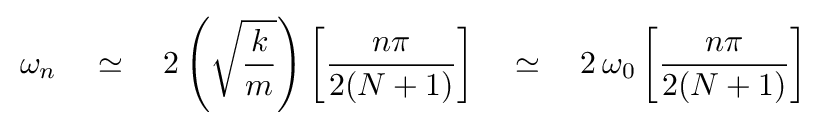
If we re-write this by pulling the factor of n outside the parentheses ...
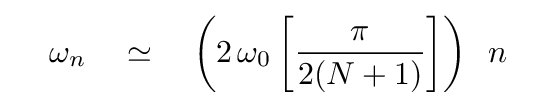
... and recall the expression for the frequency when n = 1 ...
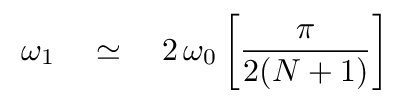
... then it becomes clear that the angular frequencies of the normal modes are simply multiples of the angular frequency of the first mode.
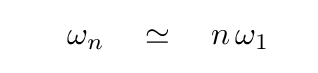
That means that if we look at a system with LOTS of coupled oscillators, we will find
(all frequencies multiplied by √(k/m))
ω1 ω2 ω3 ω4
N = 2 1.000 ω1*1.732
N = 3 0.765 ω1*1.848 ω1*2.416
N = 4 0.618 ω1*1.903 ω1*2.618 ω1*3.078
...
N = 100 0.031 ω1*2 ω1*3 ω1*4
What sort of system contains VERY large numbers of particles, joined together by identical springs? How about a crystal? To a specialist, of course, crystals are much more complex, but for our purposes, they are close enough to apply some of the concepts we've seen. Let's treat a crystal as a set of identical particles, connected by identical springs.
But -- what kind of springs? How strong are the bonds between atoms inside the crystal? In order to compute frequencies of oscillation, we've always needed a force constant k. It's not easy to measure directly the forces between individual atoms, but if we use a bit of indirection, perhaps we can still find those frequencies.
So, let's back up for a moment, and consider a big, macroscopic chunk of salt. Perhaps it can help us to find some way to determine k, or at least some equivalent quantity. We will need to review some of the bulk properties of a solid material -- some ideas you should recall from your first-year physics courses.
For example, consider a long, thin cylindrical object with length L, cross-section area A, and density ρ.
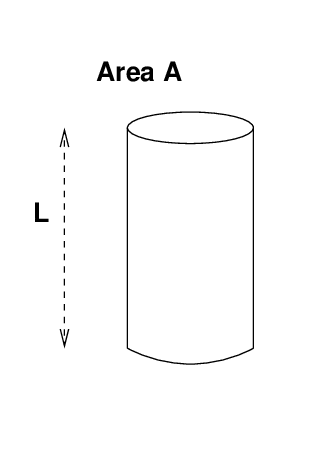
Q: What is the mass of this cylinder?
Now, if we pull on one end of the cylinder, it will deform slightly, stretching by some extra length ΔL. What is the relationship between the force F and the amount by which the cylinder stretches?
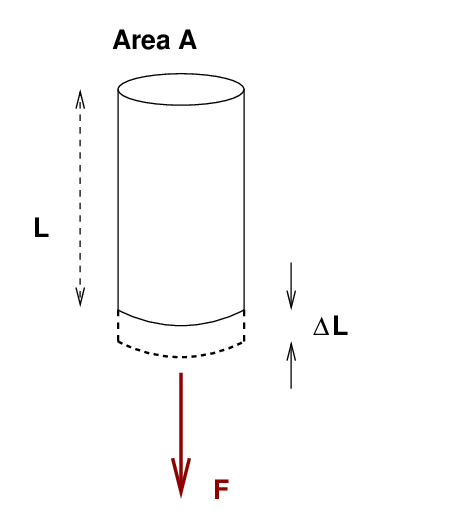
You may recall that Young's modulus for a material defines this relationship:
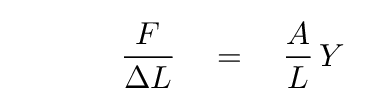
That looks rather similar to the relationship between the force exerted on a spring, and the distance the spring stretches.
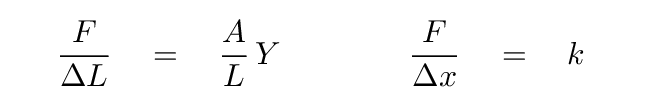
So, if we are interested in the normal modes of many, many oscillators inside a crystal, then we might expect the order of magnitude of the angular frequency of the oscillations to be given, not by
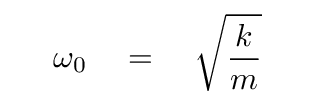
but instead by
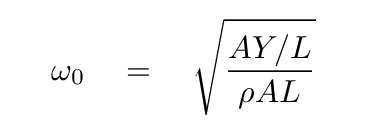
Q: Simplify this equation.
Our expression for angular frequency now contains MOSTLY some quantities of the bulk, macroscopic material, which are easy to measure in a lab. At this point, we are going to cheat just a little, and go back to the microscopic view. For the distance L in this formula, we will insert the distance between adjacent sodium and chlorine atoms, not the length of an entire crystal of salt. This inter-atomic spacing is something that we CAN measure in the lab, too, using, for example, X-ray diffraction techiques (just wait until you take the advanced physics lab course).
Q: Plug in values for sodium chloride:
Y = 40 GPa
L = 0.28 nm
ρ = 2164 kg/m^3
Q: In what part of the electromagnetic spectrum is this angular
frequency?
You should find that this quantity ω0 has a value of about 1.5 x 1013 rad/s. The corresponding frequency, in Hz, is
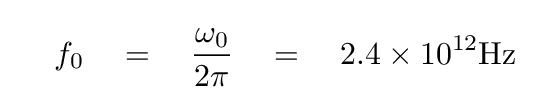
which lies in the terahertz range. The corresponding wavelength is
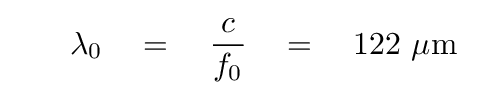
Now, the angular frequency of the n'th normal mode is given by the formula we saw earlier; note the factor of "2" out in front.
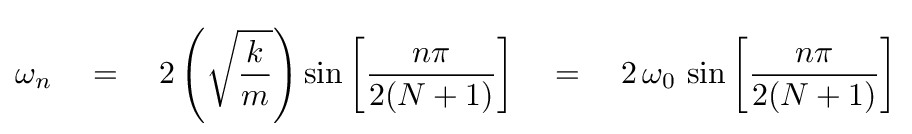
Thus, we expect the highest-energy excited mode, the one with n = N, to have

Q: What is the shortest wavelength at which light should be
absorbed or emitted by a salt crystal?
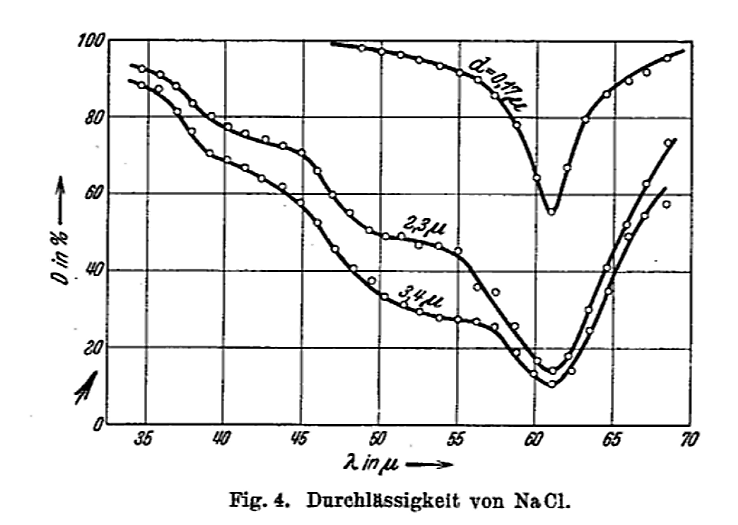
Figure 4 taken from
Barnes, R. B., Z. Physik, 75, 723 (1932)
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.