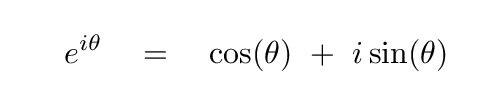
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
The usual Fourier series is a combination of sines and cosines. Since you've seen that one can use a sort of exponential notation to represent sines and cosines, you might guess that it is possible to write a Fourier series using that exponential notation. Indeed it is.
We'll need to use some information you've seen before. First, that e raised to an imaginary angle yields
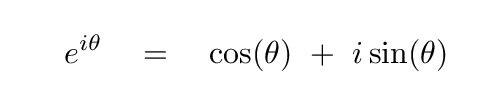
Second, that every complex number
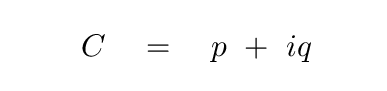
has a complex conjugate
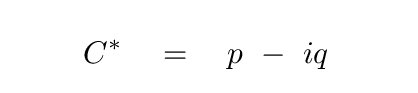
which is defined so that the sum of a complex number with its complex conjugate will yield a purely real result.
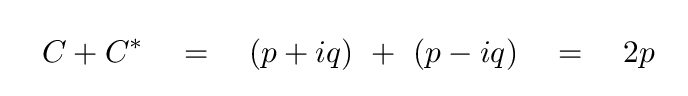
So, let's see if we can use that information to find a way to express the usual Fourier series in a new way. Note that the usual Fourier series
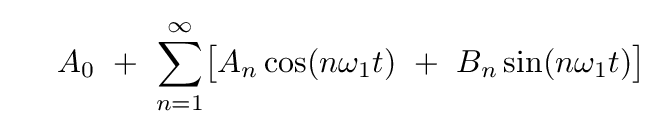
is completely real; there are no imaginary components. So, if we want to produce the same result with exponential notation, we need somehow to get rid of all imaginary pieces. That sounds like a job for the complex conjugate!
Let's guess that we might be able to find some complex coefficients Cn which will make the two series equal:
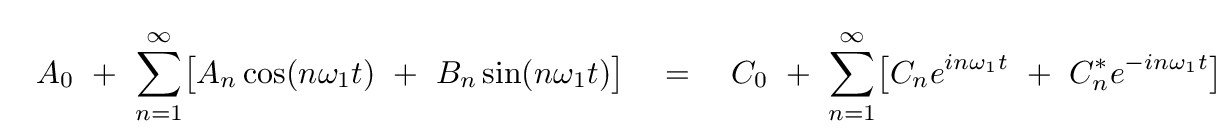
Well, on the left-hand side, we have a series of terms which oscillate at many different frequencies, and on the right-hand side, we have another series of terms which oscillate at many different frequencies. It seems reasonable that the way to make the two sides equal is to ensure that the terms on each side which oscillate with any particular frequency will be equal to each other.
So, for example, the n=0 term, which oscillates at frequency zero -- in other words, the constant term -- must be the same in both cases. That means
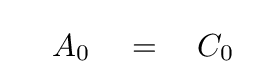
The case for n=1, with frequency ω1, is a bit more complicated:
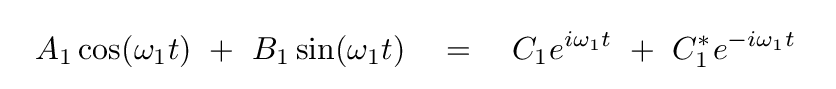
Now, our goal is to find the complex coefficients C and C* which yield the same result as the ordinary sine and cosine terms. We'll need to do a bit of algebra, and it will help to make things concrete if I write down explicit components of these complex values. So, let's say that the real part of C is "p", and the imaginary part of C is "q".
Then we can write this n=1 term of each series as
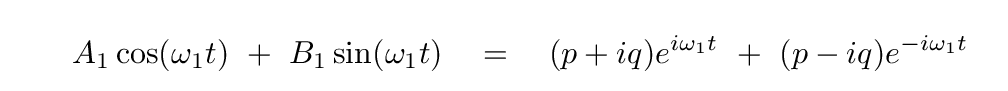
Q: Can you express the right-hand side in terms of sine and cosines?
You should find
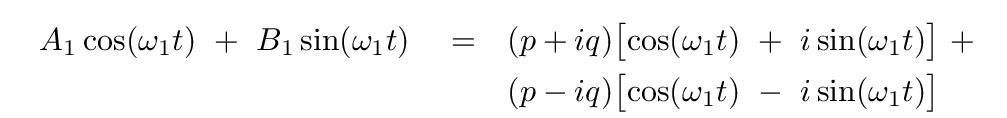
Q: Can you expand the products on the right hand side?
The answer should look like
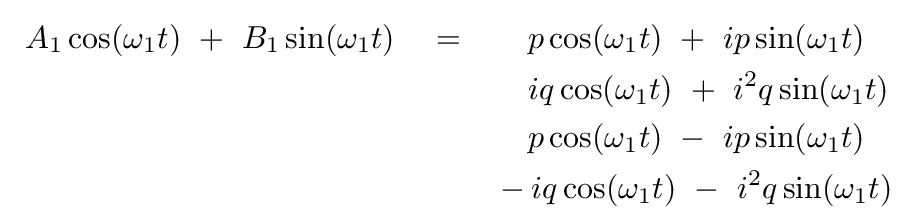
There are eight terms on the right-hand side, but if you look carefully, four of them cancel. If we collect the remaining terms, we end up with
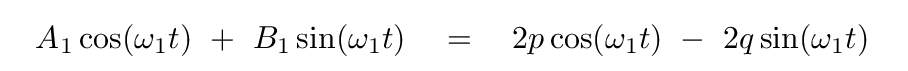
Q: Solve for "p" and "q" in terms of the usual coefficients A1 and B1.
And so our quest is finished. The complex coefficients of the exponential series for n=1 are
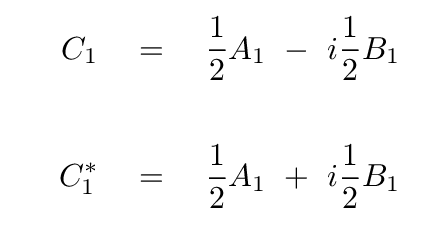
Similar relationships exist for all n greater than 1.
Q: We have seen that a square wave can be written as a Fourier
series starting like this:
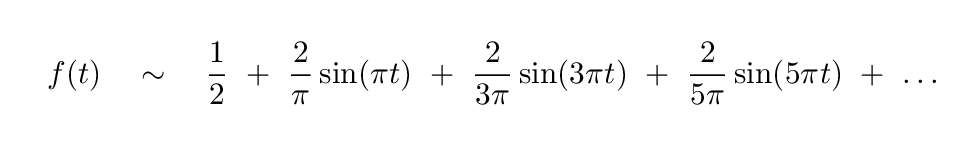
How could one write this as a sum of exponential terms?
Fourier series have a special relationship with functions that are mathematically described as "even" and "odd". Given some function f(t), we can determine if it is even, or odd, or neither, by examining its behavior in the neighborhood of the origin.
For example, Fred measures the motion of a mass hanging from a spring, using his trusty video camera. He records several minutes of it bobbing up and down, and then zooms in on a short section of the video. He picks frame 34 as the start of his time axis.
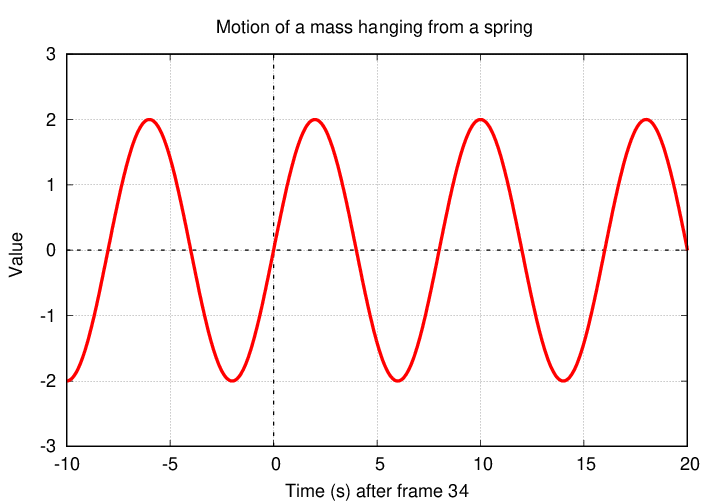
To determine if a periodic function is even or odd, look at its behavior between -P/2 and +P/2, where P is the period.
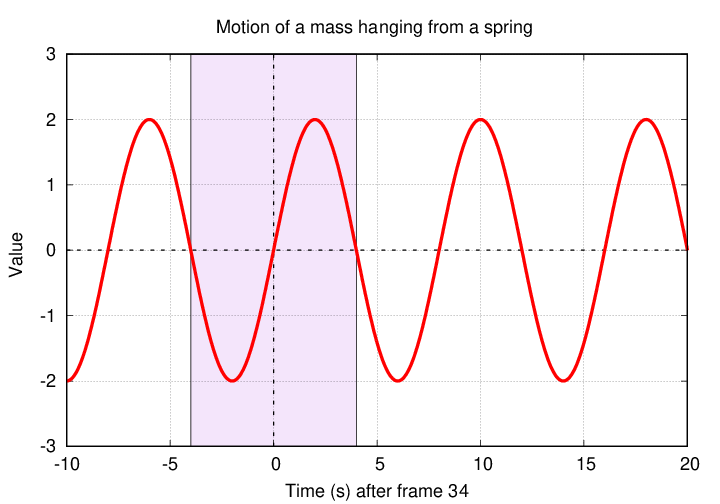
The rule is
Q: In the example above, is the motion of the weight an even function,
an odd function, or neither?
In this case, the motion is an odd function of time.
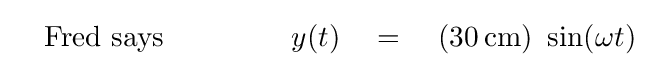
Why is this relevant to Fourier analysis? Because cosine functions are all even, and sine functions are all odd. If one is building a model purely out of sine functions, the result must be odd; a model composed purely of cosines must be even. In other words,
If a function is odd, all the cosine terms = 0 (except maybe A0)
If a function is even, all the sine terms = 0
So, if your job is to find the Fourier components of a function, you can save yourself some time by looking at the form of the function: if it happens to be even or odd, then you can immediately set half of all the components to zero.
Now, there is one twist to this useful fact: if a function is periodic, then its classification into even or odd can depend on one's choice of the origin.
Look again at the video recording of the motion of the weight as a function of time. Fred had a long string of measurements, and he chose to start his clock at frame 34.
But his lab partner, Jane, thought that stretch of video had too much noise. She decided to start keeping track of time with frame 49.
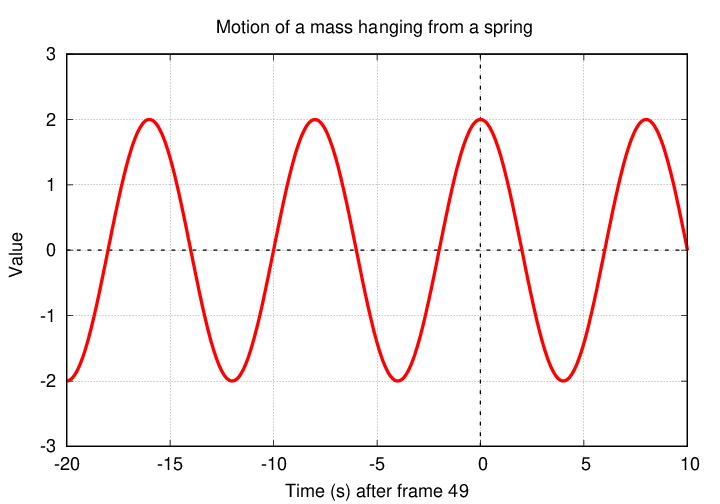
It's exactly the same set of measurements; Jane simply moved the time axis.
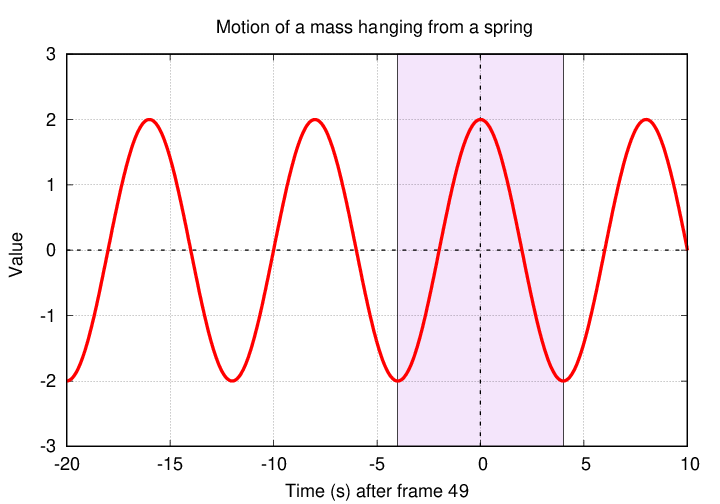
Q: According to Jane, is the motion of the weight even, odd, or neither?
According to Jane, the motion is an EVEN function of time.
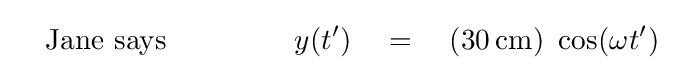
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.