
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Last time, we investigated the quantity known as "Q" in discussions of forced harmonic systems. It has several definitions or meanings. How many can you remember?
What can "Q" mean in a forced harmonic system?
Roughly, low Q means _____________________
high Q means _____________________
More precisely, the numerical value of Q tells us ...
a)
b)
c)
Today, we'll look at another meaning or two of Q.

Ordinary radio stations transmit in two regions of the spectrum:
Each region can contain many stations, especially near big cities. In Rochester, a partial list of the FM band shows (in units of MHz)
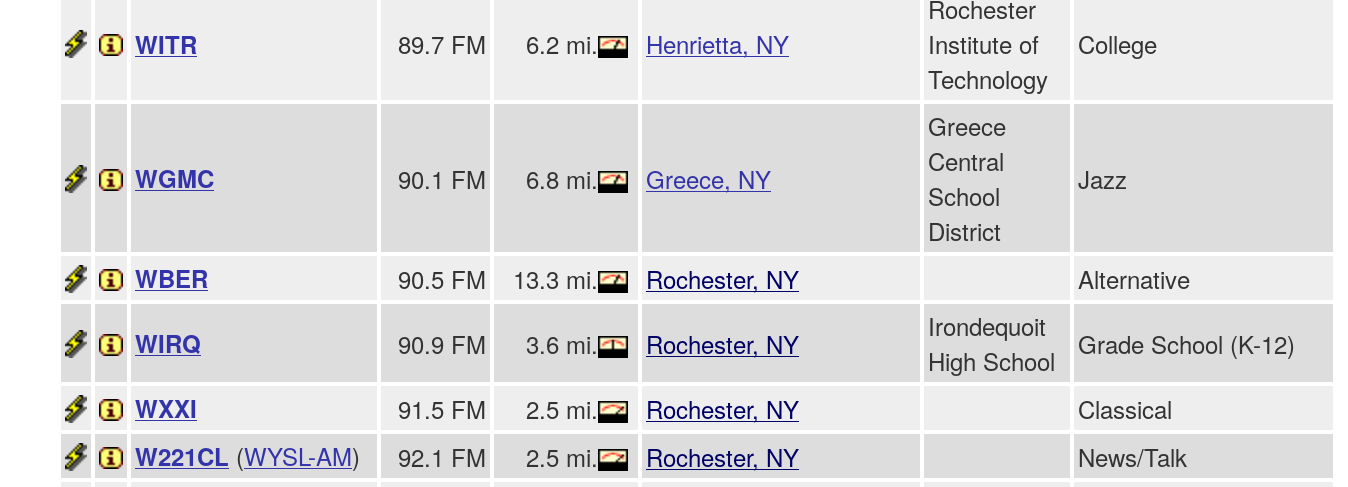
Image courtesy of
radio-locator
Q: What is the typical spacing between stations?
Q: Compute the bandwidth (Δω / ω) which corresponds to this spacing.
Note that the fraction (Δf / f) is the same as (Δω / ω)
Q: What value of Q corresponds to this bandwidth?
(Actual radio tuners need much higher values of Q
to distinguish between weak signals from distant
stations and to reduce noise from crosstalk)
Just for fun, here's a little example with some real sounds. Suppose there are five radio stations:
What will we hear if our radio has a relatively low Q factor?
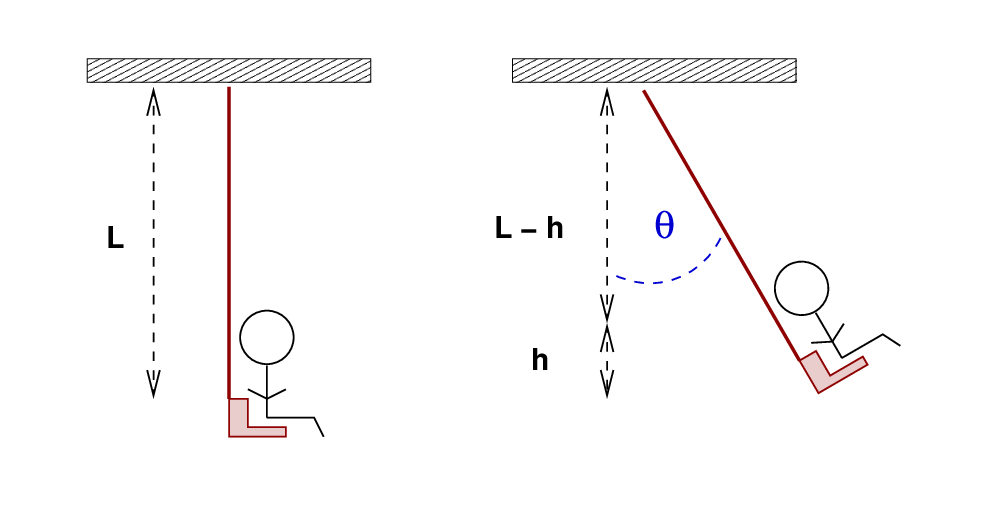
Alice rides the swings at her neighborhood playground.
Q: What is ω0?
After reaching an angle of θ = 15 degrees, a tired Alice stops swinging her legs and just sits motionless. The amplitude of motion decreases to a value of (1/e) times its initial value over the next t = 60 seconds.
Q: What is τ? Q: What is Q?
"Mommy, help!" cries little Alice. Her mother walks over and starts giving her little pushes, at exactly the proper frequency, so that Alice swings higher and higher. However, once Alice reaches the same maximum angle of θ = 15 degrees, her mother modifies her assistance so that the motion keeps that maximum amplitude.
Q: How much power must Alice's mother provide
to keep Alice swinging in this manner?
In many, many, MANY instances, you will be faced with a differential equation to solve, and given some initial conditions which the solution must satisfy. Let's do an example or two in order to see the general method of solving such problems.
Joe is working on a new model of shock absorber for use in elevator safety equipment. His mockup in the lab has a height of 5 m. The plan is for the piston to start at rest at this position, and then slide down towards zero smoothly and quickly. It's okay if the piston goes slightly past zero.
Joe's equipment has properties
In order for the piston to reach equilibrium quickly, Joe modifies the liquid inside the chamber to provide critical damping.
Q: What is the value of b required?
The differential equation to solve is
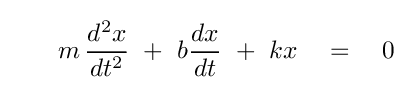
Having taken a vibes and waves class in college, Joe knows that one possible solution to this equation, in the critical damping case, is
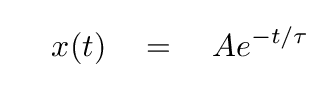
Q: What is the value of the time constant τ?
Joe determines that the initial conditions for his shock absorber are
Q: What value of the constant A will satisfy these
conditions?
The first condition yields
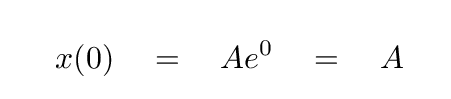
That's easy: Joe sets the constant of integration, A, equal to the initial position: 5 m. Thus, A = 5 m. To check his work, Joe graphs the equation of motion x(t) using this value.
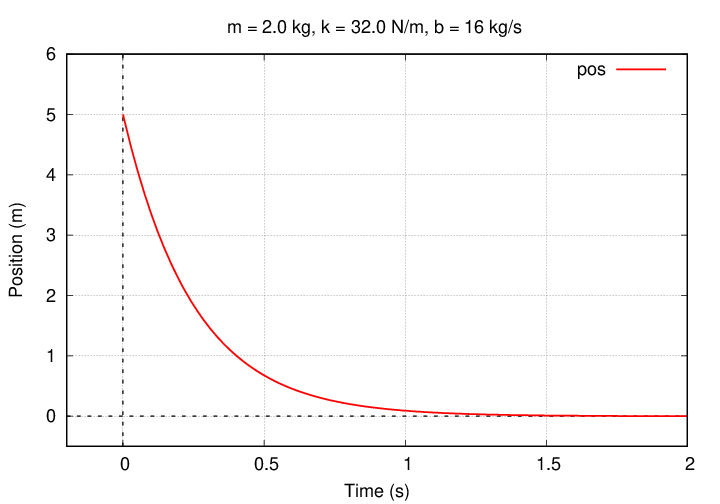
"Looks good!" thinks Joe.
But now Joe checks to see if the second condition, v = 0, is satisfied at time t = 0. The velocity at any time is just the first derivative of position with respect to time, so
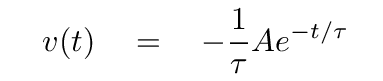
When Joe plugs t = 0 into this equation, he finds
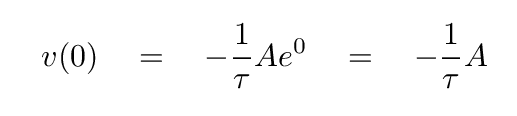
Q: Does this yield a velocity of zero at time = zero?
"Whoops, I'd better double-check that," thinks Joe. Using the value of A = 5 m he determined earlier, he computes the value of velocity as a function of time.
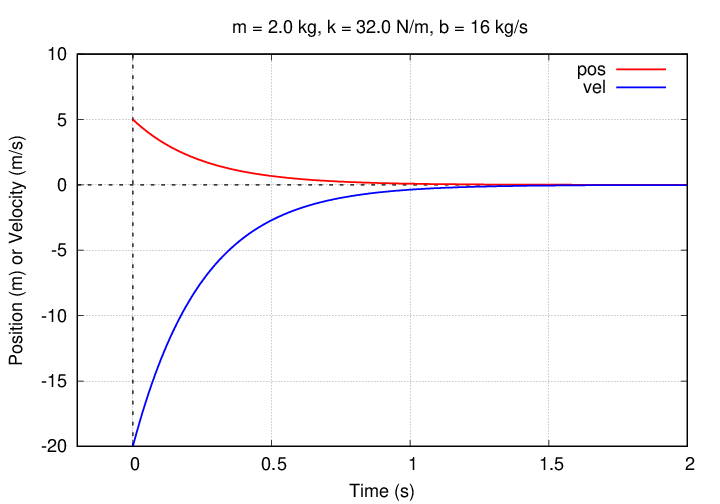
"Rats!" exclaims Joe. "Something is wrong."
Q: What mistake has Joe made? Q: Can you find a real solution?
The key here is that our SECOND-ORDER differential equation
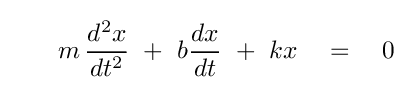
should yield TWO constants of integration. Those TWO constants should be enough to satisfy TWO initial conditions.
What Joe forgot is that there is a second solution to the critically damped oscillator. He should have written
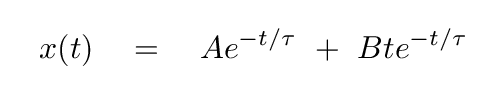
In this case, the velocity is
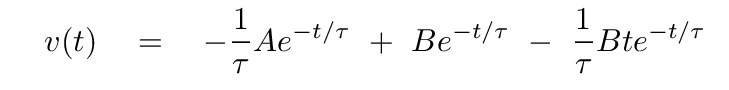
Recall those initial conditions:
This -- and almost all similar problems -- come down to solving two equations (initial conditions) for two unknowns (the constants of integration).
Q: What is the value of the coefficient A? Q: What is the value of the coefficient B?
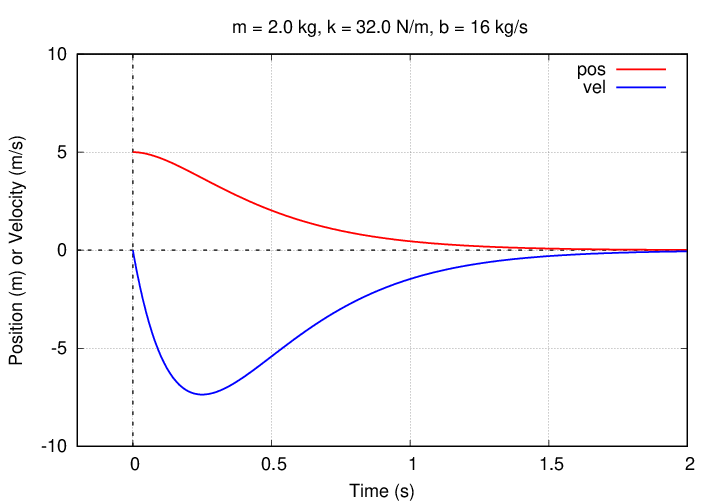
As a check, here is a graph showing the values of position and velocity for this solution.
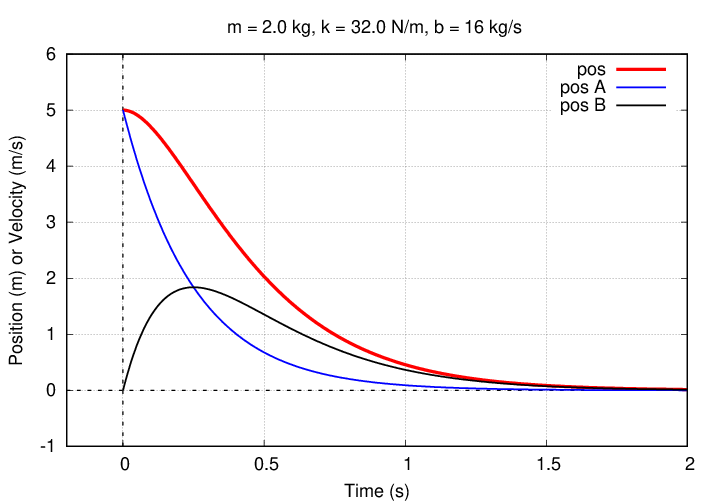
How much of the position, and velocity, is due to each of the two terms in the solution? The graphs below show the contributions from the first term (with A) and the second term (with B). First, position. Note how the A term dominates at early times, but the B term at later times.
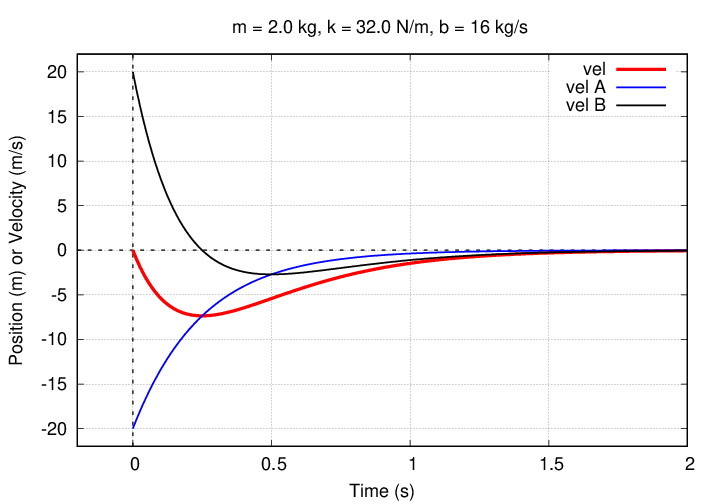
Next, the contributions to the velocity. Once again, the A term is most important at the beginning, but the B term takes over later.
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.