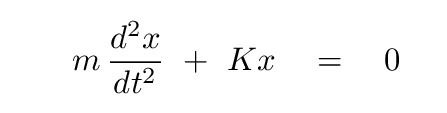
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Today, we'll start with the standard differential equation which leads to SHM, and see what happens if we interact with the equation in a slightly different manner: instead of finding a solution to the equation, we will integrate both sides of that equation. Maybe some useful relationships will appear.
Let's go back to the good old second-order differential equation:
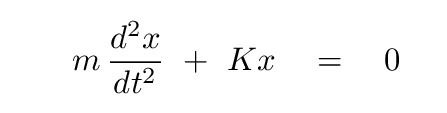
What will happen if we integrate both sides with respect to position, x?
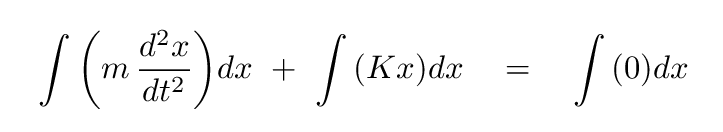
Q: What is the value of the middle term? Q: What is the value of the right-hand side of the equation? Q: What are the units of each side of the equation?
Right. The middle term is easy-peasy to integrate, and it tells us that both sides of the equation must have units of Newtons*meters = Joules -- which means energy.
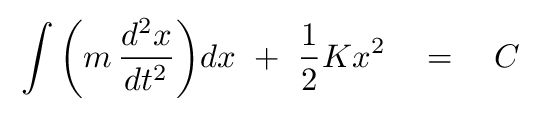
But what about that first term? If we were integrating with respect to TIME, we'd have no problem. But integrating with respect to POSITION means that the solution isn't obvious.
Here's a method which may come in handy in situations with no clear way forward. Try guessing a solution, and then work backwards by differentiating to see if it yields the correct result.
So, let's guess that the integral of the first term looks something like this:
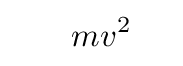
If we take the derivative of this guess with respect to position, we get ... what?
Q: What is the derivative with respect to x of this guess?
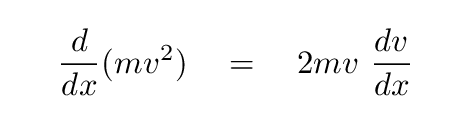
Now, the next step is just a simple re-writing of velocity.
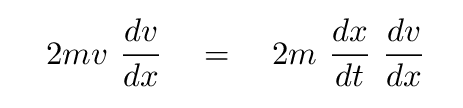
But the critical step comes at this point. If we can treat differentials just like ordinary algebraic quantities, we can cancel the dx terms, right?
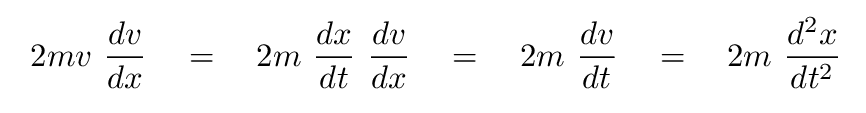
And that leaves us with the second derivative of position with respect to time -- just as required! Yes, there's an extra factor of 2 in our result, but we can fix that easily.
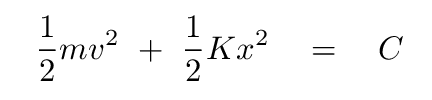
So, in the course of SHM, the velocity changes from zero to a maximum, so the kinetic energy varies constantly; and the position changes from zero to its maximum, so the potential energy also varies. However, if we add the kinetic energy and potential energy together, we will always end up with the same total energy.
Or, in other words, energy is conserved in SHM.
But position isn't the only basis we can choose for integration. Suppose we integrate our differential equation
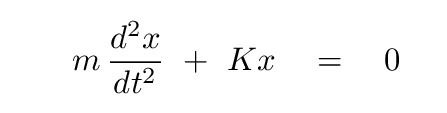
with respect to time, t?
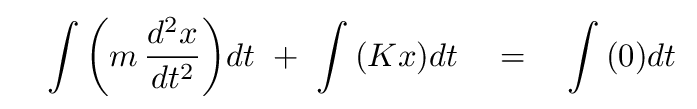
Disclaimer: all the following should include vector signs and dot products and so forth. I'm leaving them out, since this is simply a side note to the main lesson for the day.
We can make one useful substitution at the start. We already know that the magnitude of the force on an object in SHM is K * x, so the middle term could be written as
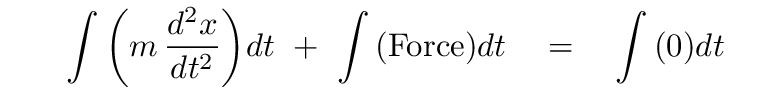
Q: What is the value of the first term? Q: What are the units of each side of the equation?
Right. The first term is easy to integrate, and it tells us that both sides of the equation must have units of kilograms * meters per second -- which means momentum.
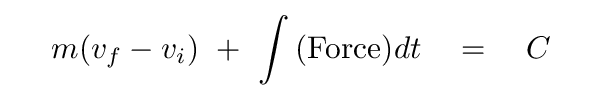
Q: What is the middle term?
You may recall that the integral of force over time is called impulse, and it has units of momentum.
So, if we attach a weight to a spring and set it oscillating in motion, the momentum of the weight itself is definitely not conserved -- after all, sometimes it moves fast, sometimes it moves slowly, and twice each cycle it comes to a momentary halt. But the sum of the weight's momentum and the spring's impulse is conserved.
In general, if one is able to write a differential equation relating the motion of an object to its location in a potential, one may be able to integrate that differential equation to find conserved quantities, which are sometimes called integrals of motion.
We have seen that in SHM, total energy is conserved. There are many other situations in which energy is conserved; for example, the motion of a ball thrown across the room (if we ignore air resistance), or the motion of a planet orbiting around the Sun.
Linear and angular momentum are other quantities that are often conserved in ordinary situations. As you encounter more complicated physical situations, governed by more complicated potential energy functions, you may find other, less familiar quantites which are conserved as well.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.