 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Let's review the observational evidence:
Is there any way to tie all these pieces of data together? Yes! One model which can explain them all is called the Big Bang model. The name was coined by a scientist who didn't like the theory and tried to make it sound silly.
The Big Bang is built upon three main tenets:
Note that the basic Big Bang Model does NOT say anything about the following questions:
Some of these questions all depend upon the values of certain parameters in the model, which we may derive from observations. Others have nothing to do with the Big Bang itself.
Our understanding of the laws of nature permit us to track the physical state of the universe back to a certain point, when the density and temperature were REALLY high. Beyond that point, we don't know exactly how matter and radiation behave. Let's call that moment the starting point. It doesn't mean that the universe "began" at that time, it just means that we don't know what happened before that point.
One of the primary successes of the Big Bang theory is its explanation for the chemical composition of the universe. Recall that the universe is mostly hydrogen and helium, with very small amounts of heavier elements. How does this relate to the Big Bang?
Well, a long time ago, the universe was hot and dense. When the temperature is high enough (a few thousand degrees), atoms lose all their electrons; we call this state of matter, a mix of nuclei and electrons, a fully-ionized plasma. If the temperature is even higher (millions of degrees), then the nuclei break up into fundamental particles, and one is left with a "soup" of fundamental particles:
Now, if the "soup" is very dense, then these particles will collide with each other frequently. Occasionally, groups of protons and neutrons will stick together to form nuclei of light elements ... but under extremely high pressure and temperature, the nuclei are broken up by subsequent collisions. The Big Bang theory postulates that the entire universe was so hot at one time that it was filled with this proton-neutron-electron "soup."
But the Big Bang theory then states that, as the universe expanded, both the density and temperature dropped. As the temperature and density fell, collisions between particles became less violent, and less frequent. There was a brief "window of opportunity" when protons and neutrons could collide hard enough to stick together and form light nuclei, yet not suffer so many subsequent collisions that the nuclei would be destroyed. This "window" appeared about three minutes after the starting point, and lasted for a bit less than a minute.
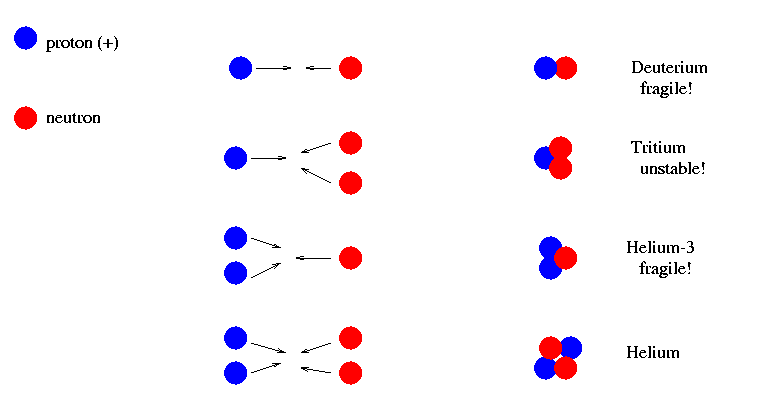
Which nuclei would form under these conditions? Experiments with particle colliders have shown us that most of the possible nuclei are unstable, meaning they break up all by themselves, or fragile, meaning they are easily broken by collisions.

Helium (the ordinary sort, with 2 protons and 2 neutrons) is by far the most stable and robust compound nucleus. Deuterium (one proton and one neutron) is easily destroyed, and so is helium-3 (2 protons, one neutron).
So, it seems that this period of hot, dense plasma would create a lot of helium. Could it create other, heavier elements, too?

It turns out that none of the heavier nuclei which are easily made by collisions of single particles with helium nuclei, or helium nuclei with each other, are stable or robust. Almost all nuclei heavier than helium are likely to be destroyed by subsequent collisions. The only heavier nucleus which might possibly survive is lithium-7 (3 protons and 4 neutrons), but it requires the collision of a helium nucleus plus 2 or 3 other particles simultaneously, which isn't very likely.
Detailed models of Big Bang nucleosynthesis predict that the brief "window of opportunity" lasted only a minute or two. After that, about three and a half minutes after the starting point, the temperature and density dropped so much that collisions between particles were rare, and of such low energy that the electric forces of repulsion between positively-charged nuclei prevented fusion. The result is
The relative amounts of hydrogen, helium, deuterium and lithium depend very sensitively on the exact density of matter in the universe during this window of opportunity. We'll discuss this later.
So, during the first few minutes after the starting point, the universe was hot enough to fuse particles into helium nuclei. The result was a ratio of about 12 hydrogen nuclei to 1 helium nucleus; that's equivalent to saying that three quarters of the mass of the universe was hydrogen nuclei, and one quarter of the mass was helium nuclei.
But these nuclei were totally ionized: they lacked the normal collection of electrons surrounding them. The electrons were free to fly around space on their own. Free electrons are very efficient at scattering photons. Any light rays or radio waves or X-rays in this ionized plasma were scattered before they could travel far. The universe was opaque.
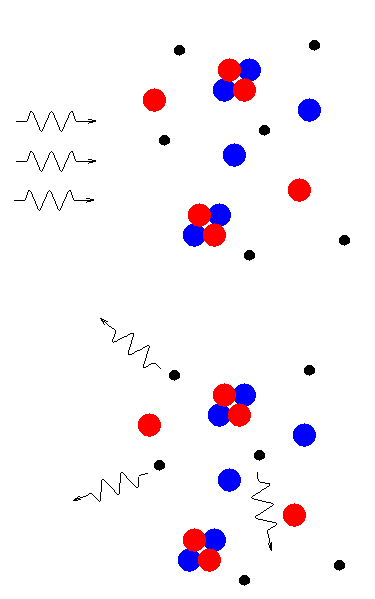
After a few thousand years, as the universe continued to expand and cool, the temperature reached a critical point. About 100,000 years after the starting point, the temperature dropped to about 3,000 degrees Kelvin. At this point, hydrogen nuclei (protons) were able to capture electrons, and hold them against collisions. We call this process of capturing electrons recombination (even though it was really the first "combination", not a re-"combination").
The universe became largely neutral, with electrons bound into hydrogen and helium atoms. Neutral atoms are nearly transparent to light rays and radio waves. Suddenly, the universe became transparent.
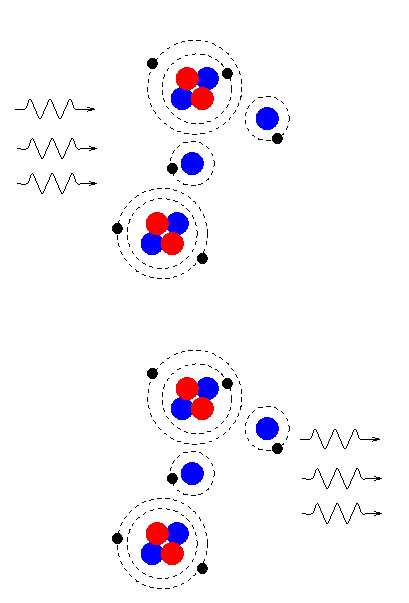
What this meant was that light rays which were produced by the hot, 3,000-degree gas were free to fly throughout the universe without being scattered or absorbed. What kind of photons were they? Since they were produced by a hot gas, they had a blackbody spectrum appropriate for a temperature of about 3,000 Kelvin:
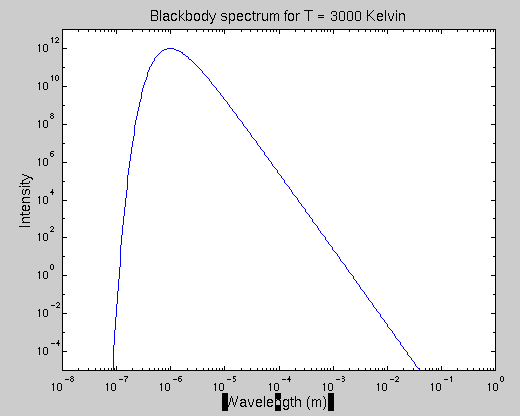
As the universe continued to expand, the wavelength of these photons increased: each time the universe doubled in size, the wavelength of the photons doubled. However, since the wavelength of each photon increased by the same factor, the relative wavelengths of the photons remained fixed. It turns out that when one increases all the wavelengths of a blackbody spectrum by the same amount, one gets another blackbody spectrum -- but one which corresponds to a lower temperature than the original.
The universe has expanded by a factor of about 1,000 since the time of recombination, which means that the wavelengths of these blackbody photons have increased by a factor of about 1,000 as they have flown through the cosmos. The Big Bang theory predicts that we should be able to detect these stretched-out photons, if we look in the right part of the electromagnetic spectrum:
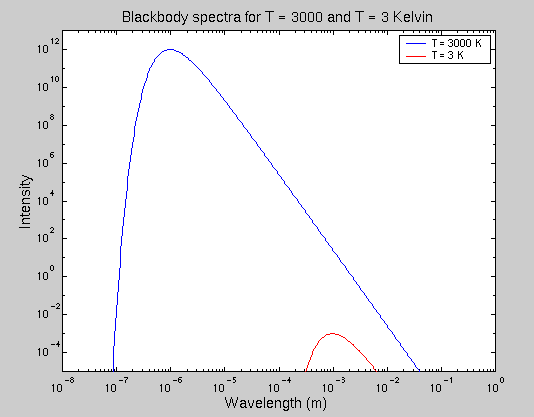
The peak of the shifted blackbody spectrum now falls in the microwave range, with a wavelength of about one millimeter. This corresponds to a blackbody temperature of about 3 Kelvin: a factor of 1,000 times lower than the original 3,000 Kelvin when the gas became neutral. It is reasonable to say that as the universe expands, its "temperature" drops in sync: expansion by a factor of 2 means the temperature drops by a factor of 2, expansion by a factor of 10 means the temperature drops by a factor of 10, and so on.
And when we look at the universe with radio telescopes in the microwave range, we see a spectrum which is exactly like a blackbody ...
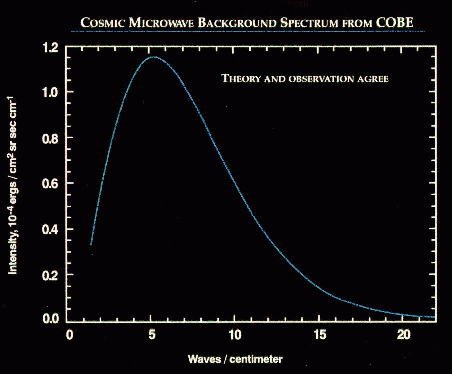
with a peak at a wavelength of 1.869 millimeters, corresponding to a temperature 2.726 Kelvin.
The Big Bang model predicts that this temperature drops as the universe expands. If we could somehow measure the temperature of the CMB at some time long ago, we ought to find a temperature higher than 2.7 Kelvin. And ... we can!
The measurements are very difficult: they involve taking high-resolution spectra of very distant quasars, and looking at absorption by intervening material in galaxies that just happen to lie between us and the quasar. One recent attempt used the ratio of several lines of neutral carbon:
Astronomers have tried to use such measurements to calculate the temperature of the CMB as a function of redshift (and, in turn, as a function of time). Most of the attempts have yielded only upper limits to the CMB temperature in the past, but in December, 2000, a team of astronomers using one of the 8.2-meter Very Large Telescopes in Chile succeeded in making an honest-to-goodness determination: on the plot below, their value is the solid line denoting a temperature 6K < T < 14K at a redshift z=2.34.
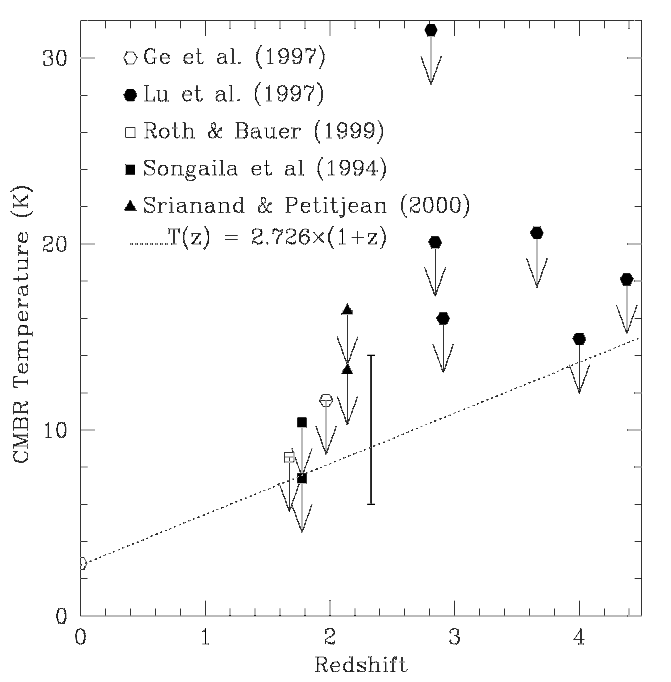
Now, if the universe was perfectly uniform at the time of recombination -- same density everywhere, same temperature everywhere -- then we should see a perfectly uniform microwave background. But, if the gas in the early universe had gathered into clumps by the time of recombination, even very fluffy clumps, the radiation it produced would be slightly more intense in the clumpy areas, and less intense in between them. The amplitude and size of fluctuations in the microwave background can tell us a lot about the conditions of the hot gas just 100,000 years after the starting point. We'll discuss this later...
The Big Bang theory states that the universe is expanding, though it does not explain why the universe should behave in this way. As a result, objects which are subject to no forces should move away from each other. In a uniformly-expanding universe, the rate at which objects move away from each other depends linearly on their distance from each other.
And that linear relationship between distance and radial velocity is just what we see when we look at distant galaxies:
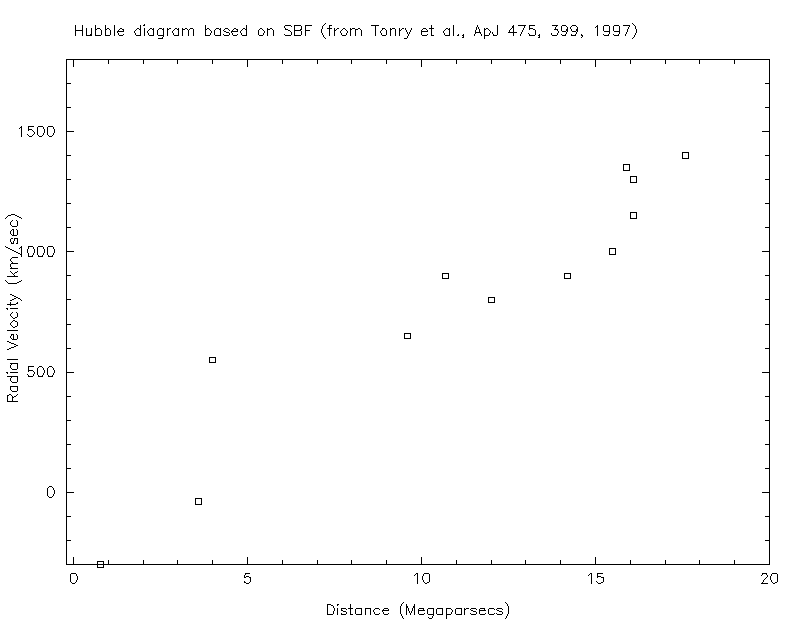
But ... wait a minute. Does this expansion occur on all scales? What about
If there are "significant" attractive forces between objects, they do not move away from each other as time goes by. These attractive forces may be
"chemical" forces between important on microscopic,
neighboring molecules or atoms human, and planet-sized
(these are really due to scales
electric forces)
gravitational forces between important on solar-system,
large bodies of matter galaxy, and galaxy-cluster
scales
So the distance between the Earth and Sun has not increased over the past 4 billion years. Nor does the length of a meterstick grow due to the expansion of the universe.
Only on the very largest scales, distances between isolated galaxies or clusters of galaxies, are the attractive forces so weak that the expansion of the universe is able to move objects apart.
The rate of expansion depends sensitively on the exact amount of matter in the universe. If the density of matter is high, long-range gravitational forces can slow down the expansion, or even stop it. If the density of matter is very low, the expansion will go on forever. We will discuss this in greater detail later.
The Big Bang theory explains
It doesn't provide answers to all our questions, but it does a better job than any alternative which has yet been proposed. All but a handful of astronomers have adopted the Big Bang as the standard theory for the evolution of the universe.
For more information,
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.