
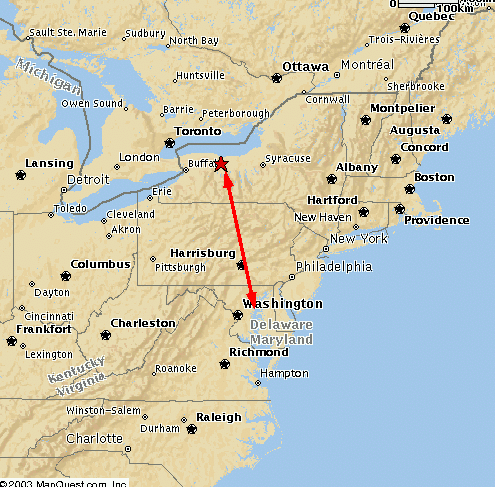
Take a look at an example of city-to-city parallax
Another example of city-to-city parallax
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Astronomers, like most other scientists, describe the world in the language of mathematics. You won't see a great deal of math in this course ...
if you DO like math, consider switching to SPSP 301, University Astronomy, which meets MTWF 5:00 PM in 08-A300.
... but one bit of Euclid's lingo which you must be able to understand is a simple bit of geometry. Namely, the technique by which one can figure out the length of one side of a right triangle. Astronomers use this technique to determine distances to celestial objects -- by measuring their parallax.
In order to use this technique to calculate a distance, you need to know (at least) two things:
So, the basic idea is to look very carefully at the same object from two different places -- that gives you the baseline. If you can detect a shift in the object's position relative to the background, you have the angle. And then you can find the distance.
You will have a chance to use the "parallax" technique to measure a distance in class today. Not the distance to Alpha Centauri, or Saturn, or the Moon; no, you will attempt to measure the distance to your thumb.
Now, there are limits to this technique. As you look at more and more distant objects, the angle shrinks. If the angle becomes too small, you can't measure it accurately. The only thing to do at that point is find a longer baseline.
What are some possible baselines?


Take a look at an example of city-to-city parallax
Another example of city-to-city parallax
But none of these baselines allows us to measure the distance to any star other than the Sun: the angles they provide are just too small. Even the entire diameter of the Earth won't do the trick. Is there any longer baseline we can find?
Yes. We can use the diameter of the Earth's orbit.
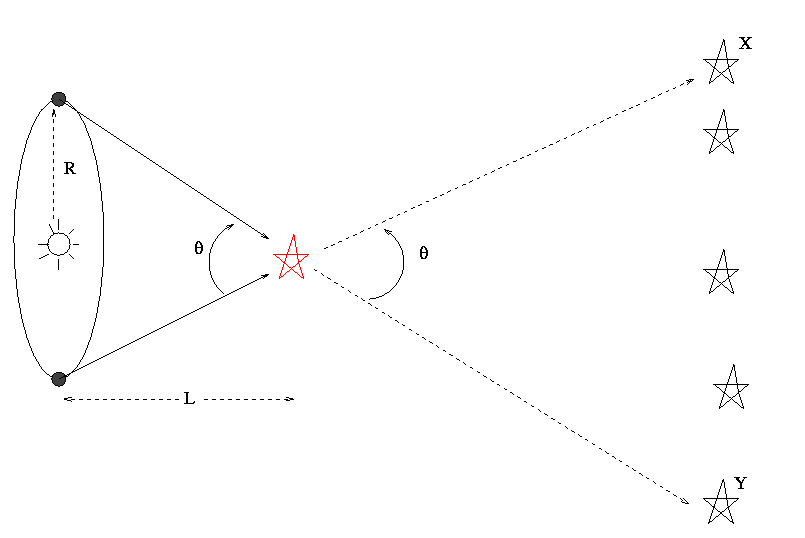
How large is the baseline now?
Time is pretty important to astronomers. Why? Two reasons:
Astronomers have always been good time-keepers. In fact, during the fifteenth through nineteenth centuries, they were given the very important job of keeping the official time in most European (and American) countries. Back then, ships needed to re-set their clocks every time they came into port. Navigators needed to know the time to figure out their longitude. Without an accurate time, captains didn't know exactly where they were ... which could lead to disaster.
But how many different kinds of time are there?
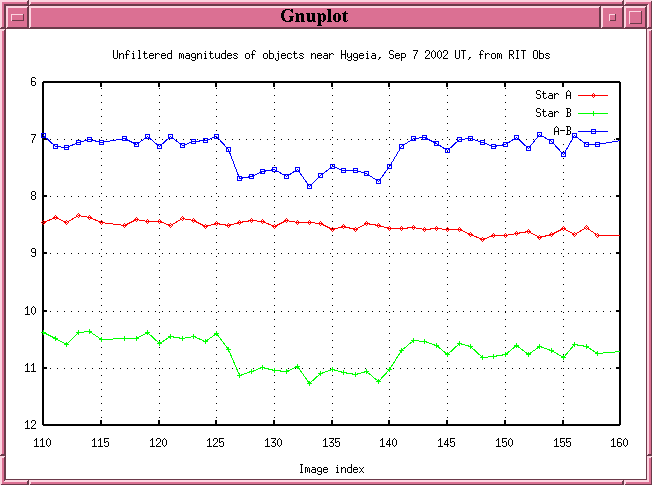
One example of the use of time in astronomy occurred here at RIT just a few years ago. Just after midnight on Friday, September 6, 2002, Prof. Tracy Davis and I watched as asteroid 10 Hygeia passed in front of a star.
Scientists used the orbit of the asteroid to predict that it would block the light of the star TYC 1244-00565-1 around midnight (EDT). They predicted that the shadow of the asteroid would move up the eastern coast of the US at a speed of about 2.96 km per second.
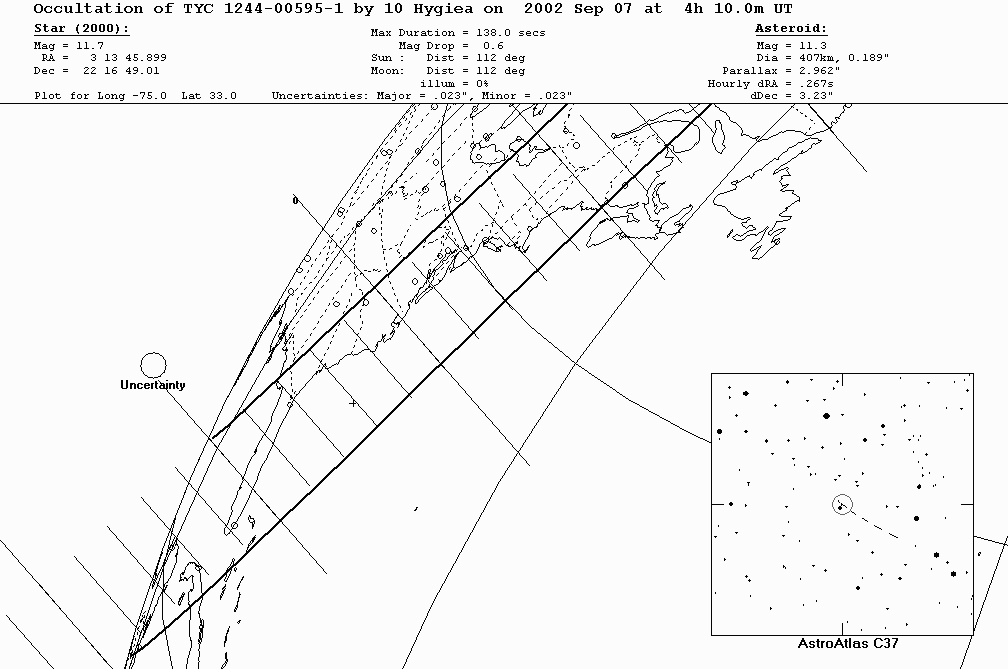
We used the RIT Observatory's 10-inch telescope

and CCD camera to take pictures of a very small area around the asteroid. The exposure time was just one second, and we were able to acquire one image every 5 seconds. Here's an example:
We took a series of about 200 images, starting at 11:52:48 PM. Astronomers had predicted that when the asteroid passed exactly in front of the star and blocked its light, the brightness of the star+asteroid would drop by about 50 percent. If you click on the image above, you'll see a short movie made from a sequence of our images near the predicted time of the event. Can you detect any changes in the brightness of the lower object?
It's easier to detect if you look at a graph of brightness versus time:
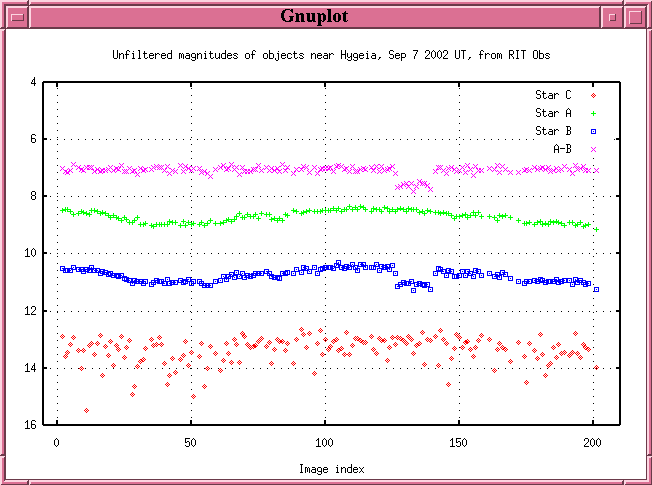
The graph below shows a closeup of the measurements made during the occultation. How large was the portion of asteroid Hygeia which passed over Rochester?
There will be another opportunity to observe the shadow of an asteroid from Rochester, this weekend! It will occur at about 1:00 AM on Saturday/Sunday night.
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.