Kinetic Energy of rotation

Do you remember what Kinetic Energy is, and how to calculate it?

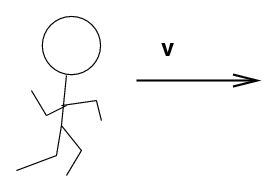
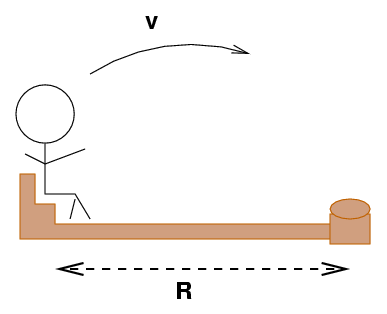
Jack is 150 cm tall and has a mass of 68 kg. He runs down the street at a speed of 7 m/s. What is Jack's kinetic energy?

What if the body in question is not TRANSLATING (moving in a straight line), but REVOLVING around some point? If you are given the linear velocity of the body, it's no different.

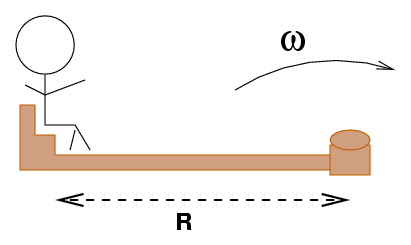
Jack is 150 cm tall and has a mass of 68 kg. He sits in the Whirl-a-Kid carnival ride, which has an arm of radius R = 3 m and spins him at a speed of 5 m/s. What is Jack's kinetic energy?

But what if you are given only the angular velocity?

Jack is 150 cm tall and has a mass of 68 kg. He sits in the Whirl-a-Kid carnival ride, which has an arm of radius R = 3 m and spins him at an angular speed of 0.5 revolutions per second. What is Jack's kinetic energy?

We can write the KE in terms of the angular velocity plus some other stuff ...

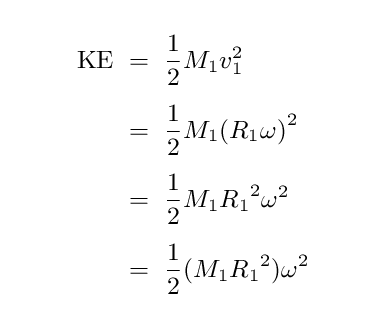
... but why should we bother?

The answer is -- if the rotating object is a complicated collection of pieces, then figuring out the linear velocity of each piece becomes tiresome.

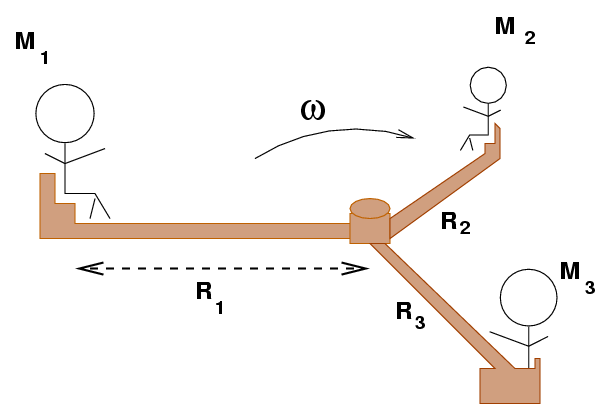
Jack has a mass of 68 kg, and sits R₁ = 3 m from the center of the ride. Fred has a mass of 55 kg, and sits R₂ = 2 m from the center of the ride. Bob has a mass of 73 kg, and sits R₂ = 4 m from the center of the ride. The Whirl-a-Kid spins at an angular speed of 0.5 revolutions per second. What is the total kinetic energy of the boys?

We can simplify the result down to a single, familiar-looking equation with just two variables

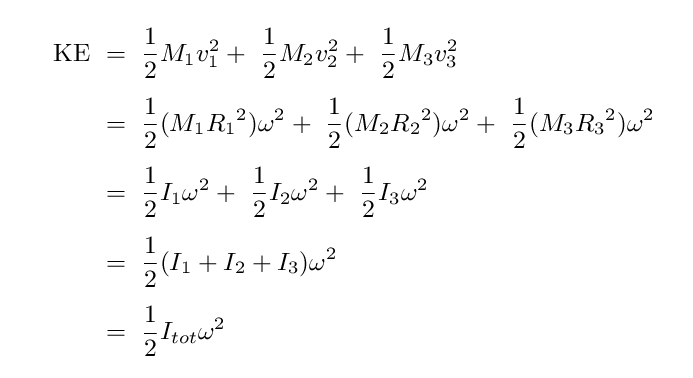
if we define a new quantity, the moment of inertia. For a compact mass, it is simply a combination of mass and distance-from-axis-of-rotation:

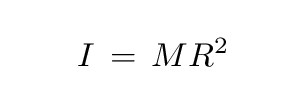
What IS this "moment of inertia"? You may recall that "inertia" is a fancy term which refers to the resistance of a body to a change in its motion. Items with large inertia -- like trucks and whales -- are hard to start moving, and hard to STOP moving once they get going. Items with small inertia -- like ping-pong balls and mice -- are easy to accelerate.

In a similar fashion, the "moment of inertia" measures the resistance of a body to a change in its rotation. A body with a large moment of inertia is hard to get spinning ... but, once it is spinning, is hard to stop. A body with a small moment of inertia is easy to start spinning, and easy to stop.