Analysis of the "swinging rings" experiment

You have a set of rings of different sizes:

You hang each ring from a pencil or pen and pull it gently to one side, then release it. The ring swings back and forth ...

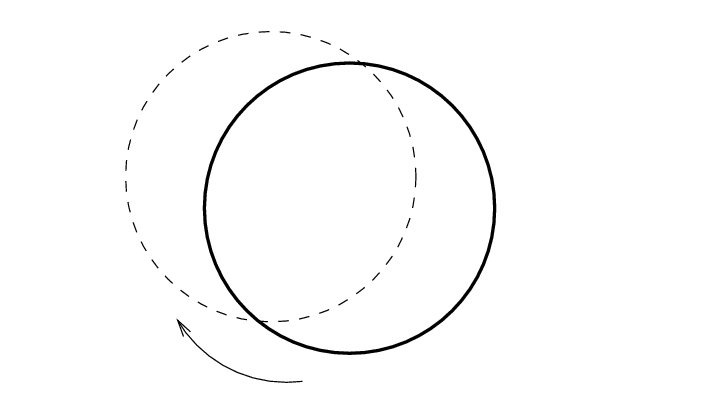
The goal is to figure out how long it would take a very large ring to complete one oscillation, based solely on the properties of the smaller rings.

Let's use this experiment to discuss some simple statistical notions, including the calculation of mean and standard deviation from the mean .

Describing the results of many measurements

I did this experiment, too. For a ring of diameter d = 7.7 cm, I measured the following times for 10 complete oscillations (that is, 10 back-and-forth swings).



  trial   1      5.46  sec
  trial   2      5.28  sec
  trial   3      5.29  sec

So, what can I conclude about the time it takes this ring to make 10 oscillations? If all the values were identical, I might say, "Aha, this ring takes exactly 5.46 seconds." But each trial was a little different.

In a case like this, when we have repeated measurements of what ought to be the same quantity, scientists often choose to describe the entire set of measurements with two numbers:

the mean is simply the average value.

We often use the Greek letter μ = "mu" to stand for the mean value. The mean is our best guess at the true value of the quantity -- the one we ought to measure, if we could use perfect instruments.

the standard deviation from the mean

We often use the Greek letter σ = "sigma" to stand for the standard deviation from the mean. The standard deviation is one way to describe the uncertainty in our guess at the true value.

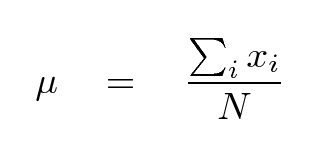
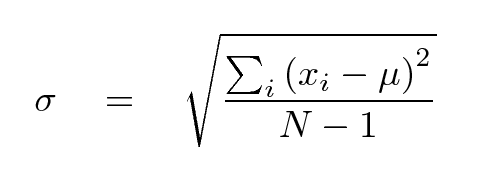
If you take a statistics class -- which would be a very good idea, at some point in your academic career -- you might learn about some of the delicate points that I've ignored in this brief introduction. For our purposes in this course, they aren't important.

Look again at my measurements. Can you compute the mean and standard deviation for the time it takes this ring to oscillate 10 times? Perhaps your calculator will do this for you ...



  trial   1      5.46  sec
  trial   2      5.28  sec
  trial   3      5.29  sec

Significant figures

Here are the results from my calculations.


 
    μ = 5.343  sec

    σ = 0.101 sec

Does this mean that we should write the following?

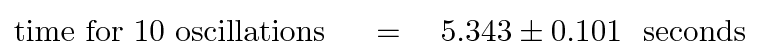
NO!

There are many possible values which lie within the stated uncertainty. Here are just a few:



   5.356   5.287   5.371   5.402   3.328   5.396   5.276   5.415

What do these values have in common?

They all start with a 5
Most follow with a .3

But the digit in the hundredth's place is pretty much random, as is the digit in the thousandth's place. It doesn't make sense to write a result which includes a digit in those places, because we really have no idea which digit it is.

So, let's get rid of all the "insignificant" digits -- the ones whose values we really don't know at all.

Oh, and if we remove those digits from the mean value, we should also remove the corresponding digits from the uncertainty.

So, the proper way to write the time it takes for the ring to make 10 oscillations is 5.3 +/- 0.1 seconds .

Your job: make a new table, in which you list the results of your own measurements. Compute the mean and standard deviation for each ring you measured, and write those values with the proper number of significant figures.

Graphs help to find relationships

We want to find the period of oscillation of a really big ring, but all we know are the periods for a set of small rings. What can we do?

find a relationship between period and diameter
use the known diameter of the big ring, and this relationship, to predict its period

For example, suppose that our measurements looked like this:



   diameter (cm)     period (s)
   -------------------------------
      5               1.0 
     10               2.0
     15               3.0
     20               4.0

   -------------------------------


   Q:  Can you predict the period of a ring of diameter 45 cm?

Well, sure. There's an obvious relationship, which we can express as an equation, like this:


                                                     1 s
          Period  (s)      =      Diameter (cm) *  ---------
                                                     5 cm

or as a graph, like this:



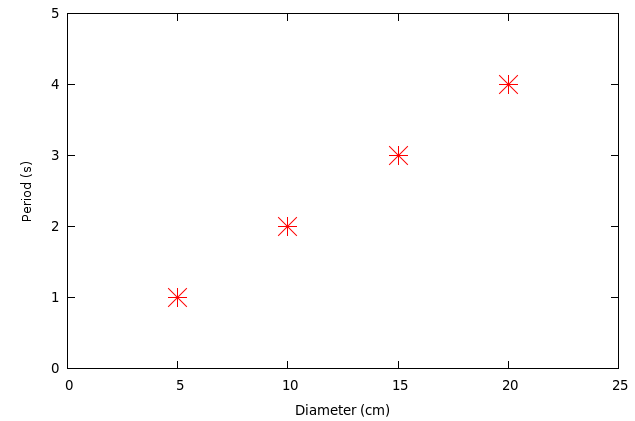
   Q:  What is the connection between the equation and the graph?