 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
SHM in action
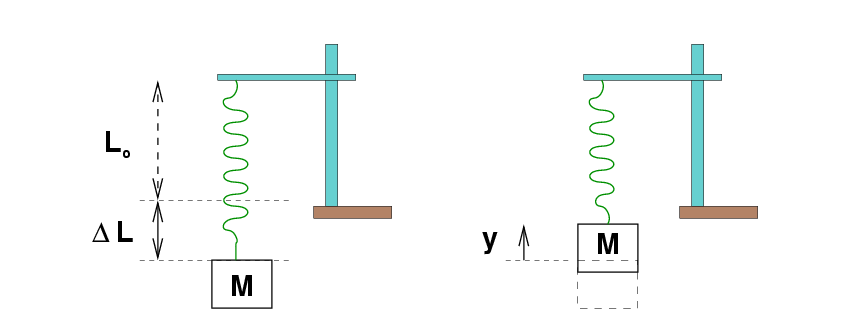
I have a spring of rest length Lo.
It hangs motionless from a horizontal rod.
When I hang a block of mass M
from the spring,
the spring grows longer by Δ L.
- Write an equation which shows all the
forces on the block in the vertical direction.
- What is the spring constant k of this spring?
Now, I grab the block and lift it up a small distance y
from the equilibrium position.
I then release it at time t = 0.
- Write an equation which shows all the forces on
the block in the vertical direction.
- Write Newton's Second Law for the block.
- Solve for the acceleration of the block in the vertical direction.
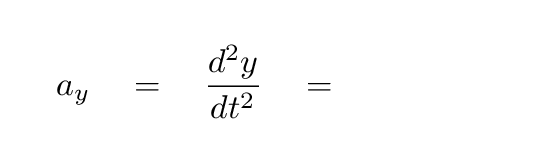
- Solve the differential equation, to find a function
which yields the y-position of the block as a function
of time in the following form:
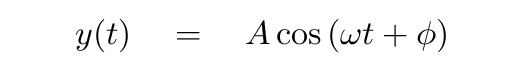
- What are the values of these parameters?
Include the units!
- Predict the time it should take for the
block to make one full cycle of oscillation
after I release it.
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
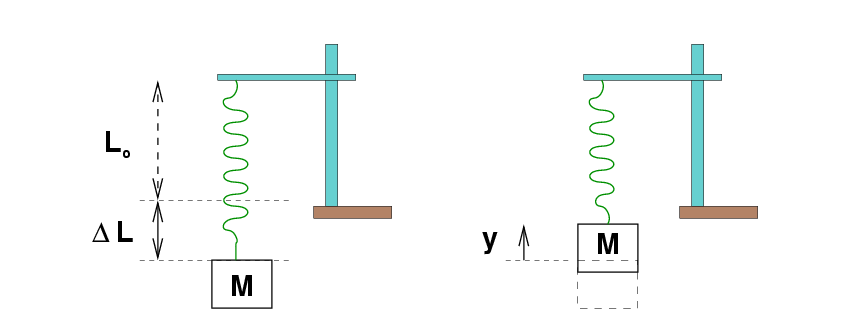
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
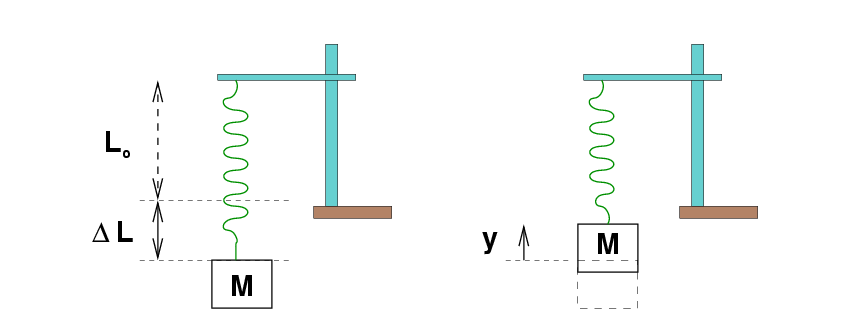
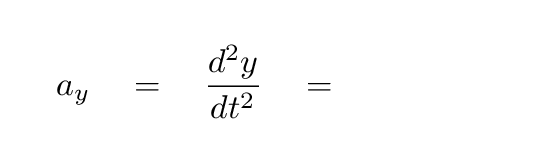
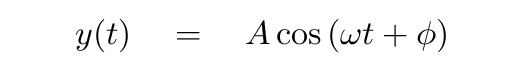
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.